Welcome!

class: center, middle, inverse, title-slide

# Welcome!
## An overview of the course
### Daniel Anderson
### Week 1

---

layout: true

---
# Agenda

.pull-left[

* Getting on the same page
* Syllabus
* A little bit of R
]

.pull-right[
![](edld629-logo.png)
]

---

# whoami

.pull-left[
* Research Assistant Professor: Behavioral Research and Teaching
* Dad (two daughters: 8 and 6)
* Pronouns: he/him/his
* Primary areas of interest: 💗💗R💗💗, computational research, achievement gaps, systemic inequities, and variance between educational institutions
]

.pull-right[

![](img/IMG_1306.jpeg)
]

---
background-image: url(https://media1.tenor.com/images/3589ebbb70e8e8de7e6170c16a6690d3/tenor.gif)
background-size: contain

---
class: center middle inverse-blue

# whoisyou?

.left[
* Introduce yourself

* Why are you here? I know you probs took HLM 1, but give me a little more than that.

* What pronouns would you like us to use for you for this class?

* What is one fun thing you have done not related to academic work recently?

* Do you have a furry friend you want to introduce?
]

---

# A few class policies

--
* Be kind

--
* Be understanding and have patience, with others and yourself

--
* Help others whenever possible

--
Truly the most important part of this class. Important not just in terms of decency, but also in your learning, and most importantly, for equity.

---
# A bit more specific

Normally I would have information here about welcoming kids into class.

Because we're virtual, that part is both easier and harder.

If you need to not attend class, or a portion of class, for any reason, that is fine.

Ideally you would let me know ahead of time. But we're in the middle of a pandemic and life is cray. Please .b[try] to contact me beforehand. If this isn't possible, please check in with me after.

---

# Last intro thing

* I'm here for you

* We won't have specific office hours, but know I'm always willing to meet

* This course, like all in the sequence, can be difficult. Don't suffer in silence. Don't do this alone.

---
class: inverse-green middle
background-size:cover

# Syllabus

---

# Course Website(s)

.pull-left[
## [website](https://mlm2-2021.netlify.app)
]

.pull-right[
.right[
## [repo](https://github.com/datalorax/mlm2)
  ]
]

---
# Materials
* Nearly everything will be distributed through the website. Go there now! Get the slides!

* If you feel comfortable, it would be best if you could clone the repo , then just pull each week for the most recent changes.

* We'll use Canvas for grading and announcements. I'll post a few things there too, but not much.

* The slides will always be available through the website, and you can click the button in the footer to download them as a PDF.

---
# A method by many names

All of these refer to the **same thing**!

* Hierarchical linear modeling

* Multilevel modeling

* Mixed effects modeling

--
And then there's a bunch of similar variants!

* Hierarchical linear regression

* Mixed effects regression

etc.

---
# The vocabulary I'll use
This class is technically called

.center[
**Hierarchical linear modeling II**.

I don't like that term

![](https://media0.giphy.com/media/l0MYzxkg0o1tkGSaI/source.gif)
]

---
# Multilevel modeling
Instead, I'll use the term multilevel modeling

* Keeps it distinct from hierarchical regression (not the same thing at all)

* Provides a useful heuristic

- Like many heuristics, can also be a bit limiting

---
# Course Learning objectives

* Fit and interpret multilevel models in R using both frequentist and Bayesian approaches

--
* Fit and interpret multilevel logistic regression models

--
* Visualize the fitted model predictions

--
* Understand the assumptions of multilevel models and be able to simulate data assuming the data were generated from a multilevel model

---
# Course Learning objectives

* Understand various variance-covariance specification of the random effects and how this relates to overfitting

--
* Understand and be able to translate equations between the Raudenbush & Bryk notation and the Gelman & Hill notation

--
* Be able to model growth flexibly within a multilevel framework, including discontinuous and non-linear trends

---
class: inverse-red middle
# A bit of a caveat
The previous two slides outline a lot of objectives.

My goal is to get you exposure to all of these concepts and help you dive deeper if you so choose

Not all learning objectives will be covered equally - this is an advanced class, you get to decide where you'd like to focus

---
# Weekly learning objectives

Provide you a frame for what you should be working to learn for that specific week.

### This week's objectives
* Understand the requirements of the course

* Understand the requirements of the final project

* Be ready to go with R and understand the basics of fitting a multilevel model

---
class: inverse-blue middle
# Textbooks

I will only require reading from textbooks that you can access for free.

---
# [Mixed models with R](https://m-clark.github.io/mixed-models-with-R/)

---
background-image: url(http://www.stat.columbia.edu/~gelman/arm/cover.gif)
background-position: right
class: middle

# [Gelman and hill](http://www.stat.columbia.edu/~gelman/arm/)
Not freely available but I will

provide select readings.

---

# Other books (also free)

.pull-left[
![](https://happygitwithr.com/img/watch-me-diff-watch-me-rebase-smaller.png)
## [Bryan](http://happygitwithr.com)
]

.pull-right[
.right[
<div>
<img src =https://d33wubrfki0l68.cloudfront.net/b88ef926a004b0fce72b2526b0b5c4413666a4cb/24a30/cover.png height = 400> 
</div>
  ]
]

.right[
### [Wickham & Grolemund](https://r4ds.had.co.nz)
]

---
background-image: url(https://images-na.ssl-images-amazon.com/images/I/511qSRzSlGL._SX338_BO1,204,203,200_.jpg)
background-position: right
class: middle

# One more
Not free, but recommended

---
class: inverse-red middle
# Assignments

## 100 points possible

---
# Participation (10%)

Each week, I'll ask you to follow along for specific parts of the slides.

You might also have notes you take on specific topics.

Please turn in your script and/or notes to canvas each week (1 point each).

Note - this is expected whether you attend "live" or watch the recording later.

---
# Homework

I am expecting we will have time to devote to the homework assignments in class.

You are welcome to work in groups.

Please use RMarkdown.

---
class: middle

### 15 points each (45 points total; 45%)

| Lab|Date Assigned |Date Due      |Topic                                                       |
|---:|:-------------|:-------------|:-----------------------------------------------------------|
|   1|Fri, April 09 |Fri, April 23 |Basic multilevel modeling with R                            |
|   2|Fri, April 23 |Fri, May 07   |Growth models and variance-covariance matrices              |
|   3|Fri, May 07   |Fri, May 21   |Bayesian estimation & multilevel logistic regression models |

---
# Final Project 
45 points total

### Three parts
* Proposal/outline (5 points): Due 4/30/21

* Script (20 points): Due 6/9/21

* Writeup (20 points): Due 6/9/21

---
# Proposal
### Four components

* Data source identified, which must be shareable with me

* Research Question(s) identified (no more than three), which must be 
  addressable through a multilevel model

* A description of any data processing that must occur before you can fit the 
  given model

* Your current status with the project (e.g., challenges you are facing,
  what steps still need to occur, feasibility of finishing, etc.)

---
# Script

See the [assignments](https://mlm2-2021.netlify.app/assignments/#r-script-20-points) page for full details

* Reproducibility: 2 points

* Exploratory and descriptive analyses: 3 points

* Analysis: 10 points
  + Model should map directly to the research question and be
    properly specified. 
  + Judgments are clear and justified from the evidence.

* Plots: 5 points
  + One plot **from your model** that communicates
    the coefficients, model predictions, or other features.

---
# Writeup

See the [assignments](https://mlm2-2021.netlify.app/assignments/#writeup-20-points) page for full details

**Must not** exceed five pages, double-spaced, w/standard margins and font size.

* Introduction: 2 points

* Research Question(s): 2 points

* Method: 5 points

* Results: 5 points

* Discussion: 3 points

* General style: 3 points

---
class: inverse-blue middle
# Grading

---
# Points
### 100 points total
* Participation (10 points total; one point per class)
* 3 Homework assignments at 15 points each (45 points) 
* Final project proposal/outline (5 points)
* Final project script (20 points)
* Final project writeup (20 points)

---

# Grading

|  **Lower percent** |**Lower point range**  | **Grade** | **Upper point range**  | **Upper percent**|
|  :------: | :------  | :-:| :------: | ----:|
|  0.97     | (97 pts) | A+ |          |      |
|  0.93     | (93 pts) | A  | (97 pts) | 0.97 |
|  0.90     | (90 pts) | A- | (93 pts) | 0.93 |
|  0.87     | (87 pts) | B+ | (90 pts) | 0.90 |
|  0.83     | (83 pts) | B  | (87 pts) | 0.87 |
|  0.80     | (80 pts) | B- | (83 pts) | 0.83 |
|  0.77     | (77 pts) | C+ | (80 pts) | 0.80 |
|  0.73     | (73 pts) | C  | (77 pts) | 0.77 |
|  0.70     | (70 pts) | C- | (73 pts) | 0.73 |
|           |          | F  | (69 pts < ) | 0.70 |

---
# A note on deadlines

Life be cray - don't worry about any deadlines except the final project, and make sure you get all assignments in by the final.

Do worry about the final project deadline - it can't be moved. I'd suggest starting on it ASAP. You can turn things like your proposal in anytime.

---
class: inverse
background-image:url(https://d194ip2226q57d.cloudfront.net/original_images/10_Tips_for_Workplace_Communication)
background-size:contain

---
# A few final notes
* This is the first time I've taught this course

* I don't have a great feel for how long things will take

* Please be patient with me if we end up needing to make some changes to the course schedule

* I do plan on this being highly applied, with you running lots of models and playing with data immediately

---
# My approach
The first basically half of the quarter will be on

* Moving to R

* Deepening your current understanding

--
This means that for many of you, there probably won't be a lot of completely "new" content at first (e.g., Bayesian approaches)

--
That will come, but I want to focus on depth of understanding first

---
# Differentiation
* I know most of you, but not all

* Please understand that there is a wide range of comfort levels in this class both with R and multilevel model

+ Occasionally it may feel slow, or way too fast
  + Please be patient in either case, but **do** speak up if you are feeling lost - formative feedback is much more difficult through zoom and I may not know I'm losing you if you don't speak up.

---
class: inverse-red
# Final note
This is a long class - we'll try to take at least one 5-minute break each time

---
class: inverse
background-image:url(https://images.pexels.com/photos/1887995/pexels-photo-1887995.jpeg?auto=compress&cs=tinysrgb&dpr=2&h=650&w=940)
background-size:contain

---
class: inverse-red middle

# My assumptions about you

---
# I assume you

* Have a strong foundational knowledge of multiple regression

+ Example: You can interpret two-way interactions without twisting your brain too much

--
* Understand how multilevel modeling extends the basic multiple regression model

--
* Can correctly interpret two- and three-level models

--
* Have at least a basic understanding of how multilevel modeling can be used to estimate change over time

---
# Pop quiz

In groups, discuss each of the following, then we'll discuss as a class:

* When is multilevel modeling preferred. Is it always better that multiple regression?
* What does it mean for something to be **nested**. Can multilevel modeling be used if the data are not nested?
* Describe the differences between multiple regression and a model with 
  - Random intercepts
  - Random slopes
  - Random intercepts and slopes
* Why does multilevel modeling allow you to investigate changes over time? What specifically makes it different?

---

---
# Pop Quiz #2

Describe the model below in plain words.

$$
`\begin{aligned}
\text{math}_{ijk} &= \pi_{0jk} + \pi_{1jk}(week) + e_{ijk} \\\
\pi_{0jk} &= \beta_{00k} + \beta_{01k}(FRL) + r_{0jk} \\\
\pi_{1jk} &= \beta_{10k} + \beta_{11k}(FRL) + r_{1jk} \\\
\beta_{00k} &= \gamma_{000} + \gamma_{001}(Size) + u_{00k} \\\
\beta_{01k} &= \gamma_{010} + \gamma_{011}(Size) + u_{01k} \\\
\beta_{10k} &= \gamma_{100} + \gamma_{101}(Size) + u_{10k} \\\
\beta_{11k} &= \gamma_{110} 
\end{aligned}`
$$
where `$i$`, `$j$`, and `$k$` index time points, students, and schools; `$FRL$` is free/reduced lunch eligibility, and `$Size$` is the school size

---

---
# Fixed effects
The model on the previous slide estimates:

--
* the relation between time and students' math scores in weekly units, `$\gamma_{1000}$`

- .gray[Each week students gained, on average, X math points]

--
* the relation between FRL eligibility and students' initial math scores, `$\gamma_{010}$`, and their weekly rate of growth, `$\gamma_{110}$` .gray[(cross-level interaction)]

--
* the relation between school size and students' initial math achievement, `$\gamma_{001}$`, rate of growth, `$\gamma_{101}$`, and the school-size relation with student-level FRL eligibility on initial achievement, `$\gamma_{011}$` .gray[(cross-level interaction)]

---
# Random effects
It also estimates:

--
* Between-student variability in initial math scores, `$r_{0jk}$` and rate of weekly change, `$r_{1jk}$`, *as well as their covariance .gray[(not shown)]*

--
* Between-school variability in initial math scores, `$u_{00k}$`, rate of weekly change, `$u_{10k}$`, and the relation between student FRL eligibility and initial achievement, `$u_{10k}$`, *as well as all covariances .gray[(not shown)]*

---
# Back to assumptions
### Related to R: I assume you

* Have a basic understanding of the R package ecosystem (how to find, install, load, and learn about them)

--
* Can read "flat" (i.e., rectangular) datasets into R

--
* Know and use RStudio Projects & the [{here}](https://github.com/r-lib/here) package

- See [Jenny Bryan's blog post](https://www.tidyverse.org/articles/2017/12/workflow-vs-script/) for why.

---
* Can perform basic data wrangling and transformations in R, using the
tidyverse

+ Leverage appropriate functions for introductory data science tasks (pipeline)
  + "clean up" the dataset using scripts and reproducible workflows

--
* Use R Markdown to create at least basic reproducible and dynamic documents

---
class: inverse-blue bottom
background-image:url(https://3.bp.blogspot.com/-UvxqmChbel4/Tm7C2hlrc3I/AAAAAAAADMQ/FJMAlVF_dtE/s1600/CAPITAL-LETTER-R.png)
background-size:contain

# Let's go!

---
# Let's play with R
* Open RStudio
* Install any of the packages below you don't already have installed

* General recommendation when installing packages - Type 1 at prompt to update old packages - select "no" if asked to compile from source

```r
install.package("tidyverse")
install.packages("lme4")
install.packages("equatiomatic")
remotes::install_github("easystats/easystats")

# Or for the latest and greatest features for equatiomatic
remotes::install_github("datalorax/equatiomatic")
```

---
Load **equatiomatic** and you should have access to the `hsb` dataset

```r
library(equatiomatic)
head(hsb)
```

```
##   sch.id   math size sector meanses minority female    ses
## 1   1224  5.876  842      0  -0.428        0      1 -1.528
## 2   1224 19.708  842      0  -0.428        0      1 -0.588
## 3   1224 20.349  842      0  -0.428        0      0 -0.528
## 4   1224  8.781  842      0  -0.428        0      0 -0.668
## 5   1224 17.898  842      0  -0.428        0      0 -0.158
## 6   1224  4.583  842      0  -0.428        0      0  0.022
```

---
# HSB
* I'm assuming you're all familiar with it. Perhaps painfully so.

* We're just doing some basic R stuff here

* Let's load the **tidyverse** and compute:
  + mean math scores by school
  + standard error of the mean, which is `$\frac{\sigma}{\sqrt{n}}$`

---

```r
library(tidyverse)
sch_means <- hsb %>% 
  group_by(sch.id) %>% 
  summarize(sch_mean = mean(math, na.rm = TRUE),
            sch_mean_se = sd(math, na.rm = TRUE)/sqrt(n()))
sch_means
```

```
## # A tibble: 160 x 3
##    sch.id  sch_mean sch_mean_se
##     <int>     <dbl>       <dbl>
##  1   1224  9.715447   1.107521 
##  2   1288 13.5108     1.404369 
##  3   1296  7.635958   0.7723605
##  4   1308 16.2555     1.367186 
##  5   1317 13.17769    0.7884564
##  6   1358 11.20623    1.072893 
##  7   1374  9.728464   1.579465 
##  8   1433 19.71914    0.6551441
##  9   1436 18.11161    0.6856883
## 10   1461 16.84264    1.209306 
## # … with 150 more rows
```

---
# Plot the means by school

Not particularly helpful

```r
ggplot(sch_means, aes(sch_mean, sch.id)) +
  geom_point()
```

![](w1p1_files/figure-html/unnamed-chunk-10-1.png)

---
# Order schools

```r
sch_means %>% 
* mutate(sch.id = factor(sch.id),
*        sch.id = reorder(sch.id, sch_mean)) %>%
  ggplot(aes(sch_mean, sch.id)) +
  geom_point()
```

![](w1p1_files/figure-html/unnamed-chunk-11-1.png)

---
# Add SE of mean

```r
sch_means %>% 
  mutate(sch.id = factor(sch.id),
         sch.id = reorder(sch.id, sch_mean)) %>% 
  ggplot(aes(sch_mean, sch.id)) +
* geom_errorbarh(
*   aes(xmin = sch_mean - 1.96*sch_mean_se,
*       xmax = sch_mean + 1.96*sch_mean_se),
* ) +
  geom_point(color = "#0aadff")
```

---
# Add SE of mean

![](w1p1_files/figure-html/unnamed-chunk-13-1.png)

---
# Add sample mean

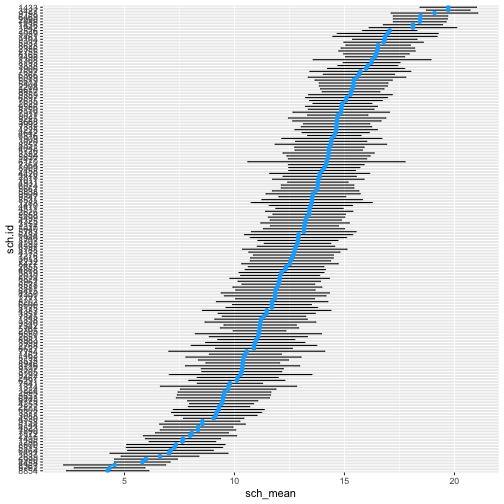
```r
sch_means %>% 
  mutate(sch.id = factor(sch.id),
         sch.id = reorder(sch.id, sch_mean)) %>% 
  ggplot(aes(sch_mean, sch.id)) +
  geom_errorbarh(
    aes(xmin = sch_mean - 1.96*sch_mean_se,
        xmax = sch_mean + 1.96*sch_mean_se),
    height = 0.3
  ) + 
  geom_point(color = "#0aadff") +
* geom_vline(xintercept = mean(hsb$math, na.rm = TRUE),
*            color = "#0affa5",
*            size = 2)
```

---
# Add sample mean

![](w1p1_files/figure-html/unnamed-chunk-15-1.png)

---
# Why did we do this?
We could make the prior plot prettier, but that's not really why we were doing this.

--
Do you think there's between-school variation in math scores?

--
Let's model it!

---
# Fit a basic model

```r
# install.packages("lme4")
library(lme4)
```

--
Can we fit a model equivalent to what we just did descriptively?

What would that look like? (I don't mean code, I mean statistically/conceptually)

---
# Unconditional model
An unconditional model just estimates a mean score for each school.

--
If we have no other variables in our model, the prediction for each student would equal the school mean

--
Using the Gelman and Hill notation, the unconditional model we want would look like this:

$$
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i]}, \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right)
    \text{, for sch.id j = 1,} \dots \text{,J}
\end{aligned}`
$$

which we'll get into more later.

---
# Estimate it!
When we use **lme4** to estimate this model, it looks like this:

```r
m0 <- lmer(math ~ 1 + (1|sch.id), hsb)
```

--
We learn more about this model with `summary(m0)`.

--
If you're used to the HLM software, this will seem *blazingly* fast.

---

```r
summary(m0)
```

```
## Linear mixed model fit by REML ['lmerMod']
## Formula: math ~ 1 + (1 | sch.id)
##    Data: hsb
## 
## REML criterion at convergence: 47116.8
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0631 -0.7539  0.0267  0.7606  2.7426 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sch.id   (Intercept)  8.614   2.935   
##  Residual             39.148   6.257   
## Number of obs: 7185, groups:  sch.id, 160
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  12.6370     0.2444   51.71
```

---
# In equation form
$$
`\begin{aligned}
  \operatorname{\widehat{math}}_{i}  &\sim N \left(12.64_{\alpha_{j[i]}}, \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(0, 2.93 \right)
    \text{, for sch.id j = 1,} \dots \text{,J}
\end{aligned}`
$$

--
Part of why I like the above notation more is that it makes our assumptions explicit

--
What's your guess - how will our model-estimated school means compare to our descriptive stats?

---
# Pull estimated means
We won't worry about the standard errors for now.

```r
estimated_means <- coef(m0)$sch.id
head(estimated_means)
```

```
##      (Intercept)
## 1224    9.973039
## 1288   13.376384
## 1296    8.068508
## 1308   15.585491
## 1317   13.130920
## 1358   11.394462
```

---
# Join them

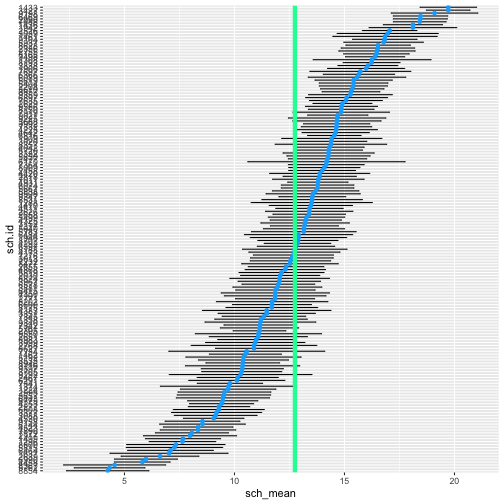
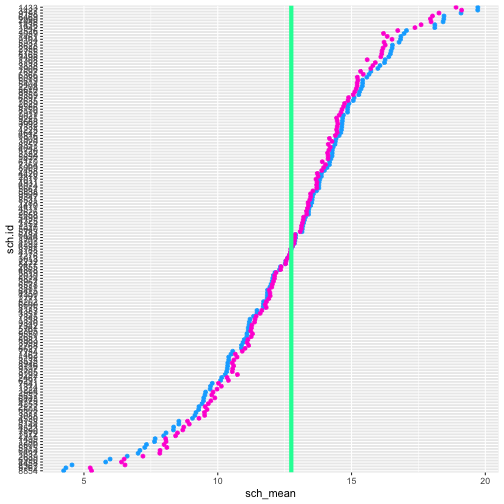
```r
estimated_means <- estimated_means %>% 
  mutate(sch.id = as.integer(rownames(.))) %>% 
  rename(intercept = `(Intercept)`)

left_join(sch_means, estimated_means)
```

```
## Joining, by = "sch.id"
```

```
## # A tibble: 160 x 4
##    sch.id  sch_mean sch_mean_se intercept
##     <int>     <dbl>       <dbl>     <dbl>
##  1   1224  9.715447   1.107521   9.973039
##  2   1288 13.5108     1.404369  13.37638 
##  3   1296  7.635958   0.7723605  8.068508
##  4   1308 16.2555     1.367186  15.58549 
##  5   1317 13.17769    0.7884564 13.13092 
##  6   1358 11.20623    1.072893  11.39446 
##  7   1374  9.728464   1.579465  10.13462 
##  8   1433 19.71914    0.6551441 18.90522 
##  9   1436 18.11161    0.6856883 17.59908 
## 10   1461 16.84264    1.209306  16.33355 
## # … with 150 more rows
```

---
# Plot it

```r
left_join(sch_means, estimated_means) %>% 
  mutate(sch.id = factor(sch.id),
         sch.id = reorder(sch.id, sch_mean)) %>% 
  ggplot(aes(sch_mean, sch.id)) +
  geom_point(color = "#0aadff") +
  geom_point(aes(x = intercept),
             color = "#ff0ad6") +
    geom_vline(xintercept = mean(hsb$math, na.rm = TRUE),
             color = "#0affa5",
             size = 2)
```

---
class: center

![](w1p1_files/figure-html/unnamed-chunk-24-1.png)

Points are being pulled toward the grand mean

---
# ICC

* We can estimate the ICC with the **performance** package
* Part of **easystats**

```r
library(performance)
icc(m0)
```

```
## # Intraclass Correlation Coefficient
## 
##      Adjusted ICC: 0.180
##   Conditional ICC: 0.180
```

So approximately 18% of the variability in math scores lies between schools.

---
class: inverse-green middle
# Next time
* Data structuring - moving data to a longer format
* Random intercepts, random slopes, multiple levels
* Homework 1 is assigned - we'll hopefully have 30-45 minutes to work on it in class.