Agenda

• Restructuring data

• Fitting models:

  • Unconditional model
  • Random intercepts
  • Random slopes

• Homework 1

Learning objectives

• Understand the basics of moving data from a wider form to a longer form

• Understand the basics of the lme4::lmer() syntax

Today will be highly applied, and (I hope) mostly review

The only real difference is it will be in R

Schedule announcement

• I've moved back when Homework 2 and 3 are assigned by one week

• I felt like this worked better with the topics (gave us more time for variance-covariance matrices and intro to Bayes)

• Now assigned weeks 5 & 7, and due weeks 7 & 9

First, load the data

library(tidyverse)
curran <- read_csv(here::here("data", "curran.csv"))
curranCopy Code

## # A tibble: 405 x 15
##       id anti1 anti2 anti3 anti4 read1 read2 read3 read4 kidgen momage kidage
##    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>  <dbl>  <dbl>
##  1    22     1     2    NA    NA   2.1   3.9  NA    NA        0     28   6.08
##  2    34     3     6     4     5   2.1   2.9   4.5   4.5      1     28   6.83
##  3    58     0     2     0     1   2.3   4.5   4.2   4.6      0     28   6.5 
##  4   122     0     3     1     1   3.7   8    NA    NA        1     28   7.83
##  5   125     1     1     2     1   2.3   3.8   4.3   6.2      0     29   7.42
##  6   133     3     4     3     5   1.8   2.6   4.1   4        1     28   6.75
##  7   163     5     4     5     5   3.5   4.8   5.8   7.5      1     28   7.17
##  8   190     0    NA    NA     0   2.9   6.1  NA    NA        0     28   6.67
##  9   227     0     0     2     1   1.8   3.8   4    NA        0     29   6.25
## 10   248     1     2     2     0   3.5   5.7   7     6.9      0     28   7.5 
## # … with 395 more rows, and 3 more variables: homecog <dbl>, homeemo <dbl>,
## #   nmis <dbl>Copy Code

About the data

The data are a sample of 405 children who were within the first two years of entry to elementary school. The data consist of four repeated measures of both the child’s antisocial behavior and the child’s reading recognition skills. In addition, on the first measurement occasion, measures were collected of emotional support and cognitive stimulation provided by the mother. The data were collected using face-to-face interviews of both the child and the mother at two-year intervals between 1986 and 1992.

See here

Format

• Let's say we want to use reading scores as the outcome

• We have four columns of reading scores

• We can't specify multiple outcomes.

What do we do?

Make the data longer

Image from R for Data Science

Let's start easy

First, let's select just the ID variable and the reading scores

read <- curran %>% 
  select(id, starts_with("read"))
readCopy Code

## # A tibble: 405 x 5
##       id read1 read2 read3 read4
##    <dbl> <dbl> <dbl> <dbl> <dbl>
##  1    22   2.1   3.9  NA    NA  
##  2    34   2.1   2.9   4.5   4.5
##  3    58   2.3   4.5   4.2   4.6
##  4   122   3.7   8    NA    NA  
##  5   125   2.3   3.8   4.3   6.2
##  6   133   1.8   2.6   4.1   4  
##  7   163   3.5   4.8   5.8   7.5
##  8   190   2.9   6.1  NA    NA  
##  9   227   1.8   3.8   4    NA  
## 10   248   3.5   5.7   7     6.9
## # … with 395 more rowsCopy Code

What should our data look like?

• Take two minutes to visualize what you think the data should look like

• Feel free to even sketch something out.

• We'll talk about it as a class after

Moving to longer

read %>% 
  pivot_longer(cols = read1:read4,
               names_to = "timepoint",
               values_to = "score")Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl> <chr>     <dbl>
##  1    22 read1       2.1
##  2    22 read2       3.9
##  3    22 read3      NA  
##  4    22 read4      NA  
##  5    34 read1       2.1
##  6    34 read2       2.9
##  7    34 read3       4.5
##  8    34 read4       4.5
##  9    58 read1       2.3
## 10    58 read2       4.5
## # … with 1,610 more rowsCopy Code

Alternative

You can also specify the columns that should not be pivoted

read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score")Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl> <chr>     <dbl>
##  1    22 read1       2.1
##  2    22 read2       3.9
##  3    22 read3      NA  
##  4    22 read4      NA  
##  5    34 read1       2.1
##  6    34 read2       2.9
##  7    34 read3       4.5
##  8    34 read4       4.5
##  9    58 read1       2.3
## 10    58 read2       4.5
## # … with 1,610 more rowsCopy Code

Are we done?

• In this case, we probably want to fit a growth model. That means timepoint needs to be numeric.

• There are numerous ways to do this - here are a few

Mutate

• Use mutate() to modify the column afterwords

Why did I subtract 1?

read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score") %>% 
  mutate(timepoint = parse_number(timepoint) - 1)Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl>     <dbl> <dbl>
##  1    22         0   2.1
##  2    22         1   3.9
##  3    22         2  NA  
##  4    22         3  NA  
##  5    34         0   2.1
##  6    34         1   2.9
##  7    34         2   4.5
##  8    34         3   4.5
##  9    58         0   2.3
## 10    58         1   4.5
## # … with 1,610 more rowsCopy Code

Transform during the pivot

read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score",
               names_transform = list(
                 timepoint = parse_number)
               )Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl>     <dbl> <dbl>
##  1    22         1   2.1
##  2    22         2   3.9
##  3    22         3  NA  
##  4    22         4  NA  
##  5    34         1   2.1
##  6    34         2   2.9
##  7    34         3   4.5
##  8    34         4   4.5
##  9    58         1   2.3
## 10    58         2   4.5
## # … with 1,610 more rowsCopy Code

Alternative transformation

This does the subtraction by 1 also

sub1 <- function(x) parse_number(x) - 1
read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score",
               names_transform = list(timepoint = sub1))Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl>     <dbl> <dbl>
##  1    22         0   2.1
##  2    22         1   3.9
##  3    22         2  NA  
##  4    22         3  NA  
##  5    34         0   2.1
##  6    34         1   2.9
##  7    34         2   4.5
##  8    34         3   4.5
##  9    58         0   2.3
## 10    58         1   4.5
## # … with 1,610 more rowsCopy Code

Yet another approach

This one doesn't subtract 1, however

read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score",
               names_prefix = "read",
               names_ptype = list(timepoint = "numeric"))Copy Code

## # A tibble: 1,620 x 3
##       id timepoint score
##    <dbl> <chr>     <dbl>
##  1    22 1           2.1
##  2    22 2           3.9
##  3    22 3          NA  
##  4    22 4          NA  
##  5    34 1           2.1
##  6    34 2           2.9
##  7    34 3           4.5
##  8    34 4           4.5
##  9    58 1           2.3
## 10    58 2           4.5
## # … with 1,610 more rowsCopy Code

Moving back

Although moving longer is most often useful for multilevel modeling, occasionally we need to go wider - e.g., for a join.

First, let's create a longer data object

l <- read %>% 
  pivot_longer(-id,
               names_to = "timepoint",
               values_to = "score",
               names_transform = list(timepoint = sub1))Copy Code

Now let's move it back

Use pivot_wider() instead

l %>% 
  pivot_wider(names_from = timepoint, 
              values_from = score)Copy Code

## # A tibble: 405 x 5
##       id   `0`   `1`   `2`   `3`
##    <dbl> <dbl> <dbl> <dbl> <dbl>
##  1    22   2.1   3.9  NA    NA  
##  2    34   2.1   2.9   4.5   4.5
##  3    58   2.3   4.5   4.2   4.6
##  4   122   3.7   8    NA    NA  
##  5   125   2.3   3.8   4.3   6.2
##  6   133   1.8   2.6   4.1   4  
##  7   163   3.5   4.8   5.8   7.5
##  8   190   2.9   6.1  NA    NA  
##  9   227   1.8   3.8   4    NA  
## 10   248   3.5   5.7   7     6.9
## # … with 395 more rowsCopy Code

Challenge

Let's go back to the full curran data. See if you can get your data to look like the below.

There are, again, multiple ways to do this, including only through pivot_longer

## # A tibble: 3,240 x 10
##       id kidgen momage kidage homecog homeemo  nmis variable timepoint value
##    <dbl>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl> <dbl> <chr>        <dbl> <dbl>
##  1    22      0     28   6.08      13      10     4 anti             0   1  
##  2    22      0     28   6.08      13      10     4 anti             1   2  
##  3    22      0     28   6.08      13      10     4 anti             2  NA  
##  4    22      0     28   6.08      13      10     4 anti             3  NA  
##  5    22      0     28   6.08      13      10     4 read             0   2.1
##  6    22      0     28   6.08      13      10     4 read             1   3.9
##  7    22      0     28   6.08      13      10     4 read             2  NA  
##  8    22      0     28   6.08      13      10     4 read             3  NA  
##  9    34      1     28   6.83       9       9     0 anti             0   3  
## 10    34      1     28   6.83       9       9     0 anti             1   6  
## # … with 3,230 more rowsCopy Code

More transforming

Our data is probably still not in the format we want. Can you get it in the format like the below?

## # A tibble: 1,620 x 10
##       id kidgen momage kidage homecog homeemo  nmis timepoint  anti  read
##    <dbl>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl> <dbl>     <dbl> <dbl> <dbl>
##  1    22      0     28   6.08      13      10     4         0     1   2.1
##  2    22      0     28   6.08      13      10     4         1     2   3.9
##  3    22      0     28   6.08      13      10     4         2    NA  NA  
##  4    22      0     28   6.08      13      10     4         3    NA  NA  
##  5    34      1     28   6.83       9       9     0         0     3   2.1
##  6    34      1     28   6.83       9       9     0         1     6   2.9
##  7    34      1     28   6.83       9       9     0         2     4   4.5
##  8    34      1     28   6.83       9       9     0         3     5   4.5
##  9    58      0     28   6.5        9       6     0         0     0   2.3
## 10    58      0     28   6.5        9       6     0         1     2   4.5
## # … with 1,610 more rowsCopy Code

Another example

Read in the letter sounds data

ls <- read_csv(here::here("data", "ls19.csv"))
lsCopy Code

## # A tibble: 962 x 13
##    county       distid dist_name          instid inst_name          inst_type
##    <chr>         <dbl> <chr>               <dbl> <chr>              <chr>    
##  1 All Counties   9999 Statewide            9999 Statewide          State    
##  2 Baker          1894 Baker SD 5J          1894 Baker SD 5J        District 
##  3 Baker          1895 Huntington SD 16J    1895 Huntington SD 16J  District 
##  4 Baker          1896 Burnt River SD 30J   1896 Burnt River SD 30J District 
##  5 Baker          1897 Pine Eagle SD 61     1897 Pine Eagle SD 61   District 
##  6 Benton         1898 Monroe SD 1J         1898 Monroe SD 1J       District 
##  7 Benton         1899 Alsea SD 7J          1899 Alsea SD 7J        District 
##  8 Benton         1900 Philomath SD 17J     1900 Philomath SD 17J   District 
##  9 Benton         1901 Corvallis SD 509J    1901 Corvallis SD 509J  District 
## 10 Clackamas      1902 Clackamas ESD        1902 Clackamas ESD      District 
## # … with 952 more rows, and 7 more variables: asian <dbl>,
## #   black_african_american <dbl>, hispanic_latino <dbl>,
## #   american_indian_alaska_native <dbl>, multi_racial <dbl>,
## #   native_hawaiian_pacific_islander <dbl>, white <dbl>Copy Code

LS Data

• Average scores on the letter sounds portion of the kindergarten entry assessment for every school in the state, by race.

• Data missing if n too small

• Remember - you (generally) don't need to dummy-code variables in R

• Try structuring this data so you could estimate between-district variability, while accounting for race/ethnicity

Self-regulation data

• Same basic data with a different outcome and a different structure.

• Try restructuring this one

selfreg <- read_csv(here::here("data", "selfreg19.csv"))
selfregCopy Code

## # A tibble: 6,734 x 13
##    county       distid dist_name   instid inst_name   inst_type selfreg_score
##    <chr>         <dbl> <chr>        <dbl> <chr>       <chr>             <dbl>
##  1 All Counties   9999 Statewide     9999 Statewide   State               3.7
##  2 All Counties   9999 Statewide     9999 Statewide   State               3.3
##  3 All Counties   9999 Statewide     9999 Statewide   State               3.4
##  4 All Counties   9999 Statewide     9999 Statewide   State               3.3
##  5 All Counties   9999 Statewide     9999 Statewide   State               3.5
##  6 All Counties   9999 Statewide     9999 Statewide   State               3.4
##  7 All Counties   9999 Statewide     9999 Statewide   State               3.5
##  8 Baker          1894 Baker SD 5J   1894 Baker SD 5J District           NA  
##  9 Baker          1894 Baker SD 5J   1894 Baker SD 5J District           NA  
## 10 Baker          1894 Baker SD 5J   1894 Baker SD 5J District            3.9
## # … with 6,724 more rows, and 6 more variables: Asian <dbl>,
## #   Black.African.American <dbl>, Hispanic.Latino <dbl>, Multi.Racial <dbl>,
## #   Native.Hawaiian.Pacific.Islander <dbl>, White <dbl>Copy Code

A bit of a caveat

• The preceding examples would lead to sort of fundamentally flawed analyses

• We'd be estimating each district mean as the mean of the school means

• There are ways to account for this, which we may or may not get into later in the term

• Could potentially try weighting each school mean by the school size

Back to curran data

• Let's fit a basic two-level growth model

• We'll compare a random intercepts model to a random slopes model and talk about some of the complexities involved

Model fitting

• We could start with a fully unconditional model (not unconditional growth), but that's really a misspecification in this case - we know we have to account for time.

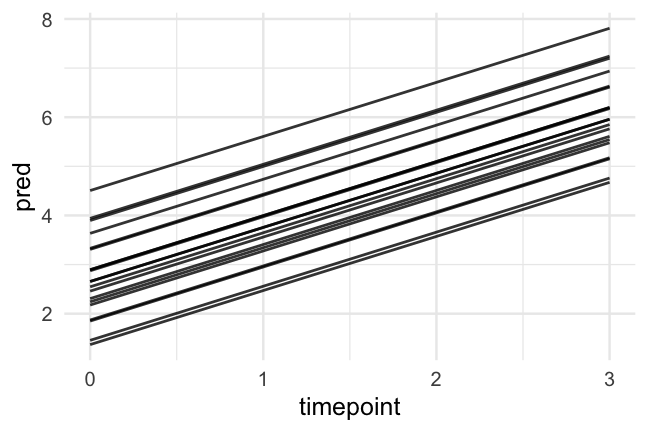
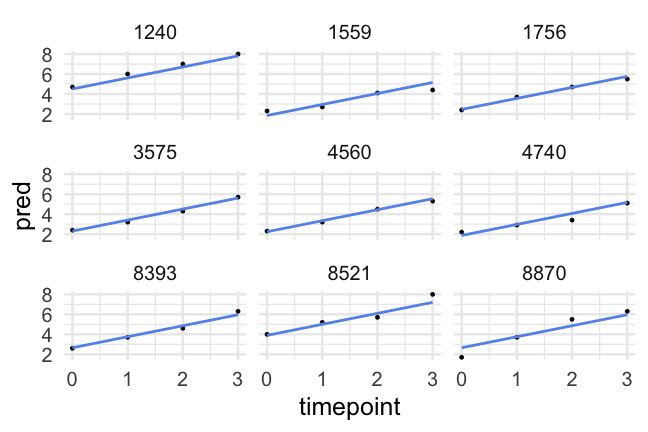
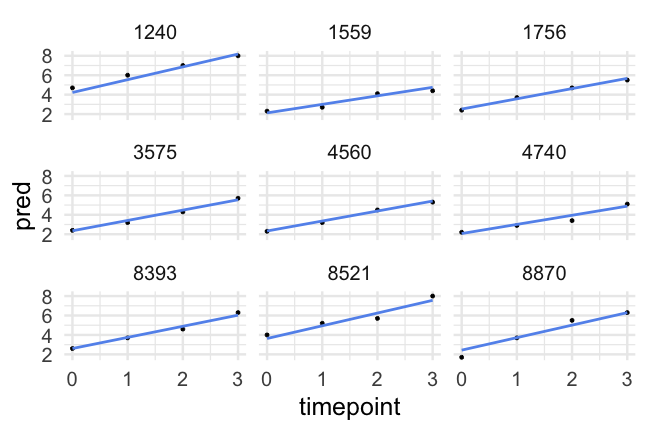
• Let's first fit a model with random intercepts

• A reminder of what the data look like

dCopy Code

## # A tibble: 1,620 x 10
##       id kidgen momage kidage homecog homeemo  nmis timepoint  anti  read
##    <dbl>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl> <dbl>     <dbl> <dbl> <dbl>
##  1    22      0     28   6.08      13      10     4         0     1   2.1
##  2    22      0     28   6.08      13      10     4         1     2   3.9
##  3    22      0     28   6.08      13      10     4         2    NA  NA  
##  4    22      0     28   6.08      13      10     4         3    NA  NA  
##  5    34      1     28   6.83       9       9     0         0     3   2.1
##  6    34      1     28   6.83       9       9     0         1     6   2.9
##  7    34      1     28   6.83       9       9     0         2     4   4.5
##  8    34      1     28   6.83       9       9     0         3     5   4.5
##  9    58      0     28   6.5        9       6     0         0     0   2.3
## 10    58      0     28   6.5        9       6     0         1     2   4.5
## # … with 1,610 more rowsCopy Code

Fit the model

Let's talk through what's going on here:

library(lme4)
m_intercepts <- lmer(read ~ 1 + timepoint + (1|id),
                     data = d)Copy Code

Notation

Raudenbush and Bryk

$$\begin{array}{cc}{\text{read}}_{ij}& ={\pi }_{0jk}+{\pi }_{1jk}\left(\text{timepoint}\right)+e_{ijk}\\ {\pi }_{0jk}& ={\beta }_{00k}+{\beta }_{01k}\left(\text{FRL}\right)+r_{0jk}\\ {\pi }_{1jk}& ={\beta }_{10k}\\ & \end{array}$$

In Gelman & Hill

$$\begin{array}{cc}{\mathrm{read}}_i& \sim N({\alpha }_{j\left[i\right]}+{\beta }_1(\mathrm{timepoint}),{\sigma }^2)\\ {\alpha }_j& \sim N({\mu }_{{\alpha }_j},{\sigma }_{{\alpha }_j}^2)\text{, for id j = 1,}\dots \text{,J}\end{array}$$

What does this look like?

Below is a random sample of the model predictions for 20 participants

Parallel slopes

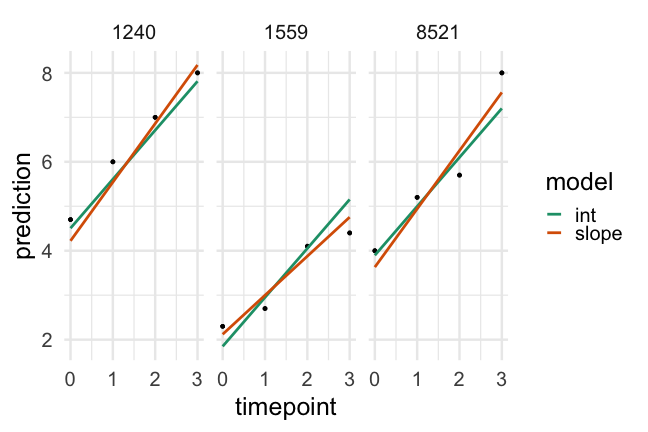
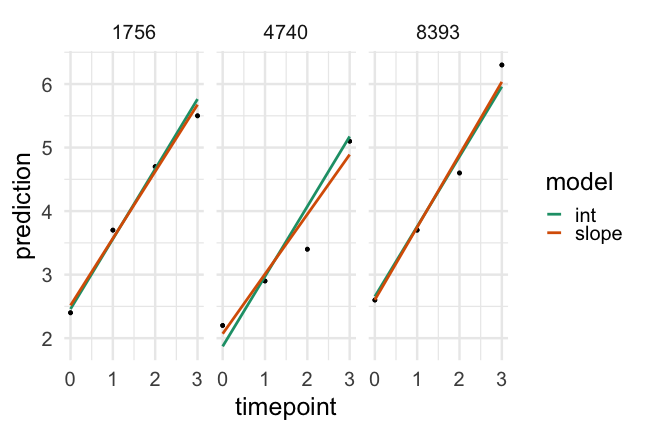
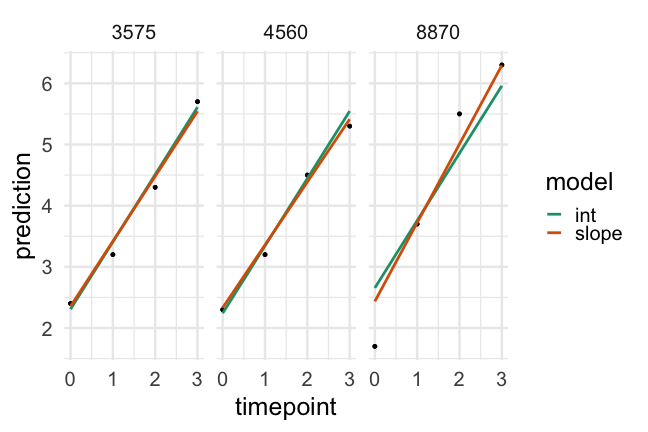
• Had we of fit a standard regression model we would have had one slope to represent the trend of all participants, which would (fairly clearly) be less than ideal

• Now, we've allowed each participant to have a different starting point, but constrained the rate of change to be constant.

• How reasonable is this assumption?

Random sample of 9 participants

And 9 different participants

I would argue this is looking pretty good

Plotting

• I realize I didn't echo the code for the prior plots

• You can look at the source code if you want

• We will talk about making these types of plots next week

Model summary

summary(m_intercepts)Copy Code

## Linear mixed model fit by REML ['lmerMod']
## Formula: read ~ 1 + timepoint + (1 | id)
##    Data: d
## 
## REML criterion at convergence: 3487.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.6170 -0.5207  0.0383  0.5214  3.7428 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  id       (Intercept) 0.7797   0.8830  
##  Residual             0.4609   0.6789  
## Number of obs: 1325, groups:  id, 405
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  2.70374    0.05257   51.43
## timepoint    1.10134    0.01759   62.62
## 
## Correlation of Fixed Effects:
##           (Intr)
## timepoint -0.406Copy Code

Modeling

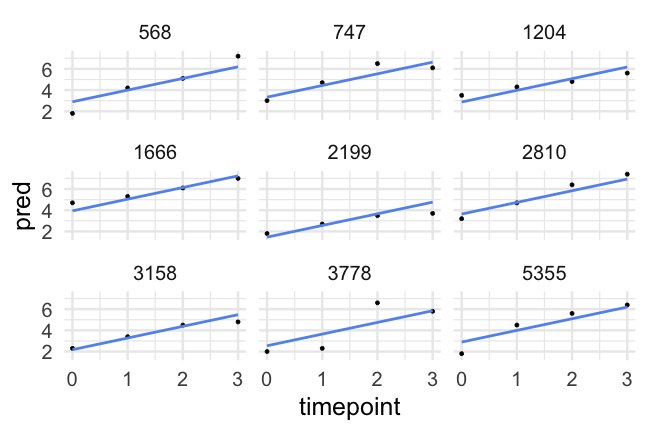
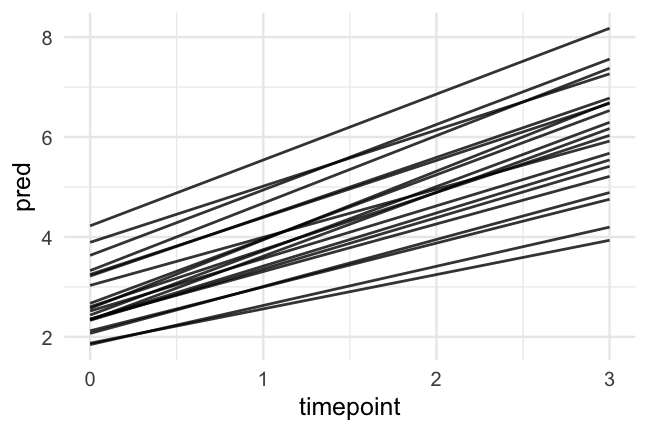
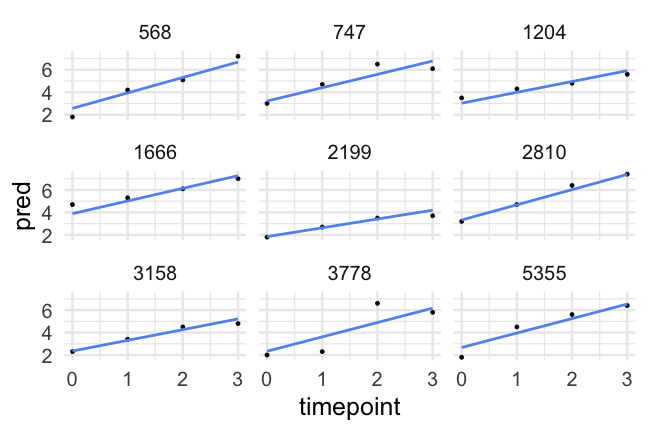
• Let's fit a second model that allows each participant to have a different slope

m_slopes <- lmer(read ~ 1 + timepoint + (1 + timepoint|id),
                     data = d)Copy Code

Quick note on syntax

I'm being very explicit in the above about what I'm estimating. However, intercepts are generally implied. So the above is equivalent to

m_slopes <- lmer(read ~ timepoint + (timepoint|id),
                     data = d)Copy Code

which is actually how I generally write it

Important!

You are not only estimating an additional variance component (variance of the intercept and variance of the slope), but also the covariance among them.

In Gelman & Hill Notation

$$\begin{array}{cc}{\mathrm{read}}_i& \sim N({\alpha }_{j\left[i\right]}+{\beta }_{1j\left[i\right]}(\mathrm{timepoint}),{\sigma }^2)\\ \left(\begin{array}{c}\begin{array}{cc}& {\alpha }_j\\ & {\beta }_{1j}\end{array}\end{array}\right)& \sim N(\left(\begin{array}{c}\begin{array}{cc}& {\mu }_{{\alpha }_j}\\ & {\mu }_{{\beta }_{1j}}\end{array}\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\alpha }_j}^2& {\rho }_{{\alpha }_j{\beta }_{1j}}\\ {\rho }_{{\beta }_{1j}{\alpha }_j}& {\sigma }_{{\beta }_{1j}}^2\end{array}\right))\text{, for id j = 1,}\dots \text{,J}\end{array}$$

Contrast this with R & B

Raudenbush and Bryk

$$\begin{array}{cc}{\text{read}}_{ij}& ={\pi }_{0jk}+{\pi }_{1jk}\left(\text{timepoint}\right)+e_{ijk}\\ {\pi }_{0jk}& ={\beta }_{00k}+{\beta }_{01k}\left(\text{FRL}\right)+r_{0jk}\\ {\pi }_{1jk}& ={\beta }_{10k}+r_{1jk}\\ & \end{array}$$

The covariance estimation is less clear, unless we add the additional distributional assumptions part

$$e_{ijk}\sim N(0,\sigma )$$

$$\begin{array}{cc}\left(\begin{array}{c}\begin{array}{cc}& r_{0jk}\\ & r_{1jk}\end{array}\end{array}\right)& \sim N(\left(\begin{array}{c}\begin{array}{cc}& 0\\ & 0\end{array}\end{array}\right),\left(\begin{array}{cc}{\tau }_{00}& {\tau }_{01}\\ {\tau }_{10}& {\tau }_{11}\end{array}\right))\text{, for id j = 1,}\dots \text{,J}\end{array}$$

Random slopes

Same 20 participants from before. Do they look like they differ?

Look by participant

Same random sample of 9 participants

And an additional 9 different participants

What's the output look like

summary(m_slopes)Copy Code

## Linear mixed model fit by REML ['lmerMod']
## Formula: read ~ 1 + timepoint + (1 + timepoint | id)
##    Data: d
## 
## REML criterion at convergence: 3382
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7161 -0.5201 -0.0220  0.4793  4.1847 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  id       (Intercept) 0.57309  0.7570       
##           timepoint   0.07459  0.2731   0.29
##  Residual             0.34584  0.5881       
## Number of obs: 1325, groups:  id, 405
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  2.69609    0.04530   59.52
## timepoint    1.11915    0.02169   51.60
## 
## Correlation of Fixed Effects:
##           (Intr)
## timepoint -0.155Copy Code

Let's interpret each of the following

• ${\alpha }_{j\left[i\right]}$

• ${\beta }_{1j\left[i\right]}$

• ${\sigma }_{{\alpha }_j}^2$

• ${\rho }_{{\alpha }_j{\beta }_{1j}}$

• ${\sigma }_{{\beta }_{1j}}^2$

In equation form

$$\begin{array}{cc}{\widehat{read}}_i& \sim N({2.7}_{{\alpha }_{j\left[i\right]}}+{1.12}_{{\beta }_{1j\left[i\right]}}(\mathrm{timepoint}),{\sigma }^2)\\ \left(\begin{array}{c}\begin{array}{cc}& {\alpha }_j\\ & {\beta }_{1j}\end{array}\end{array}\right)& \sim N(\left(\begin{array}{c}\begin{array}{cc}& 0\\ & 0\end{array}\end{array}\right),\left(\begin{array}{cc}0.76& 0.29\\ 0.29& 0.27\end{array}\right))\text{, for id j = 1,}\dots \text{,J}\end{array}$$

P values

The {lme4} package does not report $p$-values. This is because its author, Douglas Bates, believes they are fundamentally flawed for multilevel models.

The link above is worth reading through, but basically it is not straightforward to calculate the denominator degrees of freedom for an $F$ test. The methods that are used are approximations and, although generally accepted, are not guaranteed to be correct.

Alternatives

There are two primary work-arounds here:

• Don't use $p$-values, and instead just interpret the confidence intervals, or

• Use the same approximation that others use via {lmerTest} package.

Confidence intervals

Multiple options, but profiled or bootstrap confidence intervals are generally preferred, though computationally intensive. Note that these provide CIs for the variance components as well.

confint(m_slopes)Copy Code

## Computing profile confidence intervals ...Copy Code

##                  2.5 %    97.5 %
## .sig01      0.67961051 0.8365439
## .sig02      0.06898955 0.5434982
## .sig03      0.22282787 0.3213734
## .sigma      0.55548063 0.6238545
## (Intercept) 2.60721096 2.7850364
## timepoint   1.07653165 1.1622218Copy Code

lmerTest

library(lmerTest)
# refit model
m_slopes2 <- lmer(read ~ timepoint + (timepoint|id),
                     data = d)Copy Code

New summary

summary(m_slopes2)Copy Code

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: read ~ timepoint + (timepoint | id)
##    Data: d
## 
## REML criterion at convergence: 3382
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7161 -0.5201 -0.0220  0.4793  4.1847 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  id       (Intercept) 0.57309  0.7570       
##           timepoint   0.07459  0.2731   0.29
##  Residual             0.34584  0.5881       
## Number of obs: 1325, groups:  id, 405
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)   2.69609    0.04530 400.87693   59.52   <2e-16 ***
## timepoint     1.11915    0.02169 308.40833   51.60   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr)
## timepoint -0.155Copy Code

Comparing models

• How do we know which model is preferred?

• We don't want to overfit, but we also don't want to underfit

  • What do these terms mean again?

• Numerous approaches

  • ${\chi }^2$ significance test of the change in the model deviance
  • Information criteria (AIC/BIC)
  • Cross validation procedures

Using built-in approaches

anova(m_intercepts, m_slopes)Copy Code

## refitting model(s) with ML (instead of REML)Copy Code

## Data: d
## Models:
## m_intercepts: read ~ 1 + timepoint + (1 | id)
## m_slopes: read ~ 1 + timepoint + (1 + timepoint | id)
##              npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## m_intercepts    4 3485.1 3505.8 -1738.5   3477.1                         
## m_slopes        6 3383.8 3414.9 -1685.9   3371.8 105.29  2  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Copy Code

What does this mean?

The {performance} package

Similar information, little bit nicer output

library(performance)
compare_performance(m_intercepts, m_slopes) %>% 
  print_md()Copy Code

Table: Comparison of Model Performance Indices

Likelihood ratio test

test_likelihoodratio(m_intercepts, m_slopes) %>% 
  print_md()Copy Code

Or use Bayes factors

This is the default if the models are nested, as ours are

test_performance(m_intercepts, m_slopes) %>% 
  print_md()Copy Code

Models were detected as nested and are compared in sequential order.

Quick note on Bayes factors

• Pure Bayesians typically hate them - they are sometimes called a Bayesain p-value

• Tests under which model the observed data are more likely

• Larger values indicate less support for the comparison model

• I would advise you only use it in combination with other sources of evidence

See here for more information

Final comparison

Let's look at the predictions for a few individual participants

Another 3 participants

One more set

Conclusions

Given the evidence we've looked at I would conclude:

• Both models are a considerable improvement over a linear regression model
• The random intercepts and slopes model is a better fit to the data than the random intercepts only model
• There is more variability in initial starting point than rate of change (which is typical)

• There was a modest correlation between the intercept and the slope, suggesting those who start higher also have steeper rates of change (but this was minor)