Predictions and visualizations

class: center, middle, inverse, title-slide

# Predictions and visualizations
### Daniel Anderson
### Week 3

---

layout: true

---
# Agenda
* Fitting some basic models

* Coefficient plots

* Using the coefficients to make predictions "by hand"
  + contrast with results from `predict()`

* Building predictions for new data

* Marginal effects

---
# Learning objectives
* Understand how to pull different pieces out of the model

* Understand how multilevel models make their predictions for individual observations
  + And specifically how they differ from single-level regression models
  
* Be able to use the output from model objects to visualize different parts of the model.

---
# Read in the data
Let's read in the popularity data so we can fit some really basic models.

You try first

```r
library(tidyverse)
popular <- read_csv(here::here("data", "popularity.csv"))
popular
```

```
## # A tibble: 2,000 x 7
##    pupil class extrav sex    texp popular popteach
##    <dbl> <dbl>  <dbl> <chr> <dbl>   <dbl>    <dbl>
##  1     1     1      5 girl     24     6.3        6
##  2     2     1      7 boy      24     4.9        5
##  3     3     1      4 girl     24     5.3        6
##  4     4     1      3 girl     24     4.7        5
##  5     5     1      5 girl     24     6          6
##  6     6     1      4 boy      24     4.7        5
##  7     7     1      5 boy      24     5.9        5
##  8     8     1      4 boy      24     4.2        5
##  9     9     1      5 boy      24     5.2        5
## 10    10     1      5 boy      24     3.9        3
## # … with 1,990 more rows
```

---
# Fit a basic model

Fit each of the following models

* `popular` as the outcome, with a random intercept for `class`

* `popular` as the outcome, with `sex` included as a fixed effect and a random intercept for `class`

* `popular` as the outcome, with `sex` included as a fixed effect and a random intercept and slope for `class`

---
# Models

```r
library(lme4)
m0 <- lmer(popular ~ 1 + (1|class), popular)
m1 <- lmer(popular ~ sex + (1|class), popular)
m2 <- lmer(popular ~ sex + (sex|class), popular)
```

---
# Compare performance
Use whatever tests you'd like, and come up with the model you think fits the data best

```r
library(performance)
compare_performance(m0, m1, m2) %>% 
  print_md()
```

Table: Comparison of Model Performance Indices

|Name |   Model |     AIC |     BIC | R2 (cond.) | R2 (marg.) |  ICC | RMSE | Sigma |
|:----|:-------:|:-------:|:-------:|:----------:|:----------:|:----:|:----:|:-----:|
|m0   | lmerMod | 6336.51 | 6353.31 |       0.36 |       0.00 | 0.36 | 1.08 |  1.11 |
|m1   | lmerMod | 5572.07 | 5594.48 |       0.53 |       0.26 | 0.37 | 0.89 |  0.91 |
|m2   | lmerMod | 5571.05 | 5604.66 |       0.54 |       0.26 | 0.38 | 0.88 |  0.90 |

---
# Test of the Log-likelihood

```r
test_likelihoodratio(m0, m1) %>% 
  print_md()
```

|Name |  Model | df| df_diff|   Chi2|         p|
|:----|:-------|--:|-------:|------:|---------:|
|m0   |lmerMod |  3|        |       |          |
|m1   |lmerMod |  4|       1| 766.44| 1.07e-168|

```r
test_likelihoodratio(m1, m2) %>% 
  print_md()
```

|Name |  Model | df| df_diff| Chi2|    p|
|:----|:-------|--:|-------:|----:|----:|
|m1   |lmerMod |  4|        |     |     |
|m2   |lmerMod |  6|       2| 5.02| 0.08|

Pretty good evidence that `m1` displays the best fit

---
class: inverse-blue middle

# Coefficient plots

---
# Package options

The [**{parameters}**](https://easystats.github.io/parameters/) package (part of the [**{easystats}**](https://github.com/easystats) ecosystem) will get you where you want to be.

Alternatively, you could use the [**{broom.mixed}**](https://github.com/bbolker/broom.mixed) package (which is a spin-off of the [**{broom}**](https://github.com/tidymodels/broom) package) which requires slightly less code.

I'll illustrate both

```r
install.packages("broom.mixed")
```

---
# {broom.mixed}

```r
library(broom.mixed)
tidy(m0)
```

```
## # A tibble: 3 x 6
##   effect   group    term             estimate   std.error statistic
##   <chr>    <chr>    <chr>               <dbl>       <dbl>     <dbl>
## 1 fixed    <NA>     (Intercept)     5.077860   0.08739443  58.10278
## 2 ran_pars class    sd__(Intercept) 0.8379169 NA           NA      
## 3 ran_pars Residual sd__Observation 1.105348  NA           NA
```

--
Or get just the fixed effects

```r
tidy(m0, effects = "fixed")
```

```
## # A tibble: 1 x 5
##   effect term        estimate  std.error statistic
##   <chr>  <chr>          <dbl>      <dbl>     <dbl>
## 1 fixed  (Intercept) 5.077860 0.08739443  58.10278
```

---
# Across models
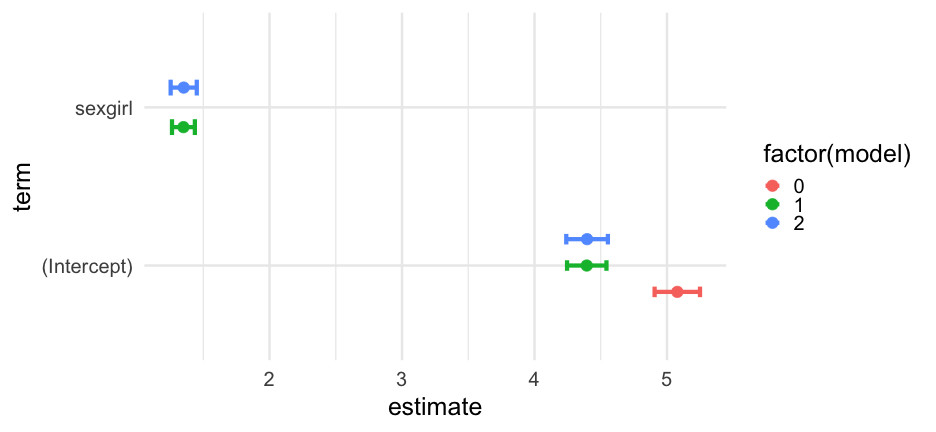
Let's tidy all three models, extracting just the fixed effects, and **adding in a 95% confidence interval**

```r
models <- bind_rows(
  tidy(m0, effects = "fixed", conf.int = TRUE),
  tidy(m1, effects = "fixed", conf.int = TRUE),
  tidy(m2, effects = "fixed", conf.int = TRUE),
  .id = "model"
  ) %>% 
  mutate(model = as.numeric(model) - 1)
models
```

```
## # A tibble: 5 x 8
##   model effect term        estimate  std.error statistic conf.low conf.high
##   <dbl> <chr>  <chr>          <dbl>      <dbl>     <dbl>    <dbl>     <dbl>
## 1     0 fixed  (Intercept) 5.077860 0.08739443  58.10278 4.906570  5.249150
## 2     1 fixed  (Intercept) 4.394460 0.07586494  57.92478 4.245767  4.543152
## 3     1 fixed  sexgirl     1.350102 0.04403301  30.66113 1.263799  1.436405
## 4     2 fixed  (Intercept) 4.396820 0.08012978  54.87123 4.239768  4.553871
## 5     2 fixed  sexgirl     1.352175 0.05029920  26.88263 1.253590  1.450760
```

---
# Plot

```r
pd <- position_dodge(0.5)
ggplot(models, aes(estimate, term, color = factor(model))) +
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high), 
                 position = pd,
                 height = 0.2) +
  geom_point(position = pd)
```

![](w3p1_files/figure-html/unnamed-chunk-10-1.png)

---
# Standardization
The nice thing about tidying the model output, is that the code on the previous slides *will always work* regardless of the model(s) you've fit.

--
## Caveat
I don't actually think the prior plot is all that useful.

* Occasionally helpful to visualize differences between coefficients, but you'll usually want to omit the intercept

* Be careful about scales

* If you were to publish the prior plot, make it prettier and more accessible first

---
# {parameters}

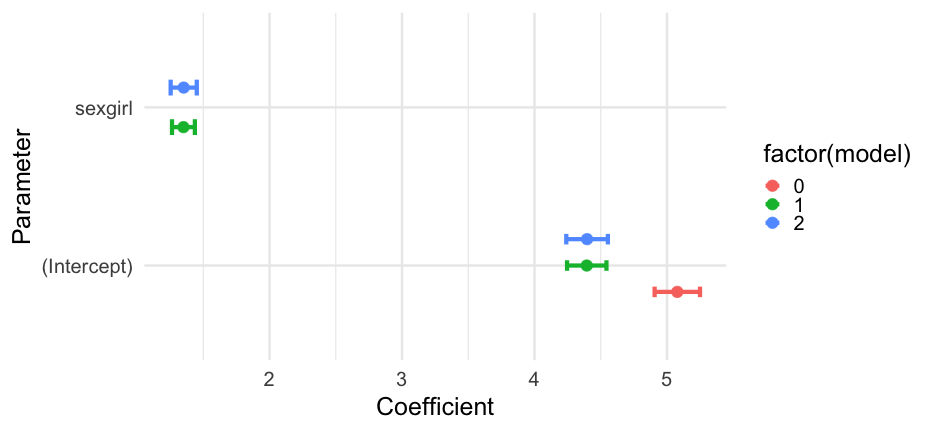
To get basically the same output from parameters:

```r
library(parameters)
parameters(m0) %>% 
  as_tibble()
```

```
## # A tibble: 1 x 10
##   Parameter   Coefficient         SE    CI   CI_low  CI_high        t df_error
##   <chr>             <dbl>      <dbl> <dbl>    <dbl>    <dbl>    <dbl>    <int>
## 1 (Intercept)    5.077860 0.08739443  0.95 4.906570 5.249150 58.10278     1997
## # … with 2 more variables: p <dbl>, Effects <chr>
```

```r
models2 <- bind_rows(
  as_tibble(parameters(m0)),
  as_tibble(parameters(m1)),
  as_tibble(parameters(m2)),
  .id = "model"
  ) %>% 
  mutate(model = as.numeric(model) - 1)
```

---

```r
pd <- position_dodge(0.5)
ggplot(models2, aes(Coefficient, Parameter, 
                    color = factor(model))) +
  geom_errorbarh(aes(xmin = CI_low, xmax = CI_high), 
                 position = pd,
                 height = 0.2) +
  geom_point(position = pd)
```

![](w3p1_files/figure-html/unnamed-chunk-12-1.png)

---
# Other parts of the model
From here on out, I'll just be using **{broom.mixed}** but either package should work, with minor tweaks.

--
## Variance components
Notice that, by default, we don't have any uncertainty

```r
tidy(m0)
```

--
We can fix this by using bootstrap or profiled CIs

---
# Bootstrap CIs

```r
tidy(
  m0,
  effects = "ran_pars", 
  conf.int = TRUE, 
  conf.method = "boot"
)
```

```
## Computing bootstrap confidence intervals ...
```

```
## # A tibble: 2 x 6
##   effect   group    term             estimate  conf.low conf.high
##   <chr>    <chr>    <chr>               <dbl>     <dbl>     <dbl>
## 1 ran_pars class    sd__(Intercept) 0.8379169 0.7145176 0.9652536
## 2 ran_pars Residual sd__Observation 1.105348  1.071117  1.141232
```

---
# m2
Note this takes a bit of time, even though the model is pretty simple. Also these are standard deviations and a correlation, not variances/covariances

```r
tidy(
  m2,
  effects = "ran_pars", 
  conf.int = TRUE, 
  conf.method = "boot"
)
```

```
## Computing bootstrap confidence intervals ...
```

```
## 
## 35 message(s): boundary (singular) fit: see ?isSingular
## 16 warning(s): Model failed to converge with max|grad| = 0.00213278 (tol = 0.002, component 1) (and others)
```

```
## # A tibble: 4 x 6
##   effect   group    term                       estimate    conf.low  conf.high
##   <chr>    <chr>    <chr>                         <dbl>       <dbl>      <dbl>
## 1 ran_pars class    sd__(Intercept)           0.7389520  0.6133643  0.8469480 
## 2 ran_pars class    cor__(Intercept).sexgirl -0.4442543 -1          0.04996563
## 3 ran_pars class    sd__sexgirl               0.2336921  0.04570838 0.3513648 
## 4 ran_pars Residual sd__Observation           0.9049626  0.8744993  0.9341371
```

---
# Quick challenge
Can you make a dotplot with uncertainty for the variance components?

What about a plot showing both fixed effects and variance components?

---
# One approach

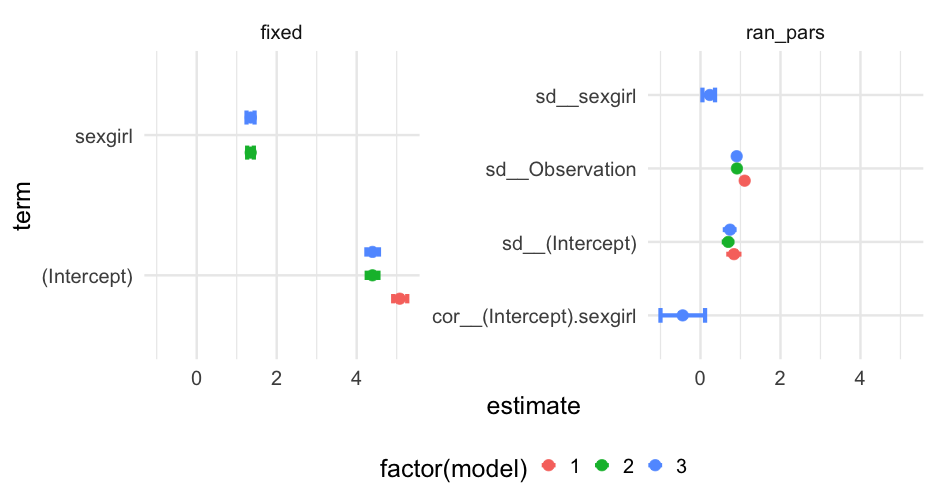
```r
pull_model_results <- function(model) {
  tidy(
    model,
    conf.int = TRUE, 
    conf.method = "boot"
  )
}
full_models <- bind_rows(
  pull_model_results(m0),
  pull_model_results(m1),
  pull_model_results(m2),
  .id = "model"
)
```

```
## Computing bootstrap confidence intervals ...
## Computing bootstrap confidence intervals ...
## Computing bootstrap confidence intervals ...
## Computing bootstrap confidence intervals ...
## Computing bootstrap confidence intervals ...
```

```
## 
## 30 message(s): boundary (singular) fit: see ?isSingular
## 13 warning(s): Model failed to converge with max|grad| = 0.00215039 (tol = 0.002, component 1) (and others)
```

```
## Computing bootstrap confidence intervals ...
```

```
## 
## 30 message(s): boundary (singular) fit: see ?isSingular
## 9 warning(s): Model failed to converge with max|grad| = 0.00203702 (tol = 0.002, component 1) (and others)
```

---

```r
ggplot(full_models, aes(estimate, term, color = factor(model))) +
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high), 
                 position = pd,
                 height = 0.2) +
  geom_point(position = pd) +
  facet_wrap(~effect, scales = "free_y") +
  theme(legend.position = "bottom")
```

![](w3p1_files/figure-html/unnamed-chunk-17-1.png)

---
# Random effects
## Pop Quiz
What's the difference between the output from below and the output on the next slide?

```r
tidy(m0, effects = "ran_vals")
```

```
## # A tibble: 100 x 6
##    effect   group level term            estimate std.error
##    <chr>    <chr> <chr> <chr>              <dbl>     <dbl>
##  1 ran_vals class 1     (Intercept) -0.002630828 0.2370649
##  2 ran_vals class 2     (Intercept) -0.8949875   0.2370649
##  3 ran_vals class 3     (Intercept) -0.3496155   0.2487845
##  4 ran_vals class 4     (Intercept)  0.3318175   0.2222273
##  5 ran_vals class 5     (Intercept)  0.1919485   0.2317938
##  6 ran_vals class 6     (Intercept) -0.6833977   0.2370649
##  7 ran_vals class 7     (Intercept) -0.8062842   0.2317938
##  8 ran_vals class 8     (Intercept) -1.019181    0.2370649
##  9 ran_vals class 9     (Intercept) -0.3844123   0.2370649
## 10 ran_vals class 10    (Intercept)  0.2226622   0.2178678
## # … with 90 more rows
```

---

```r
tidy(m0, effects = "ran_coefs")
```

```
## # A tibble: 100 x 5
##    effect    group level term        estimate
##    <chr>     <chr> <chr> <chr>          <dbl>
##  1 ran_coefs class 1     (Intercept) 5.075229
##  2 ran_coefs class 2     (Intercept) 4.182872
##  3 ran_coefs class 3     (Intercept) 4.728244
##  4 ran_coefs class 4     (Intercept) 5.409677
##  5 ran_coefs class 5     (Intercept) 5.269808
##  6 ran_coefs class 6     (Intercept) 4.394462
##  7 ran_coefs class 7     (Intercept) 4.271575
##  8 ran_coefs class 8     (Intercept) 4.058678
##  9 ran_coefs class 9     (Intercept) 4.693447
## 10 ran_coefs class 10    (Intercept) 5.300522
## # … with 90 more rows
```

---
# Answer
The output from `ran_vals` provides the estimate from `$\alpha_j \sim N(0, \sigma)$`.

The output from `ran_coefs` provides the class-level predictions, i.e., in this case, the intercept + the estimated `ran_vals`.

--
## Example

```r
tidy(m0, effects = "ran_vals")$estimate[1:5] + fixef(m0)[1]
```

```
## [1] 5.075229 4.182872 4.728244 5.409677 5.269808
```

```r
tidy(m0, effects = "ran_coefs")$estimate[1:5]
```

```
## [1] 5.075229 4.182872 4.728244 5.409677 5.269808
```

---
# Let's plot the `ran_vals`

```r
m0_ranvals <- tidy(m0, effects = "ran_vals", conf.int = TRUE)
ggplot(m0_ranvals, aes(level, estimate)) +
  geom_errorbar(aes(ymin = conf.low, ymax = conf.high),
                width = 0.2) +
  geom_point() +
  geom_hline(yintercept = 0, size = 2, color = "magenta")
```

![](w3p1_files/figure-html/unnamed-chunk-21-1.png)

Not super helpful

---
# Try again
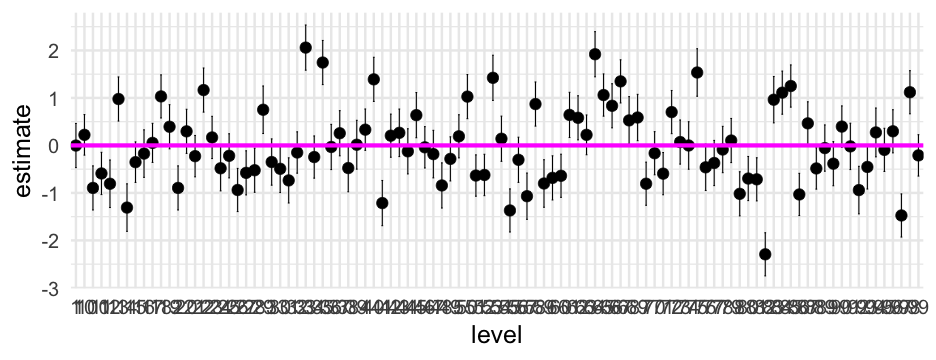
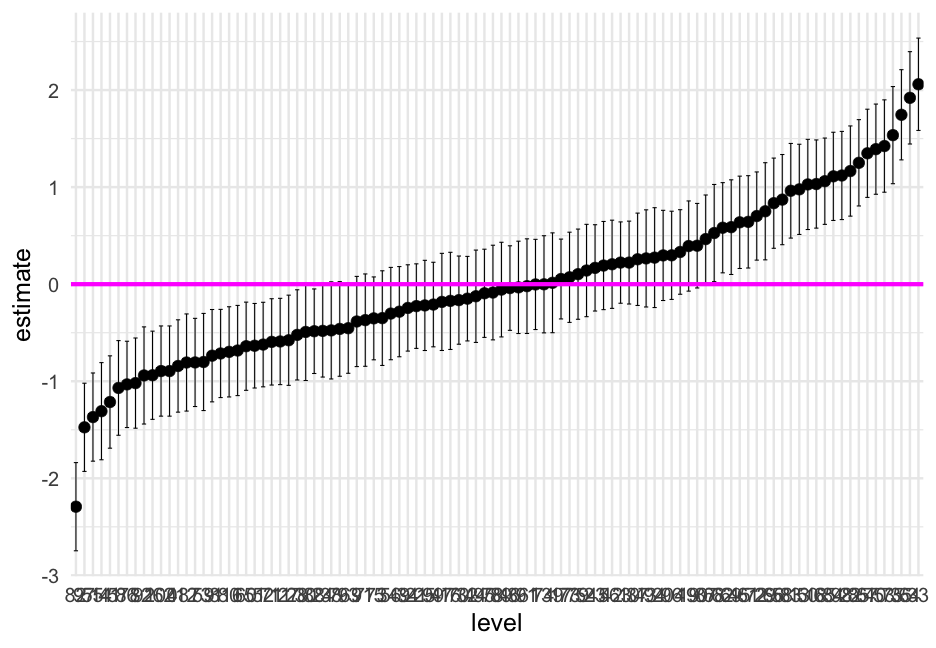
Let's reorder the `level` according to the estimate

```r
m0_ranvals %>% 
* mutate(level = reorder(factor(level), estimate)) %>%
  ggplot(aes(level, estimate)) +
  geom_errorbar(aes(ymin = conf.low, ymax = conf.high),
                width = 0.5) +
  geom_point() +
  geom_hline(yintercept = 0, size = 2, color = "magenta")
```

---
![](w3p1_files/figure-html/unnamed-chunk-23-1.png)

---
# Wrapping up coef plots
* Coefficient plots are generally fairly easy to produce, but often not the most informative

* Random effects plots are probs more informative than the fixed effects/variance components plots

* You can make either a lot more fancy, accessible, etc., and probably should if you're going to use it for publication.

---
class: inverse-green middle
# Break
<div class="countdown" id="timer_60b9027b" style="right:0;bottom:0;" data-warnwhen="0">
<code class="countdown-time"><span class="countdown-digits minutes">05</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code>
</div>

---
class: inverse-red midle
# Making predictions "by hand"

---
# Reminder
Our raw data looks like this

```r
popular
```

---
# Thinking back 
## to standard regression
let's say we fit a model like this

```r
m <- lm(popular ~ 1 + sex, data = popular)
```

--
Our estimated model is

$$
\operatorname{\widehat{popular}} = 4.28 + 1.57(\operatorname{sex}_{\operatorname{girl}})
$$

---
# Making a prediction
What would our model on the prior slide predict for the first student?

```r
pupil1 <- popular[1, ]
pupil1
```

```
## # A tibble: 1 x 7
##   pupil class extrav sex    texp popular popteach
##   <dbl> <dbl>  <dbl> <chr> <dbl>   <dbl>    <dbl>
## 1     1     1      5 girl     24     6.3        6
```

```r
coef(m)[1] + # intercept
  coef(m)[2] * (pupil1$sex == "girl")
```

```
## (Intercept) 
##    5.853314
```

```r
predict(m)[1]
```

```
##        1 
## 5.853314
```

---
# What about this model?
If we use the predict function for `m2`, we get

```r
predict(m2)[1]
```

```
##        1 
## 5.732849
```

### How does the model come up with this prediction?

Use the next few minutes to see if you can write code to replicate it "by hand" as we did with the standard regression model

---
# Thinking through the model
* We have classroom random effects for the intercept and slope

* This means the prediction for an individual is made up of:

+ Overall intercept `+`
  + Overall slope `+`
  + Classroom intercept offset (diff of classroom intercept from overall intercept) `+`
  + Classroom slope offset (diff of classroom slope from overall slope)

---
# Do it!
## First look back at the data

```r
popular[1, ]
```

```
## # A tibble: 1 x 7
##   pupil class extrav sex    texp popular popteach
##   <dbl> <dbl>  <dbl> <chr> <dbl>   <dbl>    <dbl>
## 1     1     1      5 girl     24     6.3        6
```

---
## Next extract the `ran_vals` for the coresponding class

```r
m2_ranvals <- tidy(m2, effects = "ran_vals")
class1_ranvals <- m2_ranvals %>% 
  filter(group == "class" & level == 1)
class1_ranvals
```

```
## # A tibble: 2 x 6
##   effect   group level term           estimate std.error
##   <chr>    <chr> <chr> <chr>             <dbl>     <dbl>
## 1 ran_vals class 1     (Intercept)  0.02657986 0.2240683
## 2 ran_vals class 1     sexgirl     -0.04272575 0.1956483
```

---
# Make prediction

```r
fixef(m2)
```

```
## (Intercept)     sexgirl 
##    4.396820    1.352175
```

```r
fixef(m2)[1] + fixef(m2)[2]*(popular[1, ]$sex == "girl") +
  class1_ranvals$estimate[1] + class1_ranvals$estimate[2]
```

```
## (Intercept) 
##    5.732849
```

--
Confirm

```r
predict(m2)[1]
```

```
##        1 
## 5.732849
```

---
# Challenge
* Without using the `predict()` function, calculate the predicted score for a boy in classroom `10` from `m2`

```r
class10_ranvals <- m2_ranvals %>% 
  filter(group == "class" & level == 10)

fixef(m2)[1] + class10_ranvals$estimate[1]
```

```
## (Intercept) 
##    4.675822
```

---
# Confirm with `predict()`

```r
test <- popular %>% 
  mutate(pred = predict(m2)) %>% 
  filter(class == 10 & sex == "boy") 
test
```

```
## # A tibble: 12 x 8
##    pupil class extrav sex    texp popular popteach     pred
##    <dbl> <dbl>  <dbl> <chr> <dbl>   <dbl>    <dbl>    <dbl>
##  1     1    10      5 boy      21     5.4        5 4.675822
##  2     3    10      5 boy      21     3.4        3 4.675822
##  3     5    10      5 boy      21     5.1        7 4.675822
##  4     7    10      5 boy      21     5.4        4 4.675822
##  5     8    10      5 boy      21     4.9        4 4.675822
##  6    11    10      6 boy      21     4.4        6 4.675822
##  7    12    10      6 boy      21     4.9        5 4.675822
##  8    14    10      6 boy      21     4.8        3 4.675822
##  9    15    10      3 boy      21     3.6        3 4.675822
## 10    16    10      5 boy      21     5          6 4.675822
## 11    17    10      3 boy      21     5.5        5 4.675822
## 12    18    10      6 boy      21     5          4 4.675822
```

---
# More on the predict function

* Once you have the model parameters, you can predict for any values of those parameters

--
Let's fit a slightly more complicated model, using a different longitudinal file than what you used (or are using) in the homework

```r
library(equatiomatic)
head(sim_longitudinal)
```

```
## # A tibble: 6 x 8
## # Groups:   school [1]
##     sid school district group  treatment  prop_low  wave    score
##   <int>  <int>    <int> <chr>  <fct>         <dbl> <dbl>    <dbl>
## 1     1      1        1 medium 1         0.1428571     0 102.2686
## 2     1      1        1 medium 1         0.1428571     1 102.0135
## 3     1      1        1 medium 1         0.1428571     2 102.5216
## 4     1      1        1 medium 1         0.1428571     3 102.2792
## 5     1      1        1 medium 1         0.1428571     4 102.2834
## 6     1      1        1 medium 1         0.1428571     5 102.7963
```

---
# Model
### You try first
* Fit a model with `wave` and `treatment` as predictors of students' `score`. Allow the intercept and the relation between `wave` and `score` to vary by student.

```r
m <- lmer(score ~ wave + treatment + (wave|sid),
          data = sim_longitudinal)
```

---
# Plot predictions
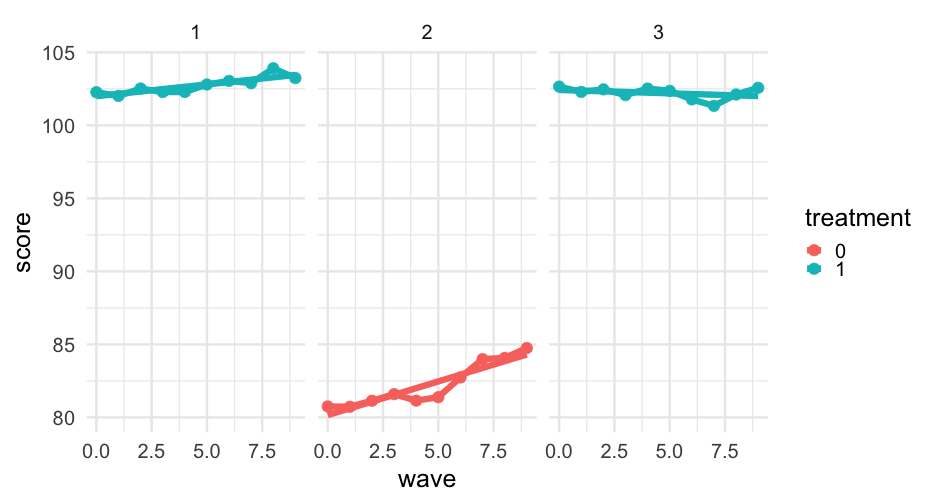
Let's first just limit our data to the first three students.

```r
first_three <- sim_longitudinal %>% 
* ungroup() %>%
  filter(sid %in% 1:3)
```

--
Now try creating a new column in the data with the model predictions for these students. Specify `newdata = first_three` to only make the predictions for those cases.

---

```r
first_three %>% 
  mutate(model_pred = predict(m, newdata = first_three))
```

```
## # A tibble: 30 x 9
##      sid school district group  treatment  prop_low  wave    score model_pred
##    <int>  <int>    <int> <chr>  <fct>         <dbl> <dbl>    <dbl>      <dbl>
##  1     1      1        1 medium 1         0.1428571     0 102.2686   101.9955
##  2     1      1        1 medium 1         0.1428571     1 102.0135   102.1572
##  3     1      1        1 medium 1         0.1428571     2 102.5216   102.3189
##  4     1      1        1 medium 1         0.1428571     3 102.2792   102.4806
##  5     1      1        1 medium 1         0.1428571     4 102.2834   102.6423
##  6     1      1        1 medium 1         0.1428571     5 102.7963   102.8040
##  7     1      1        1 medium 1         0.1428571     6 103.0441   102.9657
##  8     1      1        1 medium 1         0.1428571     7 102.8868   103.1274
##  9     1      1        1 medium 1         0.1428571     8 103.9101   103.2891
## 10     1      1        1 medium 1         0.1428571     9 103.2392   103.4508
## # … with 20 more rows
```

---
# Plot
Try creating a plot with a different `facet` for each `sid` showing the observed trend (relation between `wave` and `score`) as compared to the model prediction. Color the line by whether or not the student was in the treatment group or not.

---

```r
first_three %>% 
  mutate(model_pred = predict(m, newdata = first_three)) %>% 
  ggplot(aes(wave, score, color = treatment)) +
  geom_point() +
  geom_line() +
  geom_line(aes(y = model_pred)) +
  facet_wrap(~sid)
```

![](w3p1_files/figure-html/unnamed-chunk-41-1.png)

---
# Predictions outside our data
Student 2 has a considerably lower intercept. What would we predict the trend would look like if they had been in the treatment group?

--
Try to make this prediction on your own for all time points

---

```r
stu2_trt <- data.frame(
  sid = 2,
  wave = 0:9,
  treatment = factor("1", levels = c(0, 1))
)

predict(m, newdata = stu2_trt)
```

```
##        1        2        3        4        5        6        7        8 
## 78.61702 79.07803 79.53903 80.00004 80.46104 80.92205 81.38305 81.84406 
##        9       10 
## 82.30506 82.76607
```

---
# Compare

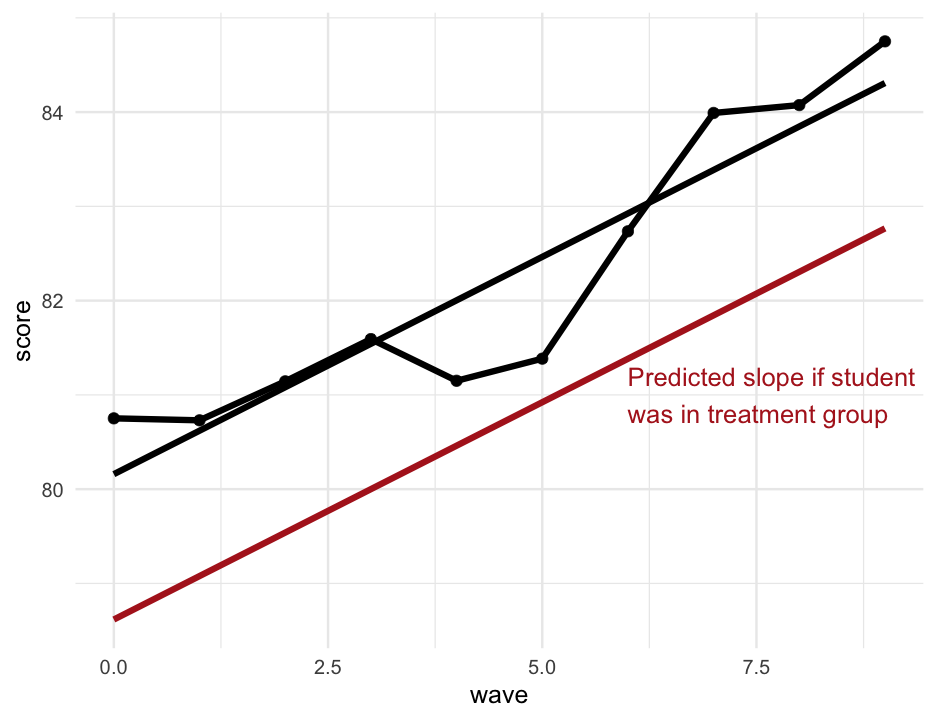
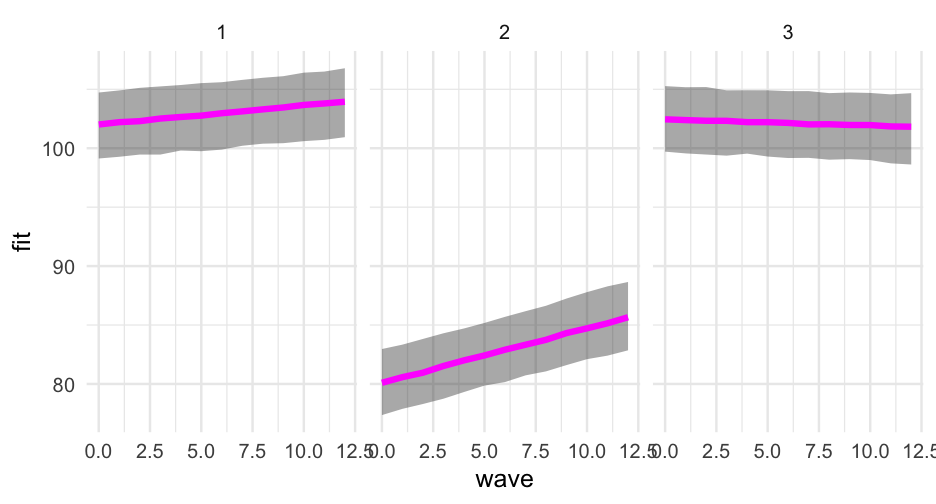
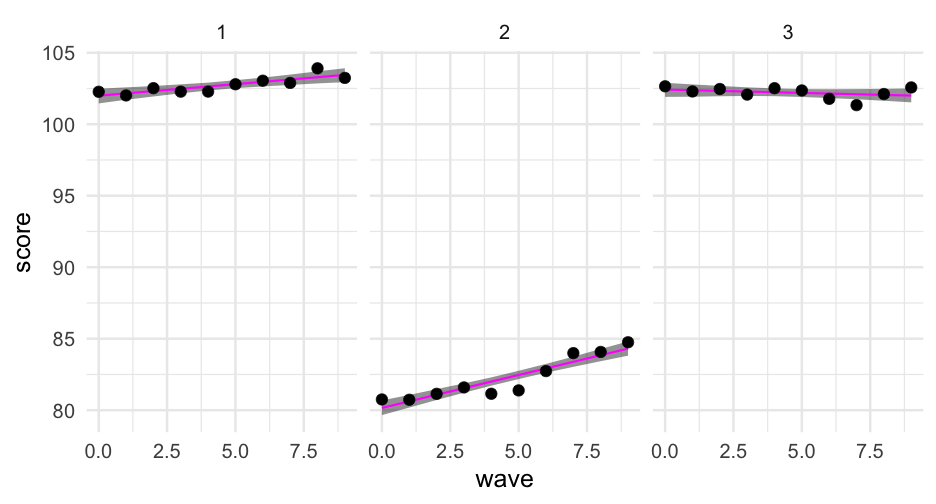
```r
sim_longitudinal %>% 
  filter(sid == 2) %>% 
  mutate(model_pred = predict(m, newdata = .),
         trt_pred = predict(m, newdata = stu2_trt)) %>% 
  ggplot(aes(wave, score)) +
  geom_point() +
  geom_line() +
  geom_line(aes(y = model_pred)) +
  geom_line(aes(y = trt_pred),
            color = "firebrick") +
  annotate(
    "text", 
    x = 6, 
    y = 81, 
    hjust = 0, 
    color = "firebrick", 
    label = "Predicted slope if student\nwas in treatment group"
  )
```

---
![](w3p1_files/figure-html/unnamed-chunk-44-1.png)

---
# Wait... negative?

--
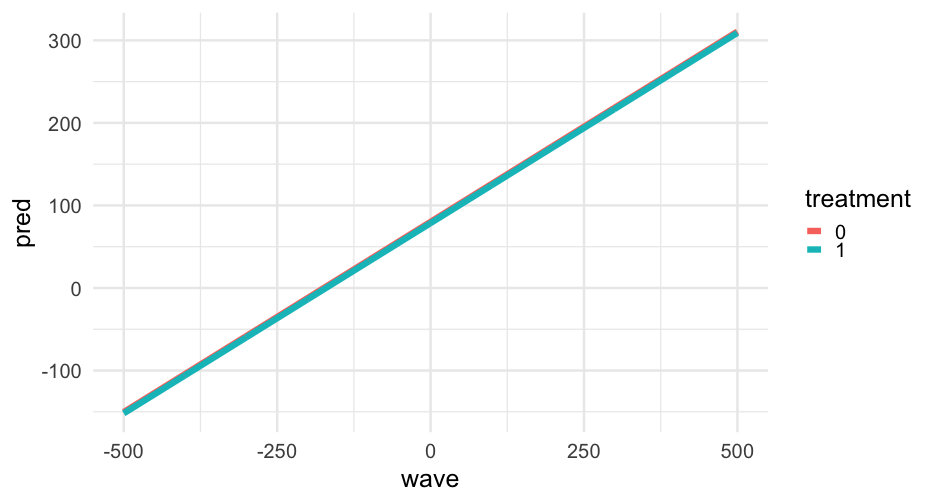
Yes...

```r
arm::display(m)
```

```
## lmer(formula = score ~ wave + treatment + (wave | sid), data = sim_longitudinal)
##             coef.est coef.se
## (Intercept) 97.95     1.38  
## wave         0.17     0.03  
## treatment1  -1.54     1.92  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  sid      (Intercept) 9.74           
##           wave        0.29     -0.16 
##  Residual             0.44           
## ---
## number of obs: 1000, groups: sid, 100
## AIC = 2407.7, DIC = 2393.1
## deviance = 2393.4
```

.gray[Note - I'm just using an alternative function here to get it to fit on the slides easier]

---
# Other projections
We have a *linear* model. This means we can just extend the line to `$\infty$` if we wanted to

--
.realbig[🤪]

```r
newdata_stu2 <- data.frame(
  sid = 2,
  wave = rep(-500:500, 2),
  treatment = factor(rep(c(0, 1), each = length(-500:500)))
)
```

---

```r
newdata_stu2 %>% 
  mutate(pred = predict(m, newdata = newdata_stu2)) %>% 
  ggplot(aes(wave, pred)) +
  geom_line(aes(color = treatment))
```

![](w3p1_files/figure-html/unnamed-chunk-47-1.png)

---
class: inverse-blue middle
# Uncertainty

---
# What to predict?
Let's say we want to predict what time points 10, 11, and 12 would look like for
the first three students.

--
First, create the prediction data frame

```r
pred_frame <- data.frame(
  sid = rep(1:3, each = 13),
  wave = rep(0:12),
  treatment = factor(rep(c(1, 0, 1), each = 13))
)

head(pred_frame)
```

```
##   sid wave treatment
## 1   1    0         1
## 2   1    1         1
## 3   1    2         1
## 4   1    3         1
## 5   1    4         1
## 6   1    5         1
```

---
# merTools
Next, load the [**{merTools}**](https://github.com/jknowles/merTools) package

```r
library(merTools)
```

--
Create a prediction interval with `predictInterval()`, using simulation to obtain the prediction interval

```r
m_pred_interval <- predictInterval(
  m, 
  newdata = pred_frame, 
  level = 0.95
)
```

---

```r
m_pred_interval
```

```
##          fit       upr       lwr
## 1  102.01207 104.72567  99.12815
## 2  102.21023 104.90541  99.27463
## 3  102.29546 105.12290  99.46212
## 4  102.51889 105.24485  99.46114
## 5  102.65108 105.36337  99.80513
## 6  102.76418 105.52242  99.74719
## 7  102.96957 105.60124  99.88279
## 8  103.12596 105.79933 100.20903
## 9  103.29646 105.97636 100.38468
## 10 103.45665 106.11203 100.42733
## 11 103.67235 106.41096 100.59995
## 12 103.79786 106.50498 100.71008
## 13 103.94205 106.78566 100.93741
## 14  80.09841  82.96316  77.35830
## 15  80.57764  83.33608  77.88836
## 16  80.95438  83.81905  78.29942
## 17  81.52330  84.29985  78.74763
## 18  82.00058  84.70749  79.31407
## 19  82.41634  85.17683  79.85975
## 20  82.90433  85.69380  80.15920
## 21  83.32670  86.17170  80.72806
## 22  83.74488  86.63404  81.06728
## 23  84.31655  87.24745  81.60025
## 24  84.71815  87.79115  82.10399
## 25  85.14727  88.28133  82.40308
## 26  85.65959  88.65188  82.85234
## 27 102.45376 105.27047  99.71076
## 28 102.38756 105.17645  99.56086
## 29 102.32892 105.19029  99.46407
## 30 102.32501 104.91057  99.37041
## 31 102.21161 104.91994  99.54185
## 32 102.20953 104.91597  99.29393
## 33 102.14807 104.84285  99.16836
## 34 102.02224 104.84638  99.18406
## 35 102.03473 104.67471  99.02696
## 36 101.97196 104.73033  99.07564
## 37 101.96588 104.69053  98.99436
## 38 101.84893 104.56803  98.71735
## 39 101.82603 104.67284  98.61854
```

---
# Binding data together
Let's add these predictions back to our prediction data frame, then plot them

```r
bind_cols(pred_frame, m_pred_interval)
```

```
##    sid wave treatment       fit       upr       lwr
## 1    1    0         1 102.01207 104.72567  99.12815
## 2    1    1         1 102.21023 104.90541  99.27463
## 3    1    2         1 102.29546 105.12290  99.46212
## 4    1    3         1 102.51889 105.24485  99.46114
## 5    1    4         1 102.65108 105.36337  99.80513
## 6    1    5         1 102.76418 105.52242  99.74719
## 7    1    6         1 102.96957 105.60124  99.88279
## 8    1    7         1 103.12596 105.79933 100.20903
## 9    1    8         1 103.29646 105.97636 100.38468
## 10   1    9         1 103.45665 106.11203 100.42733
## 11   1   10         1 103.67235 106.41096 100.59995
## 12   1   11         1 103.79786 106.50498 100.71008
## 13   1   12         1 103.94205 106.78566 100.93741
## 14   2    0         0  80.09841  82.96316  77.35830
## 15   2    1         0  80.57764  83.33608  77.88836
## 16   2    2         0  80.95438  83.81905  78.29942
## 17   2    3         0  81.52330  84.29985  78.74763
## 18   2    4         0  82.00058  84.70749  79.31407
## 19   2    5         0  82.41634  85.17683  79.85975
## 20   2    6         0  82.90433  85.69380  80.15920
## 21   2    7         0  83.32670  86.17170  80.72806
## 22   2    8         0  83.74488  86.63404  81.06728
## 23   2    9         0  84.31655  87.24745  81.60025
## 24   2   10         0  84.71815  87.79115  82.10399
## 25   2   11         0  85.14727  88.28133  82.40308
## 26   2   12         0  85.65959  88.65188  82.85234
## 27   3    0         1 102.45376 105.27047  99.71076
## 28   3    1         1 102.38756 105.17645  99.56086
## 29   3    2         1 102.32892 105.19029  99.46407
## 30   3    3         1 102.32501 104.91057  99.37041
## 31   3    4         1 102.21161 104.91994  99.54185
## 32   3    5         1 102.20953 104.91597  99.29393
## 33   3    6         1 102.14807 104.84285  99.16836
## 34   3    7         1 102.02224 104.84638  99.18406
## 35   3    8         1 102.03473 104.67471  99.02696
## 36   3    9         1 101.97196 104.73033  99.07564
## 37   3   10         1 101.96588 104.69053  98.99436
## 38   3   11         1 101.84893 104.56803  98.71735
## 39   3   12         1 101.82603 104.67284  98.61854
```

---
# Plot

```r
bind_cols(pred_frame, m_pred_interval) %>% 
  ggplot(aes(wave, fit)) +
  geom_ribbon(aes(ymin = lwr, ymax = upr),
              alpha = 0.4) +
  geom_line(color = "magenta") +
  facet_wrap(~sid)
```

![](w3p1_files/figure-html/unnamed-chunk-53-1.png)

---
# How?
What's really going on here?

See [here](https://cran.rstudio.com/web/packages/merTools/vignettes/Using_predictInterval.html) for a full description, but basically:

1. Creates a simulated (with `n.sim` samples) distribution for each model parameter
2. Computes a distribution of predictions
3. Returns the specifics of the prediction distribution, as requested (e.g., `fit` is the mean or median, and `upr` and `lwr` are the corresponding quaniteles for the uncertainty range)

---
# Disclaimer
According to the **{lme4}** authors

> There is no option for computing standard errors of predictions because it is difficult to define an efficient method that incorporates uncertainty in the variance parameters; we recommend lme4::bootMer() for this task.

--
The `predictInterval()` function is an approximation, while `bootMer()` is the "gold standard" (it just takes a long time)

---
# Boostrapping

Write a function to compute the predictions for each bootstrap resample

```r
pred_fun <- function(fit) {
  predict(fit, newdata = pred_frame)
}
```

Notice we're using the same prediction data frame

---
# Now create BS Estimates

Note this takes a few seconds, and for bigger models may take a *long* time

```r
b <- bootMer(
  m, 
  nsim = 1000, 
  FUN = pred_fun,
  use.u = TRUE, 
  seed = 42
)
```

--
The predictions are stored in a matrix `t`

```r
dim(b$t)
```

```
## [1] 1000   39
```

Each row of the matrix is the prediction for the given bootstrap estimate

---
# Lots of options
There are lots of things you could do with this now.  I'll move it to a data frame first

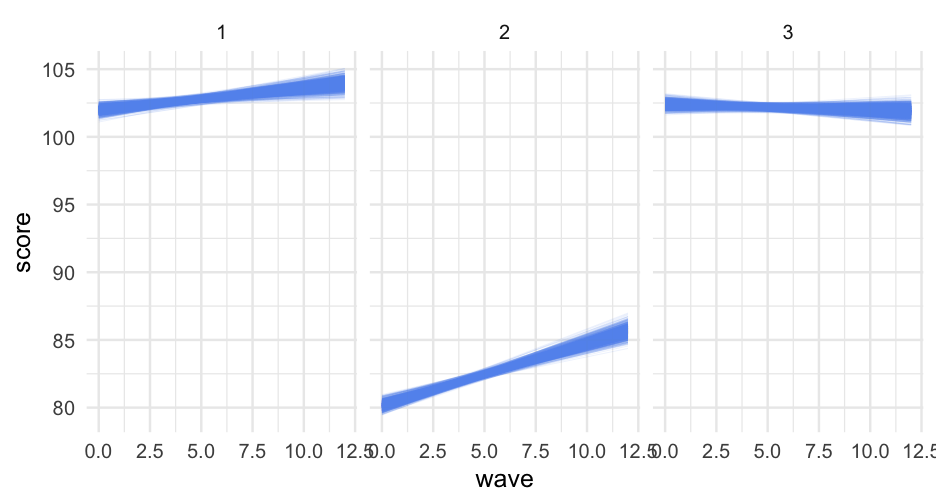
```r
bd <- as.data.frame(t(b$t)) %>% 
  mutate(sid = rep(1:3, each = 13),
         wave = rep(0:12, 3)) %>% 
  pivot_longer(
    starts_with("V"),
    names_to = "bootstrap_sample",
    names_prefix = "V",
    names_transform = list(bootstrap_sample = as.numeric),
    values_to = "score"
  ) %>% 
  arrange(sid, bootstrap_sample, wave)
```

---

```r
bd
```

```
## # A tibble: 39,000 x 4
##      sid  wave bootstrap_sample    score
##    <int> <int>            <dbl>    <dbl>
##  1     1     0                1 102.1749
##  2     1     1                1 102.3497
##  3     1     2                1 102.5245
##  4     1     3                1 102.6992
##  5     1     4                1 102.8740
##  6     1     5                1 103.0488
##  7     1     6                1 103.2235
##  8     1     7                1 103.3983
##  9     1     8                1 103.5731
## 10     1     9                1 103.7478
## # … with 38,990 more rows
```

---
# Plot

```r
ggplot(bd, aes(wave, score)) +
  geom_line(aes(group = bootstrap_sample),
            size = 0.1,
            alpha = 0.5,
            color = "cornflowerblue") +
  facet_wrap(~sid)
```

![](w3p1_files/figure-html/unnamed-chunk-58-1.png)

---
# Prefer ribbons?

```r
bd_ribbons <- bd %>% 
  group_by(sid, wave) %>% 
  summarize(quantile = quantile(score, c(0.025, 0.975)),
            group = c("lower", "upper")) %>% 
  pivot_wider(names_from = "group", values_from = "quantile")
bd_ribbons
```

```
## # A tibble: 39 x 4
## # Groups:   sid, wave [39]
##      sid  wave    lower    upper
##    <int> <int>    <dbl>    <dbl>
##  1     1     0 101.4553 102.4854
##  2     1     1 101.7114 102.5782
##  3     1     2 101.9408 102.6748
##  4     1     3 102.1633 102.7898
##  5     1     4 102.3576 102.9110
##  6     1     5 102.5236 103.0809
##  7     1     6 102.6428 103.2611
##  8     1     7 102.7468 103.4728
##  9     1     8 102.8555 103.6996
## 10     1     9 102.9428 103.9153
## # … with 29 more rows
```

---
# Join with real data

```r
bd_ribbons <- left_join(first_three, bd_ribbons) %>% 
  mutate(pred = predict(m, newdata = first_three))
```

```
## Joining, by = c("sid", "wave")
```

---
# Plot again

```r
ggplot(bd_ribbons, aes(wave, score)) +
  geom_ribbon(aes(ymin = lower, ymax = upper),
              alpha = 0.5) +
  geom_line(aes(y = pred), size = 1, color = "magenta") +
  geom_point() +
  facet_wrap(~sid)
```

![](w3p1_files/figure-html/unnamed-chunk-61-1.png)

---
# Important
There are different types of bootstrap resampling you can choose from

* Do you want to randomly sample from the random effects also? `use.u = FALSE`

* Do you want to assume the random effect estimates are true, and just sample the rest? `use.u = TRUE`

--
Honestly - this is a bit confusing to me, and the results from `use.u = FALSE` didn't make much sense to me. But see [here](https://github.com/lme4/lme4/issues/388) and [here](https://stats.stackexchange.com/questions/147836/prediction-interval-for-lmer-mixed-effects-model-in-r) for more information

---
class: inverse-blue middle
# More complications

---
# Interactions

Let's create an interaction between `treatment` and `wave`

--
### Conceptually: what would this mean?

--
Let's also add in a school-level random effect for the intercept

---
# Interactions
Specified just like with `lm()`. Each of the below are equivalent

```r
wave + treatment + wave:treatment
```

```r
wave * treatment
```

where the latter just expands out to the former.

---
# Adding additional levels
There are a few ways to do this:
* Assume your IDs are all unique
  + implicit nesting
* Don't worry and the IDs, and specify the nesting through the formula
  + Will result in equivalent estimates if the IDs are unique

See [here](https://www.muscardinus.be/2017/07/lme4-random-effects/) for more examples

---
# Implicit nesting

```r
m1a <- lmer(score ~ wave*treatment + 
              (wave|sid) + (1|school),
            data = sim_longitudinal)
arm::display(m1a)
```

```
## lmer(formula = score ~ wave * treatment + (wave | sid) + (1 | 
##     school), data = sim_longitudinal)
##                 coef.est coef.se
## (Intercept)     96.80     1.57  
## wave             0.40     0.03  
## treatment1       0.61     1.88  
## wave:treatment1 -0.45     0.04  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  sid      (Intercept) 9.16           
##           wave        0.19     -0.13 
##  school   (Intercept) 3.27           
##  Residual             0.44           
## ---
## number of obs: 1000, groups: sid, 100; school, 15
## AIC = 2330, DIC = 2301.2
## deviance = 2306.6
```

---
# Explicit nesting

```r
m1b <- lmer(score ~ wave*treatment + 
              (wave|sid:school) + (1|school) ,
            data = sim_longitudinal)
arm::display(m1b)
```

```
## lmer(formula = score ~ wave * treatment + (wave | sid:school) + 
##     (1 | school), data = sim_longitudinal)
##                 coef.est coef.se
## (Intercept)     96.80     1.57  
## wave             0.40     0.03  
## treatment1       0.61     1.88  
## wave:treatment1 -0.45     0.04  
## 
## Error terms:
##  Groups     Name        Std.Dev. Corr  
##  sid:school (Intercept) 9.16           
##             wave        0.19     -0.13 
##  school     (Intercept) 3.27           
##  Residual               0.44           
## ---
## number of obs: 1000, groups: sid:school, 100; school, 15
## AIC = 2330, DIC = 2301.2
## deviance = 2306.6
```

---
# Predictions "by hand"
This is now a three-level model. How does it differ from two-level models in terms of model predictions?

--
Let's make a prediction for the first student at the fourth time point:

```r
sim_longitudinal[4, ]
```

```
## # A tibble: 1 x 8
## # Groups:   school [1]
##     sid school district group  treatment  prop_low  wave    score
##   <int>  <int>    <int> <chr>  <fct>         <dbl> <dbl>    <dbl>
## 1     1      1        1 medium 1         0.1428571     3 102.2792
```

---
# The pieces

```r
fixed <- fixef(m1a)
ranefs <- ranef(m1a)
fixed
```

```
##     (Intercept)            wave      treatment1 wave:treatment1 
##      96.7973387       0.4010222       0.6080336      -0.4459053
```

```r
# Pull just the ranefs for sid 1 and school 1
sid_ranefs <- ranefs$sid[1, ] 
sid_ranefs
```

```
##   (Intercept)      wave
## 1     1.85279 0.1936603
```

```r
sch_ranefs <- ranefs$school[1, ]
sch_ranefs
```

```
## [1] 2.795928
```

---
# Putting it together

```r
(fixed[1] + sid_ranefs[1] + sch_ranefs) + # intercept
  
((fixed[2] + sid_ranefs[2]) * 3) + # fourth timepoint
  
(fixed[3] * 1) + # treatment effect

(fixed[4] * 3)  # treatment by wave effect
```

```
##   (Intercept)
## 1    102.5004
```

---
# Confirm

```r
predict(m1a, newdata = sim_longitudinal[4, ])
```

```
##        1 
## 102.5004
```

---
# Predictions 
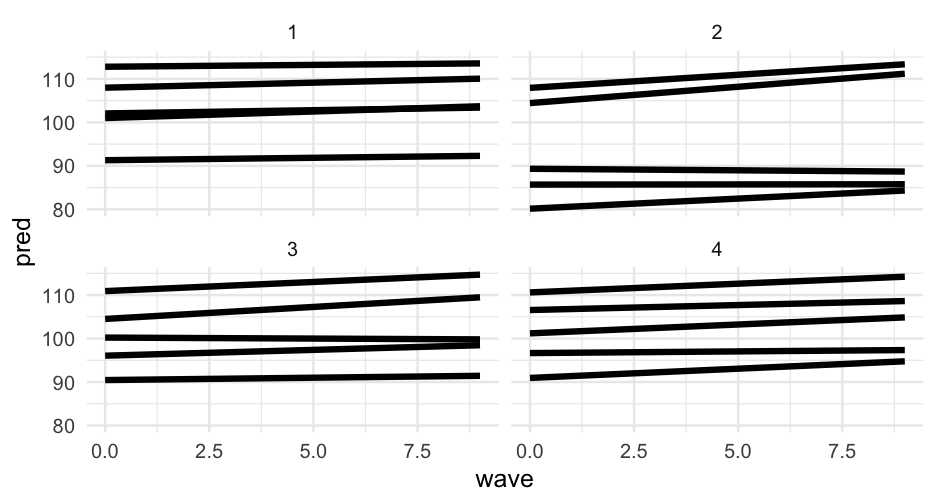
Let's randomly sample 5 students in the first four school and display the model predictions for those students.

There are many ways to create the sample, here's one:

```r
samp <- sim_longitudinal %>% 
  filter(school %in% 1:4) %>% 
  group_by(school, sid) %>% 
  nest()
samp
```

```
## # A tibble: 28 x 3
## # Groups:   sid, school [28]
##      sid school data             
##    <int>  <int> <list>           
##  1     1      1 <tibble [10 × 6]>
##  2    33      3 <tibble [10 × 6]>
##  3    34      4 <tibble [10 × 6]>
##  4    46      1 <tibble [10 × 6]>
##  5    61      1 <tibble [10 × 6]>
##  6    77      2 <tibble [10 × 6]>
##  7    78      3 <tibble [10 × 6]>
##  8    91      1 <tibble [10 × 6]>
##  9    93      3 <tibble [10 × 6]>
## 10     2      2 <tibble [10 × 6]>
## # … with 18 more rows
```

---
# Select 5 rows for each school

```r
set.seed(42)
samp %>% 
  group_by(school) %>% 
  sample_n(5)
```

```
## # A tibble: 20 x 3
## # Groups:   school [4]
##      sid school data             
##    <int>  <int> <list>           
##  1     1      1 <tibble [10 × 6]>
##  2    76      1 <tibble [10 × 6]>
##  3    31      1 <tibble [10 × 6]>
##  4    16      1 <tibble [10 × 6]>
##  5    46      1 <tibble [10 × 6]>
##  6    62      2 <tibble [10 × 6]>
##  7     2      2 <tibble [10 × 6]>
##  8    92      2 <tibble [10 × 6]>
##  9    77      2 <tibble [10 × 6]>
## 10    47      2 <tibble [10 × 6]>
## 11    63      3 <tibble [10 × 6]>
## 12    18      3 <tibble [10 × 6]>
## 13    33      3 <tibble [10 × 6]>
## 14    48      3 <tibble [10 × 6]>
## 15    78      3 <tibble [10 × 6]>
## 16    19      4 <tibble [10 × 6]>
## 17    49      4 <tibble [10 × 6]>
## 18     4      4 <tibble [10 × 6]>
## 19    79      4 <tibble [10 × 6]>
## 20    94      4 <tibble [10 × 6]>
```

---
# `unnest()`

```r
set.seed(42)
samp <- samp %>% 
  group_by(school) %>% 
  sample_n(5) %>% 
  unnest(data) %>% 
  ungroup()
samp
```

```
## # A tibble: 200 x 8
##      sid school district group  treatment  prop_low  wave    score
##    <int>  <int>    <int> <chr>  <fct>         <dbl> <dbl>    <dbl>
##  1     1      1        1 medium 1         0.1428571     0 102.2686
##  2     1      1        1 medium 1         0.1428571     1 102.0135
##  3     1      1        1 medium 1         0.1428571     2 102.5216
##  4     1      1        1 medium 1         0.1428571     3 102.2792
##  5     1      1        1 medium 1         0.1428571     4 102.2834
##  6     1      1        1 medium 1         0.1428571     5 102.7963
##  7     1      1        1 medium 1         0.1428571     6 103.0441
##  8     1      1        1 medium 1         0.1428571     7 102.8868
##  9     1      1        1 medium 1         0.1428571     8 103.9101
## 10     1      1        1 medium 1         0.1428571     9 103.2392
## # … with 190 more rows
```

---
# Make prediction

```r
samp %>% 
  mutate(pred = predict(m1a, newdata = samp))
```

```
## # A tibble: 200 x 9
##      sid school district group  treatment  prop_low  wave    score     pred
##    <int>  <int>    <int> <chr>  <fct>         <dbl> <dbl>    <dbl>    <dbl>
##  1     1      1        1 medium 1         0.1428571     0 102.2686 102.0541
##  2     1      1        1 medium 1         0.1428571     1 102.0135 102.2029
##  3     1      1        1 medium 1         0.1428571     2 102.5216 102.3516
##  4     1      1        1 medium 1         0.1428571     3 102.2792 102.5004
##  5     1      1        1 medium 1         0.1428571     4 102.2834 102.6492
##  6     1      1        1 medium 1         0.1428571     5 102.7963 102.7980
##  7     1      1        1 medium 1         0.1428571     6 103.0441 102.9468
##  8     1      1        1 medium 1         0.1428571     7 102.8868 103.0955
##  9     1      1        1 medium 1         0.1428571     8 103.9101 103.2443
## 10     1      1        1 medium 1         0.1428571     9 103.2392 103.3931
## # … with 190 more rows
```

---
# Plot

```r
samp %>% 
  mutate(pred = predict(m1a, newdata = samp)) %>% 
  ggplot(aes(wave, pred, group = sid)) +
  geom_line() +
  facet_wrap(~school)
```

![](w3p1_files/figure-html/unnamed-chunk-74-1.png)

---
class: inverse-blue middle
# Marginal effects

---
# Marginal effect
A marginal effect shows the relation between one variable in the model and the outcome, while averaging over the other predictors in the model

--
Let's start by making the models slightly more complicated

```r
m2 <- lmer(score ~ wave*treatment + group + prop_low +
              (wave|sid) + (1|school) ,
            data = sim_longitudinal)
```

---

```r
arm::display(m2, detail = TRUE)
```

```
## lmer(formula = score ~ wave * treatment + group + prop_low + 
##     (wave | sid) + (1 | school), data = sim_longitudinal)
##                 coef.est coef.se t value
## (Intercept)      97.62     4.70   20.78 
## wave              0.40     0.03   14.38 
## treatment1        0.82     1.91    0.43 
## grouplow         -4.83     4.00   -1.21 
## groupmedium      -3.61     3.75   -0.96 
## prop_low          9.34    10.21    0.91 
## wave:treatment1  -0.45     0.04  -11.42 
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  sid      (Intercept) 9.18           
##           wave        0.19     -0.13 
##  school   (Intercept) 3.41           
##  Residual             0.44           
## ---
## number of obs: 1000, groups: sid, 100; school, 15
## AIC = 2319.8, DIC = 2313.2
## deviance = 2304.5
```

---
# Marginal effect
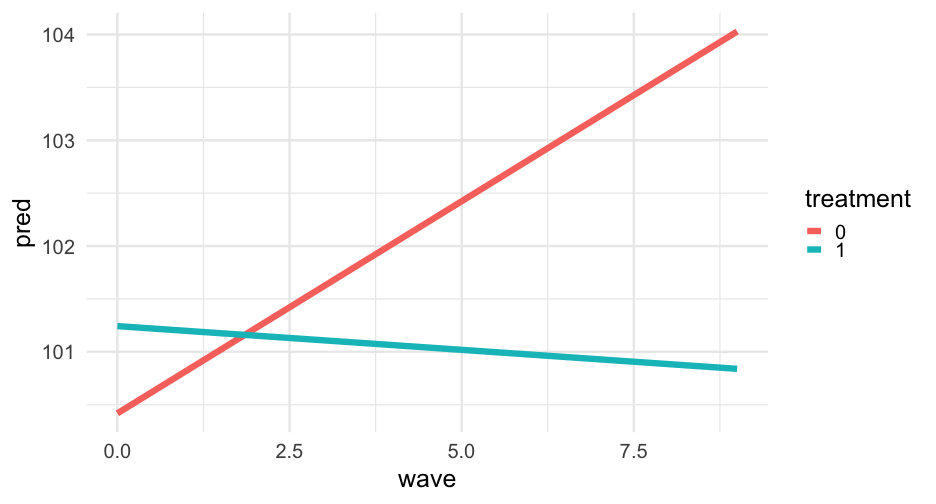
Let's look at the relation between `wave` and `score` by `treatment`, holding the other values constant.

--
First, build a prediction data frame. We'll make population-level prediction - i.e., ignoring the random effects.

```r
marginal_frame1 <- data.frame(
  wave = rep(0:9, 2),
  treatment = as.factor(rep(c(0, 1), each = 10)),
  group = factor("high", levels = c("low", "medium", "high")),
  prop_low = mean(sim_longitudinal$prop_low, na.rm = TRUE),
  sid = -999,
  school = -999
)
```

--
The length of each of these variables can sometimes get a little tricky

---

```r
marginal_frame1
```

```
##    wave treatment group prop_low  sid school
## 1     0         0  high      0.3 -999   -999
## 2     1         0  high      0.3 -999   -999
## 3     2         0  high      0.3 -999   -999
## 4     3         0  high      0.3 -999   -999
## 5     4         0  high      0.3 -999   -999
## 6     5         0  high      0.3 -999   -999
## 7     6         0  high      0.3 -999   -999
## 8     7         0  high      0.3 -999   -999
## 9     8         0  high      0.3 -999   -999
## 10    9         0  high      0.3 -999   -999
## 11    0         1  high      0.3 -999   -999
## 12    1         1  high      0.3 -999   -999
## 13    2         1  high      0.3 -999   -999
## 14    3         1  high      0.3 -999   -999
## 15    4         1  high      0.3 -999   -999
## 16    5         1  high      0.3 -999   -999
## 17    6         1  high      0.3 -999   -999
## 18    7         1  high      0.3 -999   -999
## 19    8         1  high      0.3 -999   -999
## 20    9         1  high      0.3 -999   -999
```

---
# Make predictions!
Note that we have to specify to allow new levels

```r
marginal_frame1 <- marginal_frame1 %>% 
  mutate(pred = predict(m2, 
                        newdata = marginal_frame1, 
                        allow.new.levels = TRUE))
marginal_frame1
```

```
##    wave treatment group prop_low  sid school     pred
## 1     0         0  high      0.3 -999   -999 100.4186
## 2     1         0  high      0.3 -999   -999 100.8196
## 3     2         0  high      0.3 -999   -999 101.2207
## 4     3         0  high      0.3 -999   -999 101.6217
## 5     4         0  high      0.3 -999   -999 102.0227
## 6     5         0  high      0.3 -999   -999 102.4237
## 7     6         0  high      0.3 -999   -999 102.8248
## 8     7         0  high      0.3 -999   -999 103.2258
## 9     8         0  high      0.3 -999   -999 103.6268
## 10    9         0  high      0.3 -999   -999 104.0278
## 11    0         1  high      0.3 -999   -999 101.2433
## 12    1         1  high      0.3 -999   -999 101.1984
## 13    2         1  high      0.3 -999   -999 101.1536
## 14    3         1  high      0.3 -999   -999 101.1087
## 15    4         1  high      0.3 -999   -999 101.0638
## 16    5         1  high      0.3 -999   -999 101.0189
## 17    6         1  high      0.3 -999   -999 100.9740
## 18    7         1  high      0.3 -999   -999 100.9291
## 19    8         1  high      0.3 -999   -999 100.8843
## 20    9         1  high      0.3 -999   -999 100.8394
```

---
# Plot it

```r
ggplot(marginal_frame1, aes(wave, pred, color = treatment)) +
  geom_line()
```

![](w3p1_files/figure-html/unnamed-chunk-80-1.png)

---
# Why do this?
As the model gets more complicated, it can be increasingly difficult to understand the fixed effects.

Plotting the marginal effects regularly helps (e.g., for interactions and non-linear terms)

---
# Try again
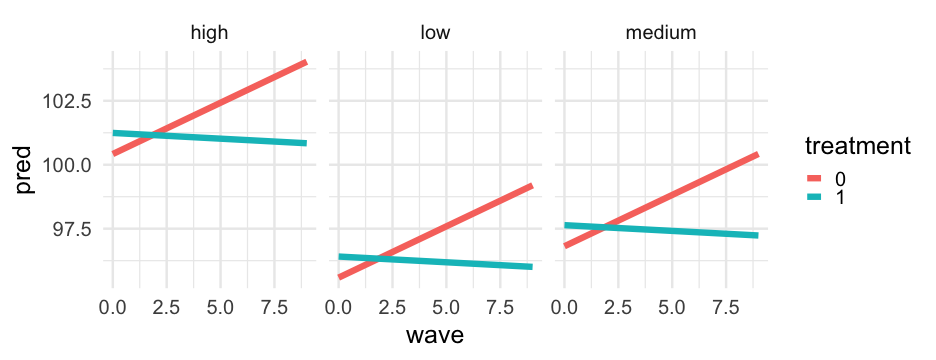
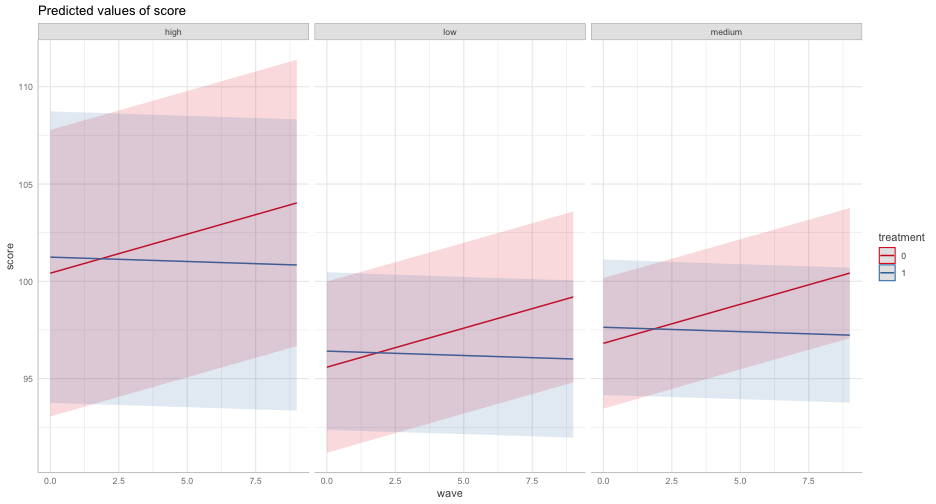
This time, let's look at the same thing, but for all groups, still holding `prop_low` constant.

```r
marginal_frame2 <- data.frame(
  wave = rep(0:9, 2*3),
  treatment = as.factor(rep(c(0, 1), each = 10*3)),
  group = factor(
    rep(
      rep(c("low", "medium", "high"), each = 10),
      2
    )
  ),
  prop_low = mean(sim_longitudinal$prop_low, na.rm = TRUE),
  sid = -999,
  school = -999
)
```

---
# Predict & plot

```r
marginal_frame2 %>% 
  mutate(
    pred = predict(m2, 
                   newdata = marginal_frame2, 
                   allow.new.levels = TRUE)
  ) %>% 
  ggplot(aes(wave, pred, color = treatment)) +
  geom_line() +
  facet_wrap(~group)
```

![](w3p1_files/figure-html/unnamed-chunk-82-1.png)

---
# Automated method
We can build this up on our own with new data frames

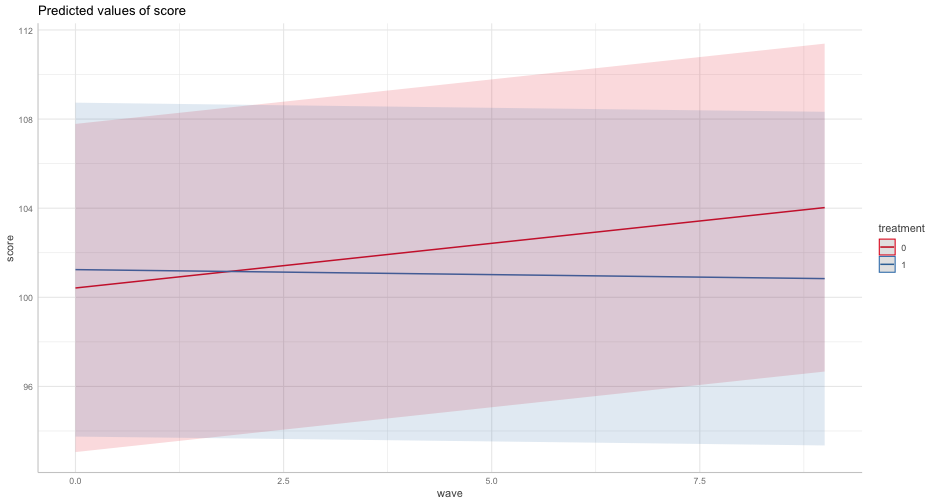
```r
library(ggeffects)
ggpredict(m2, "wave")
```

```
## # Predicted values of score
## # x = wave
## 
## x | Predicted |          95% CI
## -------------------------------
## 0 |    100.42 | [93.05, 107.78]
## 1 |    100.82 | [93.46, 108.18]
## 2 |    101.22 | [93.86, 108.58]
## 3 |    101.62 | [94.26, 108.98]
## 5 |    102.42 | [95.07, 109.78]
## 6 |    102.82 | [95.47, 110.18]
## 7 |    103.23 | [95.87, 110.58]
## 9 |    104.03 | [96.67, 111.39]
## 
## Adjusted for:
## * treatment =    0
## *     group = high
## *  prop_low = 0.30
## *       sid = 0 (population-level)
## *    school = 0 (population-level)
```

---
# Even automated plotting!

```r
ggpredict(m2, c("wave", "treatment")) %>% 
  plot()
```

![](w3p1_files/figure-html/unnamed-chunk-84-1.png)

---
# Individual observation
We can get these prediction intervals for specific levels also

```r
ggpredict(m2, "wave", condition = c(sid = 1, school = 1))
```

---
# All categorical groups
Note - things aren't perfect here, but it's still helpful.

```r
ggpredict(m2, c("wave", "treatment", "group"), 
          condition = c(sid = 1, school = 1)) %>% 
  plot()
```

![](w3p1_files/figure-html/unnamed-chunk-86-1.png)

---
class: inverse-green middle

# Next time
* Digging into the variance-covariance matrix of the random effects

* Finally discussing Gelman & Hill notation in more depth

* Homework 1 is due