Variance-Covariance Matrices

class: center, middle, inverse, title-slide

# Variance-Covariance Matrices
### Daniel Anderson
### Week 4

---

layout: true

---
# Agenda

* Review some notation

* Unstructured VCV Matrices and alternatives

---
# Learning Objectives

* Gain a deeper understanding of how the residual structure is different in multilevel models

* Understand that there are methods for changing the residual structure, and understand when and why this might be preferable

* Be able to implement alternative methods using [**{nlme}**](https://cran.r-project.org/web/packages/nlme/)

---
class: inverse-blue middle

# Notation
### Reviewing some Gelman and Hill notation

---
# Data
Let's start by using the *sleepstudy* data from **{lme4}**.

```r
library(lme4)
head(sleepstudy)
```

```
##   Reaction Days Subject
## 1 249.5600    0     308
## 2 258.7047    1     308
## 3 250.8006    2     308
## 4 321.4398    3     308
## 5 356.8519    4     308
## 6 414.6901    5     308
```

---
# Translate
Translate the following model into `lme4::lmer()` syntax

$$
`\begin{aligned}
  \operatorname{Reaction}_{i}  &\sim N \left(\alpha_{j[i]}, \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right)
    \text{, for Subject j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(Reaction ~ 1 + (1|Subject), data = sleepstudy)
```

---
# More complicated

Translate this equation into `lme4::lmer()` syntax

$$
`\begin{aligned}
  \operatorname{Reaction}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1}(\operatorname{Days}), \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right)
    \text{, for Subject j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(Reaction ~ Days + (1|Subject), data = sleepstudy)
```

---
# Even more complicated

Translate this equation into `lme4::lmer()` syntax

$$
`\begin{aligned}
  \operatorname{Reaction}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{Days}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for Subject j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(Reaction ~ Days + (Days|Subject), data = sleepstudy)
```

---
# New data

```r
sim3 <- read_csv(here::here("data", "sim3level.csv"))
sim3
```

```
## # A tibble: 570 x 6
##        Math ActiveTime ClassSize Classroom School StudentID
##       <dbl>      <dbl>     <dbl>     <dbl> <chr>      <dbl>
##  1 55.42604 0.06913359        18         1 Sch1           1
##  2 54.34306 0.08462063        18         1 Sch1           2
##  3 61.42570 0.1299456         18         1 Sch1           3
##  4 56.12271 0.7461320         18         1 Sch1           4
##  5 53.34900 0.03887918        18         1 Sch1           5
##  6 57.99773 0.6856354         18         1 Sch1           6
##  7 54.46326 0.1439774         18         1 Sch1           7
##  8 64.20517 0.8910800         18         1 Sch1           8
##  9 54.49117 0.08963612        18         1 Sch1           9
## 10 57.87599 0.03773272        18         1 Sch1          10
## # … with 560 more rows
```

.footnote[Data obtained [here](http://alexanderdemos.org/Mixed5.html)]

---
# A bit of a problem

```r
sim3 %>% 
  count(Classroom, School)
```

```
## # A tibble: 30 x 3
##    Classroom School     n
##        <dbl> <chr>  <int>
##  1         1 Sch1      18
##  2         1 Sch2      18
##  3         1 Sch3      19
##  4         2 Sch1      14
##  5         2 Sch2      18
##  6         2 Sch3      24
##  7         3 Sch1      20
##  8         3 Sch2      15
##  9         3 Sch3      20
## 10         4 Sch1      14
## # … with 20 more rows
```

---
# Make classroom unique
We could handle this with our model syntax, but nested IDs like this always makes me nervous. Let's make them unique.

```r
sim3 <- sim3 %>% 
  mutate(class_id = paste0("class", Classroom, ":", School))
sim3
```

```
## # A tibble: 570 x 7
##        Math ActiveTime ClassSize Classroom School StudentID class_id   
##       <dbl>      <dbl>     <dbl>     <dbl> <chr>      <dbl> <chr>      
##  1 55.42604 0.06913359        18         1 Sch1           1 class1:Sch1
##  2 54.34306 0.08462063        18         1 Sch1           2 class1:Sch1
##  3 61.42570 0.1299456         18         1 Sch1           3 class1:Sch1
##  4 56.12271 0.7461320         18         1 Sch1           4 class1:Sch1
##  5 53.34900 0.03887918        18         1 Sch1           5 class1:Sch1
##  6 57.99773 0.6856354         18         1 Sch1           6 class1:Sch1
##  7 54.46326 0.1439774         18         1 Sch1           7 class1:Sch1
##  8 64.20517 0.8910800         18         1 Sch1           8 class1:Sch1
##  9 54.49117 0.08963612        18         1 Sch1           9 class1:Sch1
## 10 57.87599 0.03773272        18         1 Sch1          10 class1:Sch1
## # … with 560 more rows
```

---
# New model

Translate this equation into code

$$
`\begin{aligned}
  \operatorname{Math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i]}(\operatorname{ActiveTime}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for class_id j = 1,} \dots \text{,J} \\    \alpha_{k}  &\sim N \left(\mu_{\alpha_{k}}, \sigma^2_{\alpha_{k}} \right)
    \text{, for School k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(Math ~ ActiveTime + (ActiveTime|class_id) + (1|School),
     data = sim3)
```

---
# This one
What about this one?

$$
\small
`\begin{aligned}
  \operatorname{Math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{ActiveTime}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{ClassSize}) \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for class_id j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{k}} \\
      &\mu_{\beta_{1k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}}
  \end{array}
\right)
 \right)
    \text{, for School k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(Math ~ ActiveTime + ClassSize + 
       (ActiveTime|class_id) + (ActiveTime|School),
     data = sim3)
```

---
# Last one

What about this one?

$$
\small
`\begin{aligned}
  \operatorname{Math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{ActiveTime}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1k[i]}^{\alpha}(\operatorname{ClassSize}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{ClassSize})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for class_id j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\gamma_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{k}} \\
      &\mu_{\beta_{1k}} \\
      &\mu_{\gamma_{1k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} & \rho_{\alpha_{k}\gamma_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}} & \rho_{\beta_{1k}\gamma_{1k}} \\ 
     \rho_{\gamma_{1k}\alpha_{k}} & \rho_{\gamma_{1k}\beta_{1k}} & \sigma^2_{\gamma_{1k}}
  \end{array}
\right)
 \right)
    \text{, for School k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(Math ~ ActiveTime * ClassSize + 
       (ActiveTime|class_id) + (ActiveTime + ClassSize|School),
     data = sim3)
```

---
class: inverse-blue middle

# Residual structures

---
# Data
[Willett, 1988](https://www.jstor.org/stable/1167368?seq=1#metadata_info_tab_contents)

* `$n$` = 35 people
* Each completed a cognitive inventory on "opposites naming"
* At first time point, participants also completed a general cognitive measure

---
# Read in data

```r
willett <- read_csv(here::here("data", "willett-1988.csv"))
willett
```

```
## # A tibble: 140 x 4
##       id  time   opp   cog
##    <dbl> <dbl> <dbl> <dbl>
##  1     1     0   205   137
##  2     1     1   217   137
##  3     1     2   268   137
##  4     1     3   302   137
##  5     2     0   219   123
##  6     2     1   243   123
##  7     2     2   279   123
##  8     2     3   302   123
##  9     3     0   142   129
## 10     3     1   212   129
## # … with 130 more rows
```

---
# Standard OLS

* We have four observations per participant.

* If we fit a standard OLS model, it would look like this

```r
bad <- lm(opp ~ time, data = willett)
summary(bad)
```

```
## 
## Call:
## lm(formula = opp ~ time, data = willett)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -88.374 -25.584   1.186  28.926  64.746 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  164.374      5.035   32.65   <2e-16 ***
## time          26.960      2.691   10.02   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 35.6 on 138 degrees of freedom
## Multiple R-squared:  0.421,	Adjusted R-squared:  0.4168 
## F-statistic: 100.3 on 1 and 138 DF,  p-value: < 2.2e-16
```

---
# Assumptions
As we discussed previously, this model looks like this

$$
\operatorname{opp} = \alpha + \beta_{1}(\operatorname{time}) + \epsilon
$$

where

$$
\epsilon \sim \left(0, \sigma \right)
$$

---
# Individual level residuals
We can expand our notation, so it looks like a multivariate normal distribution

$$
`\begin{equation}
  \left(
    \begin{array}{c}
      \epsilon_1 \\\
      \epsilon_2 \\\
      \epsilon_3 \\\
      \vdots \\\
      \epsilon_n
    \end{array}
  \right)
\sim MVN
  \left(
    \left[
      \begin{array}{c}
        0\\\
        0\\\
        0\\\
        \vdots \\\
        0
    \end{array}
    \right],
    \left[
      \begin{array}{ccccc}
        \sigma_{\epsilon} & 0 & 0 & \dots & 0 \\\
        0 & \sigma_{\epsilon} & 0 & 0 & 0 \\\
        0 & 0 & \sigma_{\epsilon} & 0 & 0 \\\
        \vdots & 0 & 0 & \ddots & \vdots \\\
        0 & 0 & 0 & \dots & \sigma_{\epsilon}
      \end{array}
    \right]
  \right)
\end{equation}`
$$

This is where the `$i.i.d.$` part comes in. The residuals are assumed `$i$`ndependent and `$i$`dentically `$d$`istributed.

---
# Multilevel model
Very regularly, there are reasons to believe the `$i.i.d.$` assumption is violated. Consider our current case, with 4 time points for each individual.

* Is an observation for one time point for one individual *independent* from the other observations for that individual?

--
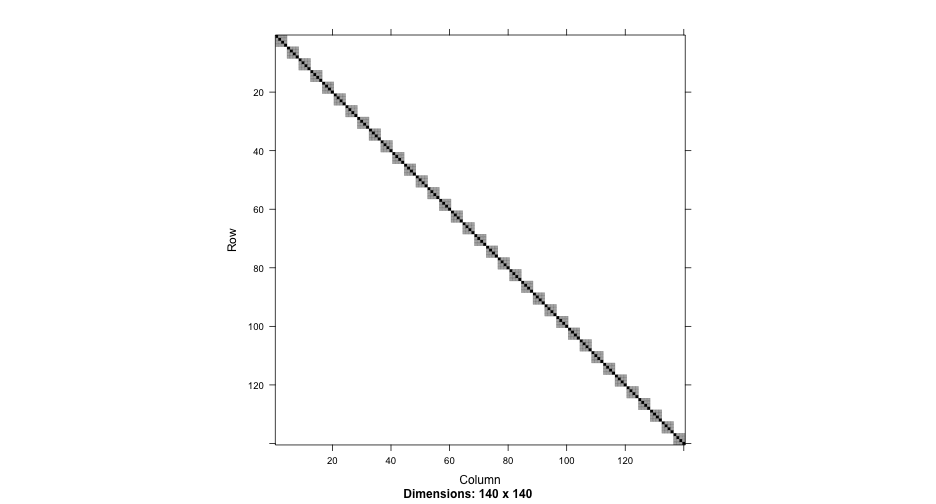
* Rather than estimating a single residual variance, we estimate an additional components associated with individuals, leading to a *block* diagonal structure

---
# Block diagonal

.small70[
$$
`\begin{equation}
  \left(
    \begin{array}{c}
      \epsilon_{11} \\
      \epsilon_{12} \\
      \epsilon_{13} \\
      \epsilon_{14} \\
      \epsilon_{21} \\
      \epsilon_{22} \\
      \epsilon_{23} \\
      \epsilon_{24} \\
      \vdots \\
      \epsilon_{n1} \\
      \epsilon_{n2} \\
      \epsilon_{n3} \\
      \epsilon_{n4}
    \end{array}
  \right)
\sim
  \left(
    \left[
      \begin{array}{c}
        \\
        0\\
        0\\
        0\\
        0\\
        0\\
        0\\
        0\\
        0\\
        \vdots \\
        0\\
        0\\
        0\\
        0
      \end{array}
    \right],
    \left[
      \begin{array}{{@{}*{13}c@{}}}
      \\
        \sigma_{11} & \sigma_{12} & \sigma_{13} & \sigma_{14} & 0 & 0 & 0 & 0 & \dots  & 0 & 0 & 0 & 0 \\
        \sigma_{21} & \sigma_{22} & \sigma_{23} & \sigma_{24} & 0 & 0 & 0 & 0 & \dots  & 0 & 0 & 0 & 0 \\
        \sigma_{31} & \sigma_{32} & \sigma_{33} & \sigma_{34} & 0 & 0 & 0 & 0 & \dots  & 0 & 0 & 0 & 0 \\
        \sigma_{41} & \sigma_{42} & \sigma_{43} & \sigma_{44} & 0 & 0 & 0 & 0 & \dots  & 0 & 0 & 0 & 0 \\
        0 & 0 & 0 & 0 & \sigma_{11} & \sigma_{12} & \sigma_{13} & \sigma_{14} & \dots  & 0 & 0 & 0 & 0 \\
        0 & 0 & 0 & 0 & \sigma_{21} & \sigma_{22} & \sigma_{23} & \sigma_{24} & \dots  & 0 & 0 & 0 & 0 \\
        0 & 0 & 0 & 0 & \sigma_{31} & \sigma_{32} & \sigma_{33} & \sigma_{34} & \dots  & 0 & 0 & 0 & 0 \\
        0 & 0 & 0 & 0 & \sigma_{41} & \sigma_{42} & \sigma_{43} & \sigma_{44} & \dots  & 0 & 0 & 0 & 0 \\
        \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\
        0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \dots & \sigma_{11} & \sigma_{12} & \sigma_{13} & \sigma_{14} \\
        0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \dots & \sigma_{21} & \sigma_{22} & \sigma_{23} & \sigma_{24} \\
        0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \dots & \sigma_{31} & \sigma_{32} & \sigma_{33} & \sigma_{34} \\
        0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \dots & \sigma_{41} & \sigma_{42} & \sigma_{43} & \sigma_{44}
      \end{array}
    \right]
  \right)
\end{equation}`
$$
]

--
Correlations for  off-diagonals estimated

--
Same variance components for all blocks

--
Out-of-block diagonals are still zero

---
# Homogeneity of variance
As mentioned on the previous slide, we assume the same variance components across all student

This is referred to as the homogeneity of variance assumption - although the block (often referred to as the composite residual) may be heteroscedastic and dependent **within** a grouping factor (i.e., people) the entire error structure is repeated identically across units (i.e., people)

---
# Block diagonal
Because of the homogeneity of variance assumption, we can re-express our block diagonal design as follows

$$
`\begin{equation}
r \sim N \left(\boldsymbol{0}, 
  \left[
    \begin{array}{ccccc}
      \boldsymbol{\Sigma_r} & \boldsymbol{0} & \boldsymbol{0} & \dots & \boldsymbol{0} \\
      \boldsymbol{0} & \boldsymbol{\Sigma_r} & \boldsymbol{0} & \dots & \boldsymbol{0} \\
      \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{\Sigma_r} &  \dots & \boldsymbol{0} \\
      \vdots & \vdots & \vdots & \ddots & \vdots & \\
      \boldsymbol{0} & \boldsymbol{0} &  \boldsymbol{0} & \dots & \boldsymbol{\Sigma_r}
    \end{array}
  \right]
\right)
\end{equation}`
$$
---
# Composite residual
We then define the composite residual, which is common across units

$$
`\begin{equation}
  \boldsymbol{\Sigma_r} = \left[
    \begin{array}{cccc}
      \sigma_{11} & \sigma_{12} & \sigma_{13} & \sigma_{14} \\
      \sigma_{21} & \sigma_{22} & \sigma_{23} & \sigma_{24} \\
      \sigma_{31} & \sigma_{32} & \sigma_{33} & \sigma_{34} \\
      \sigma_{41} & \sigma_{42} & \sigma_{43} & \sigma_{44}
    \end{array}
  \right]
\end{equation}`
$$

---
# Let's try!

Let's fit a parallel slopes model with the Willett data. You try first.

```r
w0 <- lmer(opp ~ time + (1|id), willett)
```

--
What does the residual variance-covariance look like? Let's use **sundry** to pull it

```r
library(sundry)
w0_rvcv <- pull_residual_vcov(w0)
```

---
# Image
Sparse matrix - we can view it with `image()`

```r
image(w0_rvcv)
```

![](w5p1_files/figure-html/unnamed-chunk-22-1.png)

---
# Pull first few rows/cols

```r
w0_rvcv[1:8, 1:8]
```

```
## 8 x 8 sparse Matrix of class "dgCMatrix"
##           1         2         3         4         5         6         7         8
## 1 1280.7065  904.8054  904.8054  904.8054    .         .         .         .     
## 2  904.8054 1280.7065  904.8054  904.8054    .         .         .         .     
## 3  904.8054  904.8054 1280.7065  904.8054    .         .         .         .     
## 4  904.8054  904.8054  904.8054 1280.7065    .         .         .         .     
## 5    .         .         .         .      1280.7065  904.8054  904.8054  904.8054
## 6    .         .         .         .       904.8054 1280.7065  904.8054  904.8054
## 7    .         .         .         .       904.8054  904.8054 1280.7065  904.8054
## 8    .         .         .         .       904.8054  904.8054  904.8054 1280.7065
```

---
# Structure
On the previous slide, note the values on the diagonal are all the same, as are all the off-diagonals

* This is because we've only estimated one additional variance component

---
# Understanding these numbers
Let's look at the model output

```r
arm::display(w0)
```

```
## lmer(formula = opp ~ time + (1 | id), data = willett)
##             coef.est coef.se
## (Intercept) 164.37     5.78 
## time         26.96     1.47 
## 
## Error terms:
##  Groups   Name        Std.Dev.
##  id       (Intercept) 30.08   
##  Residual             19.39   
## ---
## number of obs: 140, groups: id, 35
## AIC = 1308.3, DIC = 1315.9
## deviance = 1308.1
```

---
The diagonal values were `$1280.7065389$` while the off diagonal values were `$904.8053852$`

Let's extract the variance components from our model.

```r
vars_w0 <- as.data.frame(VarCorr(w0))
vars_w0
```

```
##        grp        var1 var2     vcov    sdcor
## 1       id (Intercept) <NA> 904.8054 30.07998
## 2 Residual        <NA> <NA> 375.9012 19.38817
```

Notice anything?

The diagonals are given by `sum(vars_w0)$vcov` while the off-diagonals are just the intercept variance

---
# Including more complexity

Try estimating this model now, then look at the residual variance-covariance matrix again

$$
`\begin{aligned}
  \operatorname{opp}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{time}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for id j = 1,} \dots \text{,J}
\end{aligned}`
$$

---
# The composite residual

```r
w1 <- lmer(opp ~ time + (time|id), willett)
w1_rvcv <- pull_residual_vcov(w1)
w1_rvcv[1:4, 1:4]
```

```
## 4 x 4 sparse Matrix of class "dgCMatrix"
##           1         2         3         4
## 1 1358.2469 1019.5095  840.2515  660.9934
## 2 1019.5095 1132.1294  925.7905  878.9310
## 3  840.2515  925.7905 1170.8089 1096.8686
## 4  660.9934  878.9310 1096.8686 1474.2856
```

--
### Unstructured

The model we fit has an *unstructured* variance co-variance matrix. While each
block is the same, every element of the block is now estimated.

---
# What are these numbers?
They are the variance components, re-expressed as a composite residual

--
The diagonal is given by

$$
`\begin{equation}
\sigma^2 + \sigma^2_{\alpha_j} + 2\sigma^2_{01}w_i + \sigma^2_{\beta_1}w^2_i 
\end{equation}`
$$

where `$w$` represents the given wave (for our example)

--
Let's do this "by hand"

---
# Get the pieces

```r
vars_w1 <- as.data.frame(VarCorr(w1))

# get the pieces
int_var <- vars_w1$vcov[1]
slope_var <- vars_w1$vcov[2]
covar <- vars_w1$vcov[3]
residual <- vars_w1$vcov[4]
```

---
# Calculate

```r
diag(w1_rvcv[1:4, 1:4])
```

```
## [1] 1358.247 1132.129 1170.809 1474.286
```

```r
residual + int_var
```

```
## [1] 1358.247
```

```r
residual + int_var + 2*covar + slope_var
```

```
## [1] 1132.129
```

```r
residual + int_var + (2*covar)*2 + slope_var*2^2
```

```
## [1] 1170.809
```

```r
residual + int_var + (2*covar)*3 + slope_var*3^2
```

```
## [1] 1474.286
```

---
# Why?
What was the point of doing that by hand?

![](https://media1.popsugar-assets.com/files/thumbor/2qfH3BIwMUci7X3COzTN2VCEPL0/fit-in/728xorig/filters:format_auto-!!-:strip_icc-!!-/2014/07/09/780/n/1922283/4c633a9489b97031_tumblr_inline_mn9lfioyVS1qz4rgp/i/He-Basically-Invented-Side-Eye-Move.gif)

I don't really care about the equations - the point is, they're just transformations of the variance components

---
# Off-diagonals

The off-diagonals are given by

$$
`\begin{equation}
\sigma^2_{\alpha_j} + \sigma_{01}(t_i + t_i') + \sigma^2_{\beta_1}t_it_i'
\end{equation}`
$$

---
# Calculate a few

```r
w1_rvcv[1:4, 1:4]
```

```r
int_var + covar*(1 + 0) + slope_var*1*0
```

```
## [1] 1019.51
```

```r
int_var + covar*(2 + 1) + slope_var*2*1
```

```
## [1] 925.7905
```

```r
int_var + covar*(3 + 2) + slope_var*3*2
```

```
## [1] 1096.869
```

```r
int_var + covar*(2 + 0) + slope_var*2*0
```

```
## [1] 840.2515
```

---
class: inverse-red middle
# Positing other structures

---
# The possibilities
There are a number of alternative structures. We'll talk about a few here.

--
If you want to go deeper, I suggest Singer & Willett, Chapter 7

--
Code to fit models with each type of structure, using the same Willett data we're using today, is available [here](https://stats.idre.ucla.edu/r/examples/alda/r-applied-longitudinal-data-analysis-ch-7/)

---
# Structures we'll fit

* Unstructured (default with **lme4**, we've already seen this)

* Variance components (no off-diagonals)

* Autoregressive

* Heterogeneous autoregressive

* Toeplitz

--
Note this is just a sampling. Other structures are possible.

--
Outside of *unstructured* & *variance component only* models, we'll need to use the **nlme** package

--
We could also use Bayes, as we'll get to in a few weeks.

---
class: inverse-orange middle
# Variance component only

---
# The model
Generally, in a model like the Willett data, we would estimate intercept variance, and maybe slope variance.

--
We saw earlier how these combine to create the residual variance-covariance matrix

--
Alternatively, we can estimate separate variances at each time point

$$
`\begin{equation}
  \boldsymbol{\Sigma_r} = \left[
    \begin{array}{cccc}
      \sigma^2_1 & 0 & 0 & 0 \\
      0 & \sigma^2_2 & 0 & 0 \\
      0 & 0 & \sigma^2_3 & 0 \\
      0 & 0 & 0 & \sigma^2_4
    \end{array}
  \right]
\end{equation}`
$$

---
# One-hot encoding

First, use one-hot encoding for time

Same as dummy-coding, but you use *all* the levels.

```r
w <- willett %>% 
  mutate(t0 = ifelse(time == 0, 1, 0),
         t1 = ifelse(time == 1, 1, 0),
         t2 = ifelse(time == 2, 1, 0),
         t3 = ifelse(time == 3, 1, 0))
w
```

```
## # A tibble: 140 x 8
##       id  time   opp   cog    t0    t1    t2    t3
##    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
##  1     1     0   205   137     1     0     0     0
##  2     1     1   217   137     0     1     0     0
##  3     1     2   268   137     0     0     1     0
##  4     1     3   302   137     0     0     0     1
##  5     2     0   219   123     1     0     0     0
##  6     2     1   243   123     0     1     0     0
##  7     2     2   279   123     0     0     1     0
##  8     2     3   302   123     0     0     0     1
##  9     3     0   142   129     1     0     0     0
## 10     3     1   212   129     0     1     0     0
## # … with 130 more rows
```

---
# Alternative creation
The `model.matrix()` function automatically dummy-codes factors.

```r
model.matrix( ~ 0 + factor(time), data = willett) %>% 
  head()
```

```
##   factor(time)0 factor(time)1 factor(time)2 factor(time)3
## 1             1             0             0             0
## 2             0             1             0             0
## 3             0             0             1             0
## 4             0             0             0             1
## 5             1             0             0             0
## 6             0             1             0             0
```

--
Could be helpful if time is coded in a more complicated way

---
# Fit the model

```r
varcomp <- lmer(opp ~  time + (0 + t0 + t1 + t2 + t3 || id), w)
summary(varcomp)
```

```
## Linear mixed model fit by REML ['lmerMod']
## Formula: opp ~ time + ((0 + t0 | id) + (0 + t1 | id) + (0 + t2 | id) +      (0 + t3 | id))
##    Data: w
## 
## REML criterion at convergence: 1387.2
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.70477 -0.50440  0.02222  0.58653  1.37347 
## 
## Random effects:
##  Groups   Name Variance Std.Dev.
##  id       t0   671.8    25.92   
##  id.1     t1   478.9    21.88   
##  id.2     t2   643.8    25.37   
##  id.3     t3   777.7    27.89   
##  Residual      625.0    25.00   
## Number of obs: 140, groups:  id, 35
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  164.429      5.007  32.839
## time          26.925      2.758   9.762
## 
## Correlation of Fixed Effects:
##      (Intr)
## time -0.801
```

---
# Estimation
* Estimates the variance at each timepoint independently (`||`)

+ In other words, no correlation is estimated

```r
sundry::pull_residual_vcov(varcomp)[1:4, 1:4]
```

```
## 4 x 4 sparse Matrix of class "dgCMatrix"
##         1        2        3        4
## 1 1296.75    .        .        .    
## 2    .    1103.838    .        .    
## 3    .       .     1268.773    .    
## 4    .       .        .     1402.641
```

---
# Thinking deeper

How reasonable is it to assume the variance at one time point?

--
In most cases, probably not very.

--
.realbig[BUT]

--
Sometimes we can't reliably estimate the covariances, so this helps simplify our model so it's estimable, even if the assumptions we're making are stronger.

---
# Fully unstructured
* We could estimate separate variance *and* all the covariances - this is just a *really* complicated model

* By default, **lme4** will actually try to prevent you from doing this

```r
fully_unstructured <- lmer(opp ~  time + 
                             (0 + t0 + t1 + t2 + t3 | id), 
                           data = w)
```

```
## Error: number of observations (=140) <= number of random effects (=140) for term (0 + t0 + t1 + t2 + t3 | id); the random-effects parameters and the residual variance (or scale parameter) are probably unidentifiable
```

---
# Ignore checks

Number of random effects == observations.

We can still estimate, just tell the model to ignore this check

```r
fully_unstructured <- lmer(
  opp ~  time + (0 + t0 + t1 + t2 + t3 | id), 
  data = w,
* control = lmerControl(check.nobs.vs.nRE = "ignore")
) 
```

---

```r
arm::display(fully_unstructured)
```

```
## lmer(formula = opp ~ time + (0 + t0 + t1 + t2 + t3 | id), data = w, 
##     control = lmerControl(check.nobs.vs.nRE = "ignore"))
##             coef.est coef.se
## (Intercept) 165.83     5.87 
## time         26.58     2.12 
## 
## Error terms:
##  Groups   Name Std.Dev. Corr           
##  id       t0   34.42                   
##           t1   31.58    0.90           
##           t2   34.16    0.78 0.94      
##           t3   35.95    0.46 0.75 0.88 
##  Residual      11.09                   
## ---
## number of obs: 140, groups: id, 35
## AIC = 1289.4, DIC = 1280.3
## deviance = 1271.9
```

---
# Terminology

* What **lme4** fits by default is generally referred to as an *unstructured* variance-covariance matrix.

* This means the random effect variances and covariances are all estimated

* The previous model I am referring to as *fully* unstructured, because we estimate seperate variances at each time point

* Some might not make this distinction, so just be careful when people use this term

---
class: inverse-orange middle
# Autoregressive

---
# Autoregressive
* There are many types of autoregressive structures
  + If you took a class on time-series data you'd learn about others
  
* What we'll talk about is referred to as an AR1 structure

* Variances (on the diagonal) are constant

* Includes constant "band-diagonals"

---
# Autoregressive

$$
`\begin{equation}
  \boldsymbol{\Sigma_r} = \left[
    \begin{array}{cccc}
      \sigma^2 & \sigma^2\rho & \sigma^2\rho^2 & \sigma^2\rho^3 \\
      \sigma^2\rho & \sigma^2 & \sigma^2\rho & \sigma^2\rho^2 \\
      \sigma^2\rho^2 & \sigma^2\rho & \sigma^2 & \sigma^2\rho \\
      \sigma^2\rho^3 & \sigma^2\rho^2 & \sigma^2\rho & \sigma^2
    \end{array}
  \right]
\end{equation}`
$$
* Each band is forced to be lower than the prior by a constant fraction
  + estimated autocorrelation parameter `$\rho$`. The error variance is multiplied by `$\rho$` for the first diagonal, by `$\rho^2$` for the second, etc.

* Uses only two variance components

---
# Fit

First load **nlme**

```r
library(nlme)
```

--
We'll use the `gls()` function. The interface is, overall, fairly similar to **lme4**

```r
ar <- gls(opp ~ time, 
          data = willett,
          correlation = corAR1(form = ~ 1|id))
```

---
# Summary
Notice, you're not  estimating random effect variances, just an alternative residual covariance structure

```r
summary(ar)
```

```
## Generalized least squares fit by REML
##   Model: opp ~ time 
##   Data: willett 
##        AIC      BIC    logLik
##   1281.465 1293.174 -636.7327
## 
## Correlation Structure: AR(1)
##  Formula: ~1 | id 
##  Parameter estimate(s):
##       Phi 
## 0.8249118 
## 
## Coefficients:
##                 Value Std.Error  t-value p-value
## (Intercept) 164.33842  6.136372 26.78104       0
## time         27.19786  1.919857 14.16661       0
## 
##  Correlation: 
##      (Intr)
## time -0.469
## 
## Standardized residuals:
##         Min          Q1         Med          Q3         Max 
## -2.42825488 -0.71561388  0.03192973  0.78792605  1.76110779 
## 
## Residual standard error: 36.37938 
## Degrees of freedom: 140 total; 138 residual
```

---
# Extract composite residual

```r
cm_ar <- corMatrix(ar$modelStruct$corStruct) # all of them
cr_ar <- cm_ar[[1]] # just the first (they're all the same)
cr_ar
```

```
##           [,1]      [,2]      [,3]      [,4]
## [1,] 1.0000000 0.8249118 0.6804795 0.5613356
## [2,] 0.8249118 1.0000000 0.8249118 0.6804795
## [3,] 0.6804795 0.8249118 1.0000000 0.8249118
## [4,] 0.5613356 0.6804795 0.8249118 1.0000000
```

Multiply the correlation matrix by the model residual variance to get the covariance matrix

```r
cr_ar * sigma(ar)^2
```

```
##           [,1]      [,2]      [,3]      [,4]
## [1,] 1323.4596 1091.7375  900.5872  742.9050
## [2,] 1091.7375 1323.4596 1091.7375  900.5872
## [3,]  900.5872 1091.7375 1323.4596 1091.7375
## [4,]  742.9050  900.5872 1091.7375 1323.4596
```

---
# Confirming calculations

```r
sigma(ar)^2
```

```
## [1] 1323.46
```

```r
sigma(ar)^2*0.8249118
```

```
## [1] 1091.737
```

```r
sigma(ar)^2*0.8249118^2
```

```
## [1] 900.5871
```

```r
sigma(ar)^2*0.8249118^3
```

```
## [1] 742.9049
```

---
# Heterogenous autoregressive
* Same as autorgressive but allows each variance to differ

* Still one `$\rho$` estimated

+ Same "decay" across band diagonals

* Band diagonals no longer equivalent, because different variances

---
# Heterogenous autoregressive

$$
`\begin{equation}
  \boldsymbol{\Sigma_r} = \left[
    \begin{array}{cccc}
      \sigma^2_1 & \sigma_1\sigma_2\rho & \sigma_1\sigma_3\rho^2 & \sigma_1\sigma_4\rho^2 \\
      \sigma_2\sigma_1\rho & \sigma^2_2 & \sigma_2\sigma_3\rho & \sigma_2\sigma_4\rho^2 \\
      \sigma_3\sigma_1\rho^2 & \sigma_3\sigma_2\rho & \sigma^2_3 & \sigma_3\sigma_4\rho \\
      \sigma_4\sigma_1\rho^3 & \sigma_4\sigma_2\rho^2 & \sigma_4\sigma_3\rho & \sigma^2_4
    \end{array}
  \right]
\end{equation}`
$$

---
# Fit
Note - `varIdent` specifies different variances for each wave (variances of the [identity matrix](https://en.wikipedia.org/wiki/Identity_matrix))

```r
har <- gls(
  opp ~ time,
  data = willett,
  correlation = corAR1(form = ~ 1|id),
  weights = varIdent(form = ~1|time)
)
```

---
# Summary

```r
summary(har)
```

```
## Generalized least squares fit by REML
##   Model: opp ~ time 
##   Data: willett 
##       AIC     BIC    logLik
##   1285.76 1306.25 -635.8798
## 
## Correlation Structure: AR(1)
##  Formula: ~1 | id 
##  Parameter estimate(s):
##       Phi 
## 0.8173622 
## Variance function:
##  Structure: Different standard deviations per stratum
##  Formula: ~1 | time 
##  Parameter estimates:
##        0        1        2        3 
## 1.000000 0.915959 0.985068 1.045260 
## 
## Coefficients:
##                 Value Std.Error  t-value p-value
## (Intercept) 164.63344  5.959533 27.62523       0
## time         27.11552  1.984807 13.66154       0
## 
##  Correlation: 
##      (Intr)
## time -0.45 
## 
## Standardized residuals:
##         Min          Q1         Med          Q3         Max 
## -2.45009645 -0.74377345  0.02395442  0.82305791  1.81833605 
## 
## Residual standard error: 36.17549 
## Degrees of freedom: 140 total; 138 residual
```

---
# Extract/compute composite residual

The below is fairly complicated, but you can work it out if you go line by line

```r
cm_har <- corMatrix(har$modelStruct$corStruct)[[1]] 
var_struct <- har$modelStruct$varStruct
vars <- coef(var_struct, unconstrained = FALSE, allCoef = TRUE)
vars <- matrix(vars, ncol = 1)

cm_har * sigma(har)^2 * 
  (vars %*% t(vars)) # multiply by a mat of vars
```

```
##           [,1]      [,2]      [,3]      [,4]
## [1,] 1308.6660  979.7593  861.2399  746.9588
## [2,]  979.7593 1097.9457  965.1295  837.0629
## [3,]  861.2399  965.1295 1269.8757 1101.3712
## [4,]  746.9588  837.0629 1101.3712 1429.8058
```

---
# Toeplitz

* Constant variance

* Has identical band-diagonals, like autoregressive

* Relaxes assumption of each band being a parallel by a common fraction of the prior band

+ Each band determined empirically by the data

--
A bit of a compromise between prior two

---
# Toeplitz

$$
`\begin{equation}
  \boldsymbol{\Sigma_r} = \left[
    \begin{array}{cccc}
      \sigma^2 & \sigma^2_1 & \sigma^2_2 & \sigma^2_3 \\
      \sigma^2_1 & \sigma^2 & \sigma^2_1 & \sigma^2_2 \\
      \sigma^2_2 & \sigma^2_1 & \sigma^2 & \sigma^2_1 \\
      \sigma^2_2 & \sigma^2_2 & \sigma^2_1 & \sigma^2
    \end{array}
  \right]
\end{equation}`
$$

--
## Fit

```r
toep <- gls(opp ~ time, 
            data = willett,
            correlation = corARMA(form = ~ 1|id, p = 3))
```

---
# Summary

```r
summary(toep)
```

```
## Generalized least squares fit by REML
##   Model: opp ~ time 
##   Data: willett 
##        AIC      BIC    logLik
##   1277.979 1295.543 -632.9896
## 
## Correlation Structure: ARMA(3,0)
##  Formula: ~1 | id 
##  Parameter estimate(s):
##       Phi1       Phi2       Phi3 
##  0.8039121  0.3665122 -0.3950326 
## 
## Coefficients:
##                 Value Std.Error  t-value p-value
## (Intercept) 165.11855  6.122841 26.96764       0
## time         26.91997  2.070391 13.00236       0
## 
##  Correlation: 
##      (Intr)
## time -0.507
## 
## Standardized residuals:
##         Min          Q1         Med          Q3         Max 
## -2.44029024 -0.71984566  0.01373249  0.77304950  1.75580973 
## 
## Residual standard error: 36.51965 
## Degrees of freedom: 140 total; 138 residual
```

---
# Extract/compute composite residual
Same as with autoregressive - just multiply the correlation matrix by the residual variance

```r
cr_toep <- corMatrix(toep$modelStruct$corStruct)[[1]] 
cr_toep * sigma(toep)^2
```

```
##           [,1]      [,2]      [,3]      [,4]
## [1,] 1333.6848 1105.7350  940.9241  634.8366
## [2,] 1105.7350 1333.6848 1105.7350  940.9241
## [3,]  940.9241 1105.7350 1333.6848 1105.7350
## [4,]  634.8366  940.9241 1105.7350 1333.6848
```

---
# Comparing fits

```r
library(performance)
compare_performance(ar, har, toep, w1, varcomp, fully_unstructured,
                    metrics = c("AIC", "BIC"),
                    rank = TRUE) %>% 
  as_tibble()
```

```
## Warning: Could not get model data.

## Warning: Could not get model data.

## Warning: Could not get model data.
```

```
## Warning: When comparing models, please note that probably not all models were fit from same data.
```

```
## # A tibble: 6 x 5
##   Name               Model        AIC      BIC Performance_Score
##   <chr>              <chr>      <dbl>    <dbl>             <dbl>
## 1 toep               gls     1277.979 1295.543         0.9907943
## 2 ar                 gls     1281.465 1293.174         0.9858555
## 3 w1                 lmerMod 1278.823 1296.473         0.9837572
## 4 har                gls     1285.760 1306.250         0.9176060
## 5 fully_unstructured lmerMod 1289.423 1327.664         0.8195083
## 6 varcomp            lmerMod 1401.215 1421.806         0
```

We have slight evidence here that the Toeplitz structure fits better than the standard unstructured version, which was slightly better than the autoregressive model.

---
# gls models

---
# lme4 models

<table class="table" style="width: auto !important; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:center;"> Standard </th>
   <th style="text-align:center;"> Var Comp </th>
   <th style="text-align:center;"> Fully Unstruc </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:center;"> 164.374 </td>
   <td style="text-align:center;"> 164.429 </td>
   <td style="text-align:center;"> 165.832 </td>
  </tr>
  <tr>
   <td style="text-align:left;">  </td>
   <td style="text-align:center;"> (6.119) </td>
   <td style="text-align:center;"> (5.007) </td>
   <td style="text-align:center;"> (5.867) </td>
  </tr>
  <tr>
   <td style="text-align:left;"> time </td>
   <td style="text-align:center;"> 26.960 </td>
   <td style="text-align:center;"> 26.925 </td>
   <td style="text-align:center;"> 26.585 </td>
  </tr>
  <tr>
   <td style="text-align:left;">  </td>
   <td style="text-align:center;"> (2.167) </td>
   <td style="text-align:center;"> (2.758) </td>
   <td style="text-align:center;"> (2.121) </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__(Intercept) </td>
   <td style="text-align:center;"> 34.623 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__(Intercept).time </td>
   <td style="text-align:center;"> -0.450 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__time </td>
   <td style="text-align:center;"> 11.506 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__Observation </td>
   <td style="text-align:center;"> 12.629 </td>
   <td style="text-align:center;"> 24.999 </td>
   <td style="text-align:center;"> 11.087 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__t0 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 25.919 </td>
   <td style="text-align:center;"> 34.424 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__t1 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 21.883 </td>
   <td style="text-align:center;"> 31.582 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__t2 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 25.373 </td>
   <td style="text-align:center;"> 34.155 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> sd__t3 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 27.887 </td>
   <td style="text-align:center;"> 35.947 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__t0.t1 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 0.899 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__t0.t2 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 0.784 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__t0.t3 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 0.455 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__t1.t2 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 0.945 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> cor__t1.t3 </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;">  </td>
   <td style="text-align:center;"> 0.754 </td>
  </tr>
  <tr>
   <td style="text-align:left;box-shadow: 0px 1px"> cor__t2.t3 </td>
   <td style="text-align:center;box-shadow: 0px 1px">  </td>
   <td style="text-align:center;box-shadow: 0px 1px">  </td>
   <td style="text-align:center;box-shadow: 0px 1px"> 0.881 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> AIC </td>
   <td style="text-align:center;"> 1278.8 </td>
   <td style="text-align:center;"> 1401.2 </td>
   <td style="text-align:center;"> 1289.4 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> BIC </td>
   <td style="text-align:center;"> 1296.5 </td>
   <td style="text-align:center;"> 1421.8 </td>
   <td style="text-align:center;"> 1327.7 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Log.Lik. </td>
   <td style="text-align:center;"> -633.411 </td>
   <td style="text-align:center;"> -693.607 </td>
   <td style="text-align:center;"> -631.711 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> REMLcrit </td>
   <td style="text-align:center;"> 1266.823 </td>
   <td style="text-align:center;"> 1387.215 </td>
   <td style="text-align:center;"> 1263.423 </td>
  </tr>
</tbody>
</table>

---
class: inverse-red middle
# Stepping back
### Why do we care about all of this?

---
# Overfitting

* If a simpler model fits the data just as well, it should be preferred

* Models that are overfit have "learned too much" from the data and won't generalize well

* Can think of it as fitting to the errors in the data, rather than the "true" patterns found in the population

---
# Convergence issues

* As your models get increasingly complicated, you're likely to run into convergence issues.

* Simplifying your residual variance-covariance structure may help 
  + Keeps the basic model structure intact

--
Aside - see [here](http://bbolker.github.io/mixedmodels-misc/glmmFAQ.html#troubleshooting) for convergence troubleshooting with **lme4**. The `allFit()` function is often helpful but very computationally intensive.

---
# Summary
* As is probably fairly evident from the code - there are many more structures you could explore. However, most are not implemented through **lme4**.

* Simplifying the residual variance-covariance can sometimes lead to better fitting models

* May also be helpful with convergence and avoid overfitting

---
class: inverse-green middle
# Now
## Homework 2
### Next time: Modeling growth (part 1)