Modeling Growth 1

class: center, middle, inverse, title-slide

# Modeling Growth 1
### Daniel Anderson
### Week 5

---

layout: true

---
# Agenda
* More practice with equation/models

* Thinking flexibly about time

+ Coefficient interpretation by time coding
  
* A few methods for handling non-linearity

--
.realbig[Note]

The last bullet is not necessarily specific to growth models

---
class: inverse-blue middle
# Equation/model practice

---
# The data
Please load the following data

```r
library(tidyverse)
d <- read_csv(here::here("data", "longitudinal-sim.csv"))
```

---
# Model 1
Please translate the following model into `lme4::lmer()` code

$$
`\begin{aligned}
  \operatorname{g5\_spring}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1}(\operatorname{g4\_spring}) + \beta_{2}(\operatorname{g3\_spring}), \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right)
    \text{, for scid j = 1,} \dots \text{,J} \\
    \alpha_{k}  &\sim N \left(\mu_{\alpha_{k}}, \sigma^2_{\alpha_{k}} \right)
    \text{, for distid k = 1,} \dots \text{,K}
\end{aligned}`
$$

--
Three equivalent specifications

```r
m1a <- lmer(g5_spring ~ g4_spring + g3_spring + 
              (1|scid) + (1|distid),
            data = d)

m1b <- lmer(g5_spring ~ g4_spring + g3_spring + (1|distid/scid),
            data = d)

m1c <- lmer(g5_spring ~ g4_spring + g3_spring + 
              (1|distid) + (1|distid:scid),
            data = d)
```

---
# Compute starting group means

```r
d <- d %>% 
  group_by(scid) %>% 
  mutate(sch_mean_start = mean(g3_fall)) %>% 
  group_by(distid) %>% 
  mutate(dist_mean_start = mean(g3_fall))
```

---
# Model 2
Don't worry if you run into convergence warnings

$$
\small
`\begin{aligned}
  \operatorname{g5\_spring}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1}(\operatorname{g4\_spring}) + \beta_{2j[i]}(\operatorname{g3\_spring}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{2j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{sch\_mean\_start}) \\
      &\mu_{\beta_{2j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{2j}} \\ 
     \rho_{\beta_{2j}\alpha_{j}} & \sigma^2_{\beta_{2j}}
  \end{array}
\right)
 \right)
    \text{, for scid j = 1,} \dots \text{,J} \\    \alpha_{k}  &\sim N \left(\mu_{\alpha_{k}}, \sigma^2_{\alpha_{k}} \right)
    \text{, for distid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(g5_spring ~ g4_spring + g3_spring + sch_mean_start + 
       (g3_spring|scid) + (1|distid),
     data = d)
```

---
# Model 3

$$
\small
`\begin{aligned}
  \operatorname{g5\_spring}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{g4\_spring}) + \beta_{2j[i],k[i]}(\operatorname{g3\_spring}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j} \\
      &\beta_{2j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{sch\_mean\_start}) \\
      &\mu_{\beta_{1j}} \\
      &\mu_{\beta_{2j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} & \rho_{\alpha_{j}\beta_{2j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}} & \rho_{\beta_{1j}\beta_{2j}} \\ 
     \rho_{\beta_{2j}\alpha_{j}} & \rho_{\beta_{2j}\beta_{1j}} & \sigma^2_{\beta_{2j}}
  \end{array}
\right)
 \right)
    \text{, for scid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\beta_{2k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{k}} \\
      &\mu_{\beta_{1k}} \\
      &\mu_{\beta_{2k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} & \rho_{\alpha_{k}\beta_{2k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}} & \rho_{\beta_{1k}\beta_{2k}} \\ 
     \rho_{\beta_{2k}\alpha_{k}} & \rho_{\beta_{2k}\beta_{1k}} & \sigma^2_{\beta_{2k}}
  \end{array}
\right)
 \right)
    \text{, for distid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(g5_spring ~ g4_spring + g3_spring + sch_mean_start + 
       (g4_spring + g3_spring|scid) + 
       (g4_spring + g3_spring|distid),
     data = d)
```

---
# Model 4

$$
\small
`\begin{aligned}
  \operatorname{g5\_spring}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{g4\_spring}) + \beta_{2j[i],k[i]}(\operatorname{g3\_spring}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j} \\
      &\beta_{2j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{sch\_mean\_start}) \\
      &\mu_{\beta_{1j}} \\
      &\gamma^{\beta_{2}}_{0} + \gamma^{\beta_{2}}_{1}(\operatorname{sch\_mean\_start})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} & \rho_{\alpha_{j}\beta_{2j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}} & \rho_{\beta_{1j}\beta_{2j}} \\ 
     \rho_{\beta_{2j}\alpha_{j}} & \rho_{\beta_{2j}\beta_{1j}} & \sigma^2_{\beta_{2j}}
  \end{array}
\right)
 \right)
    \text{, for scid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\beta_{2k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{k}} \\
      &\mu_{\beta_{1k}} \\
      &\mu_{\beta_{2k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} & \rho_{\alpha_{k}\beta_{2k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}} & \rho_{\beta_{1k}\beta_{2k}} \\ 
     \rho_{\beta_{2k}\alpha_{k}} & \rho_{\beta_{2k}\beta_{1k}} & \sigma^2_{\beta_{2k}}
  \end{array}
\right)
 \right)
    \text{, for distid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(g5_spring ~ g4_spring + g3_spring + 
       sch_mean_start + sch_mean_start:g3_spring +
       (g4_spring + g3_spring|scid) + 
       (g4_spring + g3_spring|distid),
     data = d)
```

---
# Model 5
A little bit tricky

$$
\small
`\begin{aligned}
  \operatorname{g5\_spring}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{g4\_spring}) + \beta_{2j[i],k[i]}(\operatorname{g3\_spring}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j} \\
      &\beta_{2j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}} \\
      &\mu_{\beta_{2j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{j}} & 0 & 0 \\ 
     0 & \sigma^2_{\beta_{1j}} & 0 \\ 
     0 & 0 & \sigma^2_{\beta_{2j}}
  \end{array}
\right)
 \right)
    \text{, for scid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\beta_{2k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{dist\_mean\_start}) \\
      &\mu_{\beta_{1k}} \\
      &\mu_{\beta_{2k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{k}} & 0 & 0 \\ 
     0 & \sigma^2_{\beta_{1k}} & 0 \\ 
     0 & 0 & \sigma^2_{\beta_{2k}}
  \end{array}
\right)
 \right)
    \text{, for distid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(g5_spring ~ g4_spring + g3_spring + dist_mean_start +
       (g4_spring + g3_spring||scid) + 
       (g4_spring + g3_spring||distid),
     data = d)
```

---
# Move to long

```r
l <- d %>% 
  pivot_longer(
    cols = starts_with("g"),
    names_to = "timepoint",
    values_to = "score"
  )
l
```

```
## # A tibble: 202,500 x 7
## # Groups:   distid [100]
##    distid scid  sid   sch_mean_start dist_mean_start timepoint    score
##     <dbl> <chr> <chr>          <dbl>           <dbl> <chr>        <dbl>
##  1      1 1-1   1-1-1       195.1831        189.6743 g3_fall   203.0107
##  2      1 1-1   1-1-1       195.1831        189.6743 g3_winter 202.4761
##  3      1 1-1   1-1-1       195.1831        189.6743 g3_spring 212.2639
##  4      1 1-1   1-1-1       195.1831        189.6743 g4_fall   205.3442
##  5      1 1-1   1-1-1       195.1831        189.6743 g4_winter 214.2586
##  6      1 1-1   1-1-1       195.1831        189.6743 g4_spring 220.2867
##  7      1 1-1   1-1-1       195.1831        189.6743 g5_fall   220.5970
##  8      1 1-1   1-1-1       195.1831        189.6743 g5_winter 220.9811
##  9      1 1-1   1-1-1       195.1831        189.6743 g5_spring 237.0075
## 10      1 1-1   1-1-2       195.1831        189.6743 g3_fall   195.4607
## # … with 202,490 more rows
```

---
# Recode timepoint

First create a data frame that maps the existing values to the new values you want.

```r
wave_frame <- tibble(
  timepoint = paste0(
    "g", 
    rep(3:5, each = 3), 
    rep(c("_fall", "_winter", "_spring"), 3)
  ),
  wave = 0:8
)
wave_frame
```

```
## # A tibble: 9 x 2
##   timepoint  wave
##   <chr>     <int>
## 1 g3_fall       0
## 2 g3_winter     1
## 3 g3_spring     2
## 4 g4_fall       3
## 5 g4_winter     4
## 6 g4_spring     5
## 7 g5_fall       6
## 8 g5_winter     7
## 9 g5_spring     8
```

---
# Join

```r
l <- left_join(l, wave_frame)
```

```
## Joining, by = "timepoint"
```

```r
l
```

```
## # A tibble: 202,500 x 8
## # Groups:   distid [100]
##    distid scid  sid   sch_mean_start dist_mean_start timepoint    score  wave
##     <dbl> <chr> <chr>          <dbl>           <dbl> <chr>        <dbl> <int>
##  1      1 1-1   1-1-1       195.1831        189.6743 g3_fall   203.0107     0
##  2      1 1-1   1-1-1       195.1831        189.6743 g3_winter 202.4761     1
##  3      1 1-1   1-1-1       195.1831        189.6743 g3_spring 212.2639     2
##  4      1 1-1   1-1-1       195.1831        189.6743 g4_fall   205.3442     3
##  5      1 1-1   1-1-1       195.1831        189.6743 g4_winter 214.2586     4
##  6      1 1-1   1-1-1       195.1831        189.6743 g4_spring 220.2867     5
##  7      1 1-1   1-1-1       195.1831        189.6743 g5_fall   220.5970     6
##  8      1 1-1   1-1-1       195.1831        189.6743 g5_winter 220.9811     7
##  9      1 1-1   1-1-1       195.1831        189.6743 g5_spring 237.0075     8
## 10      1 1-1   1-1-2       195.1831        189.6743 g3_fall   195.4607     0
## # … with 202,490 more rows
```

---
# Model 6

$$
`\begin{aligned}
  \operatorname{score}_{i}  &\sim N \left(\alpha_{j[i],k[i],l[i]} + \beta_{1j[i],k[i]}(\operatorname{wave}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{k}} \\
      &\mu_{\beta_{1k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}}
  \end{array}
\right)
 \right)
    \text{, for scid k = 1,} \dots \text{,K} \\    \alpha_{l}  &\sim N \left(\mu_{\alpha_{l}}, \sigma^2_{\alpha_{l}} \right)
    \text{, for distid l = 1,} \dots \text{,L}
\end{aligned}`
$$

```r
lmer(score ~ wave +
       (wave|sid) + (wave|scid) + (1|distid),
     data = d)
```

---
# Model 7
This one takes a while to fit, so don't worry about actually fitting it, just try to write the code.

$$
\scriptsize
`\begin{aligned}
  \operatorname{score}_{i}  &\sim N \left(\alpha_{j[i],k[i],l[i]} + \beta_{1j[i],k[i]}(\operatorname{wave}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\mu_{\alpha_{j}} \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1l[i]}^{\alpha}(\operatorname{sch\_mean\_start}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{sch\_mean\_start})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}}
  \end{array}
\right)
 \right)
    \text{, for scid k = 1,} \dots \text{,K} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{l} \\
      &\gamma_{1l}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{dist\_mean\_start}) + \gamma_{2}^{\alpha}(\operatorname{dist\_mean\_start} \times \operatorname{wave}) \\
      &\mu_{\gamma_{1l}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{l}} & \rho_{\alpha_{l}\gamma_{1l}} \\ 
     \rho_{\gamma_{1l}\alpha_{l}} & \sigma^2_{\gamma_{1l}}
  \end{array}
\right)
 \right)
    \text{, for distid l = 1,} \dots \text{,L}
\end{aligned}`
$$

```r
lmer(score ~ wave + sch_mean_start + dist_mean_start +
       wave:sch_mean_start + wave:dist_mean_start +
       (wave|sid) + (wave|scid) + (sch_mean_start|distid),
     data = l)
```

---
# Model 8

## Last one

$$
\scriptsize
`\begin{aligned}
  \operatorname{score}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{wave}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{sch\_mean\_start}) + \gamma_{2}^{\alpha}(\operatorname{dist\_mean\_start}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{sch\_mean\_start})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(score ~ wave * sch_mean_start + dist_mean_start +
       (wave|sid),
     data = l)
```

---
class: inverse-blue middle
# Growth modeling

---
# The data
### Sample of the Children of the National Longitudinal Study of Youth

--
Outcome = `piat` = Peabody Individual Achievement Test

--
Please read in `cnlsy.csv` now

```r
library(tidyverse)
d <- read_csv(here::here("data", "cnlsy.csv"))
```

---
# Look at the data

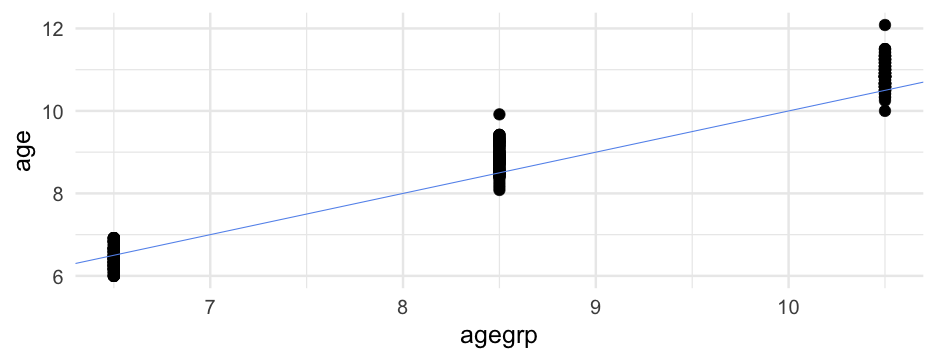
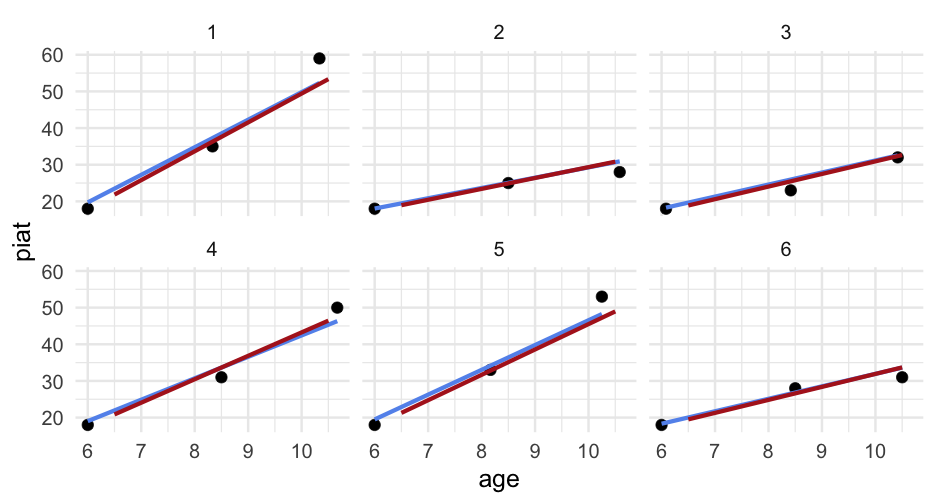
```r
d
```

```
## # A tibble: 267 x 5
##       id  wave agegrp       age  piat
##    <dbl> <dbl>  <dbl>     <dbl> <dbl>
##  1     1     1    6.5  6           18
##  2     1     2    8.5  8.333333    35
##  3     1     3   10.5 10.33333     59
##  4     2     1    6.5  6           18
##  5     2     2    8.5  8.5         25
##  6     2     3   10.5 10.58333     28
##  7     3     1    6.5  6.083333    18
##  8     3     2    8.5  8.416667    23
##  9     3     3   10.5 10.41667     32
## 10     4     1    6.5  6           18
## # … with 257 more rows
```

---
# Fit a basic model
Please try to fit a model that accounts for the within-subjects design in some way and includes a random intercept and slope.

```r
library(lme4)
d <- d %>% 
  mutate(wave_c = wave - 1)
m_wave <- lmer(piat ~ wave_c + (wave_c|id),
               data = d)
```

---
# Interpret

```r
arm::display(m_wave)
```

```
## lmer(formula = piat ~ wave_c + (wave_c | id), data = d)
##             coef.est coef.se
## (Intercept) 21.16     0.62  
## wave_c      10.06     0.59  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr 
##  id       (Intercept) 3.38          
##           wave_c      4.24     0.22 
##  Residual             5.20          
## ---
## number of obs: 267, groups: id, 89
## AIC = 1830.4, DIC = 1821.5
## deviance = 1819.9
```

--
But what does a one unit increase in `wave_c` actually mean?

---
# More meaningful
* Note that each `wave` is tied to a specific age group (the approximate age of participants at that age). Can we use this? Try!

```r
m_agegrp <- lmer(piat ~ agegrp + (agegrp|id),
                 data = d,
                 control = lmerControl(optimizer = "bobyqa"))
```

---
# Interpret
What does the intercept mean here? Age group?

```r
arm::display(m_agegrp)
```

```
## lmer(formula = piat ~ agegrp + (agegrp | id), data = d, control = lmerControl(optimizer = "bobyqa"))
##             coef.est coef.se
## (Intercept) -11.54     2.21 
## agegrp        5.03     0.30 
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  id       (Intercept) 13.43          
##           agegrp       2.12    -0.97 
##  Residual              5.20          
## ---
## number of obs: 267, groups: id, 89
## AIC = 1831.8, DIC = 1820.1
## deviance = 1819.9
```

---
# How do we fix the intercept?

--
## Centering
Let's center age group on the first time point

```r
d <- d %>% 
  mutate(agegrp_c = agegrp - 6.5)
m_agegrp2 <- lmer(piat ~ agegrp_c + (agegrp_c|id),
                 data = d,
                 control = lmerControl(optimizer = "bobyqa"))
```

---
# Interpret
What does the intercept represent now?

```r
arm::display(m_agegrp2)
```

```
## lmer(formula = piat ~ agegrp_c + (agegrp_c | id), data = d, control = lmerControl(optimizer = "bobyqa"))
##             coef.est coef.se
## (Intercept) 21.16     0.62  
## agegrp_c     5.03     0.30  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr 
##  id       (Intercept) 3.38          
##           agegrp_c    2.12     0.22 
##  Residual             5.20          
## ---
## number of obs: 267, groups: id, 89
## AIC = 1831.8, DIC = 1820.1
## deviance = 1819.9
```

--
Pop Quiz: Without looking, how do you think the fit of the model has changed?

---
# Comparing fit

```r
library(performance)
compare_performance(m_agegrp, m_agegrp2) %>% 
  print_md()
```

Table: Comparison of Model Performance Indices

|Name      |   Model |     AIC |     BIC | R2 (cond.) | R2 (marg.) |  ICC | RMSE | Sigma |
|:---------|:-------:|:-------:|:-------:|:----------:|:----------:|:----:|:----:|:-----:|
|m_agegrp  | lmerMod | 1831.78 | 1853.30 |       0.81 |       0.48 | 0.64 | 4.15 |  5.20 |
|m_agegrp2 | lmerMod | 1831.78 | 1853.30 |       0.81 |       0.48 | 0.64 | 4.15 |  5.20 |

They're identical!

---
# Slightly different
Compare model predictions

![](w6p1_files/figure-html/unnamed-chunk-32-1.png)

---
# Age

* Notice that `agegrp` does not always correspond directly with their *actual* age.

```r
ggplot(d, aes(agegrp, age)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1,
              color = "cornflowerblue")
```

![](w6p1_files/figure-html/unnamed-chunk-33-1.png)

---
# Model assumptions
* When we use the `agegrp` variable, we are assuming that all children are *the exact same age* at each assessment wave.

* Although `agegrp` is more interpretable than `wave`, it doesn't solve all our problems

--
.center[.realbig[You try]]

Fit another model with `age` as the time variable instead. How do the results compare?

---
# Intercept

How do we want to handle this? Probably need to do something.

--
Look at first time point

```r
d %>% 
  filter(wave == 1) %>% 
  count(age)
```

```
## # A tibble: 12 x 2
##         age     n
##       <dbl> <int>
##  1 6            6
##  2 6.083333     4
##  3 6.166667     9
##  4 6.25         9
##  5 6.333333    10
##  6 6.416667    11
##  7 6.5          7
##  8 6.583333     7
##  9 6.666667     9
## 10 6.75         3
## 11 6.833333     7
## 12 6.916667     7
```

---
# Centering
* I'll choose to subtract 6 from each age

* what will this value represent for students who were 6.91 years old at the first wave?

--
  + Backwards projection
  
--

```r
d <- d %>% 
  mutate(age6 = age - 6)

m_age <- lmer(piat ~ age6 + (age6|id), data = d)
```

---
# Summary

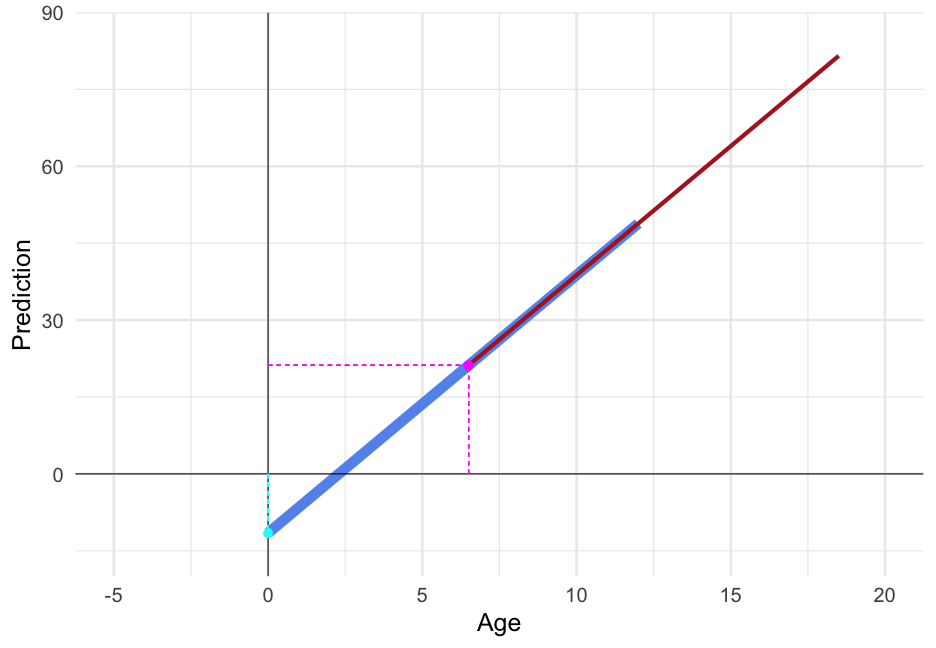
```r
arm::display(m_age)
```

```
## lmer(formula = piat ~ age6 + (age6 | id), data = d)
##             coef.est coef.se
## (Intercept) 18.79     0.61  
## age6         4.54     0.26  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr 
##  id       (Intercept) 2.01          
##           age6        1.84     0.17 
##  Residual             5.23          
## ---
## number of obs: 267, groups: id, 89
## AIC = 1816.1, DIC = 1803.6
## deviance = 1803.9
```

---
# Compare fit

```r
compare_performance(m_wave, m_agegrp2, m_age) %>% 
  print_md()
```

Table: Comparison of Model Performance Indices

|Name      |   Model |     AIC |     BIC | R2 (cond.) | R2 (marg.) |  ICC | RMSE | Sigma |
|:---------|:-------:|:-------:|:-------:|:----------:|:----------:|:----:|:----:|:-----:|
|m_wave    | lmerMod | 1830.39 | 1851.92 |       0.81 |       0.48 | 0.64 | 4.15 |  5.20 |
|m_agegrp2 | lmerMod | 1831.78 | 1853.30 |       0.81 |       0.48 | 0.64 | 4.15 |  5.20 |
|m_age     | lmerMod | 1816.14 | 1837.67 |       0.81 |       0.50 | 0.62 | 4.34 |  5.23 |

---
# Difference in predictions

```r
pred_frame <- d %>% 
  mutate(pred_agegrp = predict(m_agegrp2),
         pred_age = predict(m_age)) %>% 
  filter(id %in% 1:6)
```

---

```r
ggplot(pred_frame, aes(age, piat)) +
  geom_point() +
  geom_line(aes(x = age6 + 6, y = pred_age),
            color = "cornflowerblue") +
  geom_line(aes(x = agegrp_c + 6.5, y = pred_agegrp),
            color = "firebrick") +
  facet_wrap(~id)
```

![](w6p1_files/figure-html/unnamed-chunk-39-1.png)

---
class: inverse-orange middle
# Differences
The differences in the model predictions overall appear modest, but it does display better fit to the data, and the assumptions we're making are less stringent.

---
# Changing interpretation

* In this case, our coefficient for age is interepeted in years.

--
> On average, children gained 4.54 points on the Peabody Individual Achievement Test **per year**.

--
### Challenge
Can you change the model so the coefficient represents monthly growth?

---
# Solution
Just  multiply `age` by 12 to get it coded in months.

```r
d <- d %>% 
  mutate(age_months = age6 * 12)
d
```

```
## # A tibble: 267 x 9
##       id  wave agegrp       age  piat wave_c agegrp_c       age6 age_months
##    <dbl> <dbl>  <dbl>     <dbl> <dbl>  <dbl>    <dbl>      <dbl>      <dbl>
##  1     1     1    6.5  6           18      0        0 0            0       
##  2     1     2    8.5  8.333333    35      1        2 2.333333    28       
##  3     1     3   10.5 10.33333     59      2        4 4.333333    52       
##  4     2     1    6.5  6           18      0        0 0            0       
##  5     2     2    8.5  8.5         25      1        2 2.5         30       
##  6     2     3   10.5 10.58333     28      2        4 4.583333    55       
##  7     3     1    6.5  6.083333    18      0        0 0.08333333   1.000000
##  8     3     2    8.5  8.416667    23      1        2 2.416667    29       
##  9     3     3   10.5 10.41667     32      2        4 4.416667    53       
## 10     4     1    6.5  6           18      0        0 0            0       
## # … with 257 more rows
```

---
# Refit

```r
m_months <- lmer(piat ~ age_months + (age_months|id), data = d,
                 control = lmerControl(optimizer = "bobyqa"))
arm::display(m_months)
```

```
## lmer(formula = piat ~ age_months + (age_months | id), data = d, 
##     control = lmerControl(optimizer = "bobyqa"))
##             coef.est coef.se
## (Intercept) 18.79     0.61  
## age_months   0.38     0.02  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr 
##  id       (Intercept) 2.01          
##           age_months  0.15     0.17 
##  Residual             5.23          
## ---
## number of obs: 267, groups: id, 89
## AIC = 1821.1, DIC = 1798.7
## deviance = 1803.9
```

---
# Which model fits better?
Before we test - what do you suspect?

--
## They are not actually the same

```r
compare_performance(m_age, m_months)
```

```
## # Comparison of Model Performance Indices
## 
## Name     |   Model |      AIC |      BIC | R2 (cond.) | R2 (marg.) |   ICC |  RMSE | Sigma
## ------------------------------------------------------------------------------------------
## m_age    | lmerMod | 1816.145 | 1837.668 |      0.807 |      0.496 | 0.618 | 4.341 | 5.235
## m_months | lmerMod | 1821.115 | 1842.638 |      0.807 |      0.496 | 0.618 | 4.341 | 5.235
```

---
# But they are essentially

```r
pred_frame %>% 
  mutate(pred_months = predict(m_months)[1:18]) %>% 
  select(id, starts_with("pred"))
```

```
## # A tibble: 18 x 4
##       id pred_agegrp pred_age pred_months
##    <dbl>       <dbl>    <dbl>       <dbl>
##  1     1    21.85047 19.72314    19.72322
##  2     1    37.59817 37.27018    37.27026
##  3     1    53.34587 52.31049    52.31057
##  4     2    18.95405 18.04288    18.04279
##  5     2    24.89376 25.06252    25.06245
##  6     2    30.83348 30.91222    30.91217
##  7     3    18.88021 18.29429    18.29419
##  8     3    25.75976 25.95783    25.95776
##  9     3    32.63931 32.52659    32.52655
## 10     4    20.86038 19.03189    19.03190
## 11     4    33.65203 33.64630    33.64632
## 12     4    46.44368 46.31212    46.31215
## 13     5    21.28110 19.49879    19.49885
## 14     5    35.12409 34.15691    34.15697
## 15     5    48.96708 48.25126    48.25132
## 16     6    19.51079 18.32752    18.32747
## 17     6    26.60084 26.82974    26.82970
## 18     6    33.69089 33.63151    33.63148
```

---
class: inverse-blue middle
# Another example
With more complications

---
# Wages data
Please read in the `wages.csv` dataset.

```r
wages <- read_csv(here::here("data", "wages.csv"))
```

```
## 
## ── Column specification ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
## cols(
##   id = col_double(),
##   lnw = col_double(),
##   exper = col_double(),
##   ged = col_double(),
##   black = col_double(),
##   hispanic = col_double(),
##   hgc = col_double(),
##   uerate = col_double()
## )
```

---
# Data
* Mournane, Boudett, and Willett (1999)
* National Longitudinal Survey of Youth
* Studied wages of individuals who dropped out of high school

### Variables
* `id`: Participant ID
* `lnw`: Natural log of wages
* `exper`: Experience, in years
* `ged`: Whether or not they completed a GED
* `black`, `hispanic`: Dummy variables for race/ethnicity
* `hgc`: Highest grade completed
* `uerate`: Unemployment rate at the time

---
# Complications

```r
wages %>% 
  filter(id %in% c(206, 332))
```

```
## # A tibble: 13 x 8
##       id   lnw exper   ged black hispanic   hgc uerate
##    <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl> <dbl>  <dbl>
##  1   206 2.028 1.874     0     0        0    10  9.2  
##  2   206 2.297 2.814     0     0        0    10 11    
##  3   206 2.482 4.314     0     0        0    10  6.295
##  4   332 1.63  0.125     0     0        1     8  7.1  
##  5   332 1.476 1.625     0     0        1     8  9.6  
##  6   332 1.804 2.413     0     0        1     8  7.2  
##  7   332 1.439 3.393     0     0        1     8  6.195
##  8   332 1.748 4.47      0     0        1     8  5.595
##  9   332 1.526 5.178     0     0        1     8  4.595
## 10   332 2.044 6.082     0     0        1     8  4.295
## 11   332 2.179 7.043     0     0        1     8  3.395
## 12   332 2.186 8.197     0     0        1     8  4.395
## 13   332 4.035 9.092     0     0        1     8  6.695
```

---
# Complications
* Unbalanced data

```r
wages %>% 
  count(id) %>% 
  summarize(range = range(n))
```

```
## # A tibble: 2 x 1
##   range
##   <int>
## 1     1
## 2    13
```

* Participants age ranged from 14-17 at first time point

* Unequal spacing between waves

---
# Complications

* Participants dropped out at different times, entered the workforce and different times, and switched jobs at different times

* A decision was made to clock *time* from their first day of work

* The `exper` variable tracks their overall time in the workforce, and time at a given salary

---
# Fitting a model
* The hard part - structuring the data - is already done. We really don't have to do anything special here to account for all these complexities!

```r
m_wage0 <- lmer(lnw ~ exper + (exper|id), data = wages,
                control = lmerControl(optimizer = "bobyqa"))
```

---

```r
arm::display(m_wage0)
```

```
## lmer(formula = lnw ~ exper + (exper | id), data = wages, control = lmerControl(optimizer = "bobyqa"))
##             coef.est coef.se
## (Intercept) 1.72     0.01   
## exper       0.05     0.00   
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  id       (Intercept) 0.23           
##           exper       0.04     -0.30 
##  Residual             0.31           
## ---
## number of obs: 6402, groups: id, 888
## AIC = 4951.3, DIC = 4903.5
## deviance = 4921.4
```

--
Every one year of extra experience corresponded to a 0.05 increase in log wages, on average, which varied across participants with a standard deviation of 0.04.

---
# Challenge
Let's fit a more interesting model. Try to fit a model that addresses the following questions:

> Is the relation between experience and log wages the same across coded race/ethnicity categories? 
Do these relations depend on highest grade completed?

---
# Centering
Let's center highest grade completed. You could choose whatever value makes the most sense to you. I'll choose Grade 9.

```r
wages <- wages %>% 
  mutate(hgc_9 = hgc - 9)
```

---
# Is this right?
If not, what is it missing?

```r
m_wage1 <- lmer(lnw ~ exper + black + hispanic + hgc_9 +
                  (exper|id),
                data = wages,
                control = lmerControl(optimizer = "bobyqa"))
```

---
# Random effects
In the previous model, I specified `exper` as randomly varying across `id` levels.

--
Could or should I have set any of the other variables to vary randomly? Why or why not?

---
# Marginal predictions

```r
pred_frame <- expand.grid(
  exper = 0:15,
  black = 0:1,
  hispanic = 0:1,
  hgc_9 = 6:12 - 9,
  id = -999
)

pred_frame <- pred_frame %>% 
  mutate(pred = predict(m_wage1, 
                        pred_frame, 
                        allow.new.levels = TRUE))
```

---
# Race/Ethnicity
Let's create a new variable that has all the race/ethnicity *labels* instead of the dummy codes.

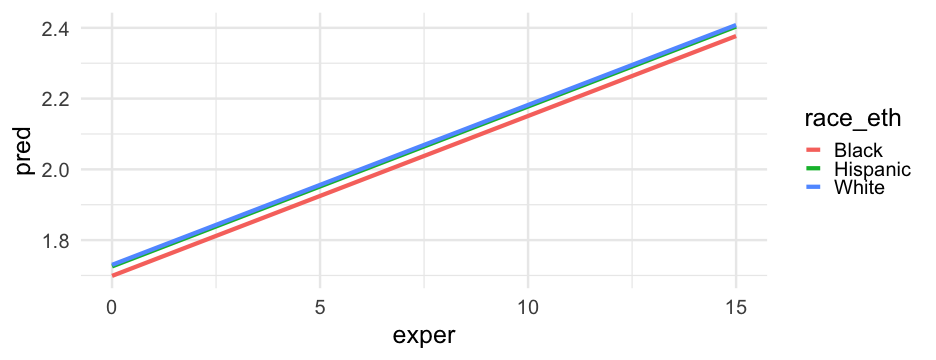
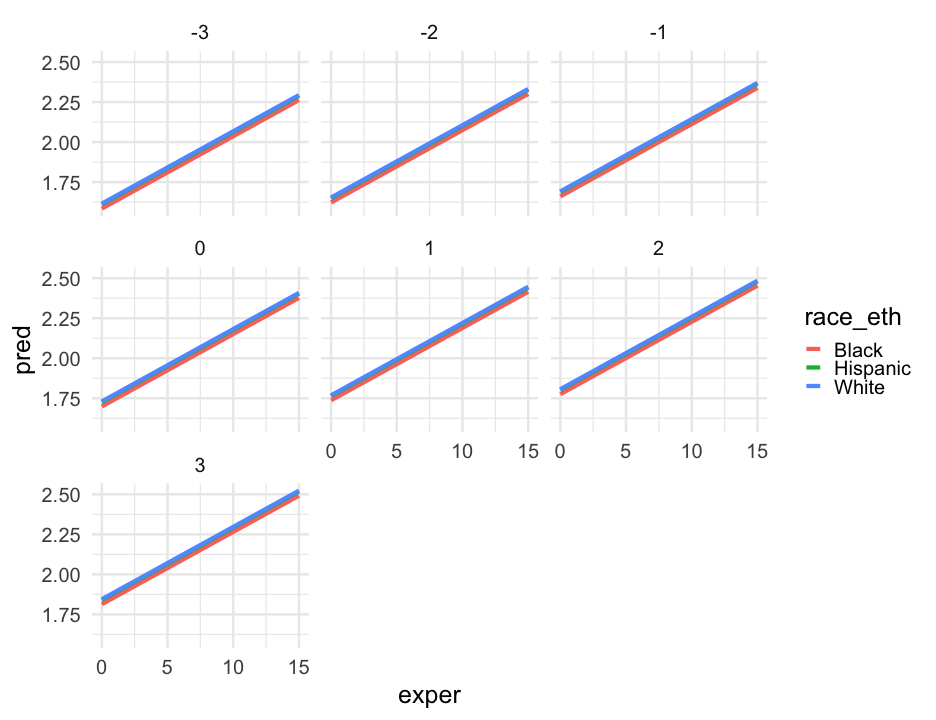
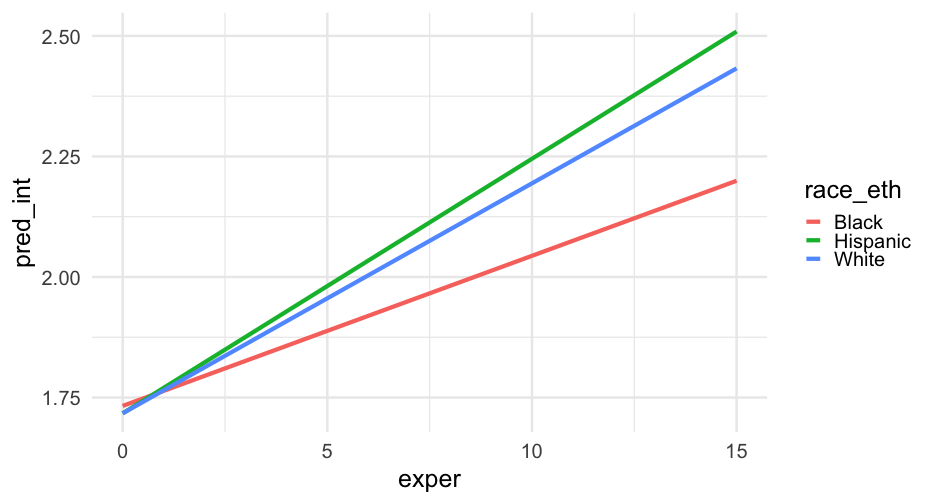
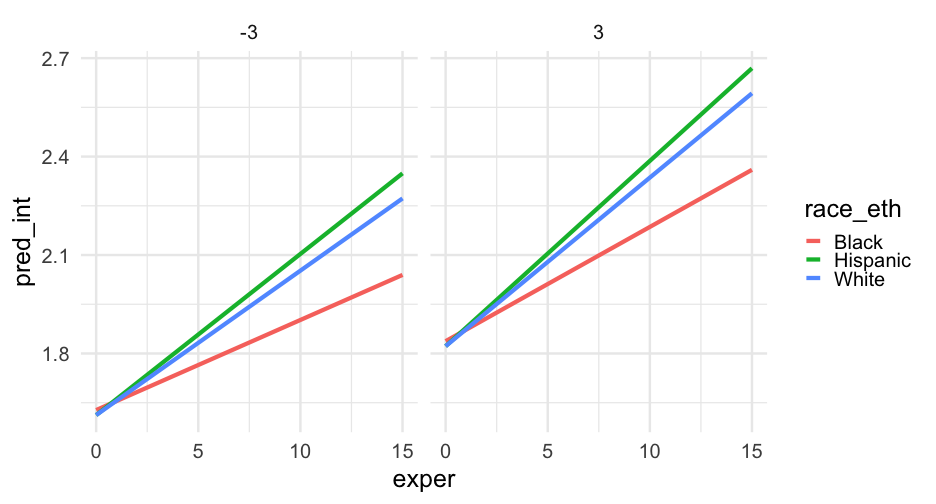
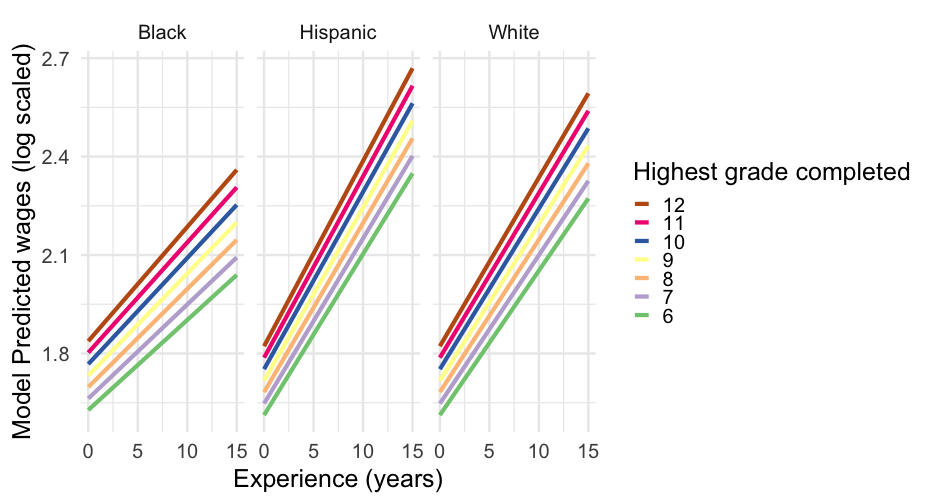
```r
pred_frame <- pred_frame %>% 
  mutate(
    race_eth = case_when(
      black == 0 & hispanic == 0 ~ "White",
      black == 1 & hispanic == 0 ~ "Black",
      black == 0 & hispanic == 1 ~ "Hispanic",
      TRUE ~ NA_character_
    )
  )
```

---
# Plots
Look at just `hgc_9 == 0`.

```r
pred_frame %>% 
  drop_na() %>% 
  filter(hgc_9 == 0) %>% 
  ggplot(aes(exper, pred)) +
  geom_line(aes(color = race_eth)) 
```

![](w6p1_files/figure-html/unnamed-chunk-53-1.png)

---
# All hgc
![](w6p1_files/figure-html/unnamed-chunk-54-1.png)

---
# Interactions
If we want to know how the *slope* may or may not depend on these variables, we have to model the interactions.

--
## Just the two-way interactions

```r
m_wage2 <- lmer(lnw ~ exper + black + exper:black +
                  exper:hispanic + 
                  hgc_9 + exper:hgc_9 +
                  (exper|id),
                data = wages,
                control = lmerControl(optimizer = "bobyqa"))
```

---
# Reproduce the plots
### First make new predictions

```r
pred_frame <- pred_frame %>% 
  mutate(pred_int = predict(m_wage2, 
                            newdata = pred_frame, 
                            allow.new.levels = TRUE))
```

---
# Plot

```r
pred_frame %>% 
  drop_na() %>% 
  filter(hgc_9 == 0) %>% 
  ggplot(aes(exper, pred_int)) +
  geom_line(aes(color = race_eth)) 
```

![](w6p1_files/figure-html/unnamed-chunk-57-1.png)

---

```r
pred_frame %>% 
  drop_na() %>% 
  filter(hgc_9 == -3 | hgc_9 == 3) %>% 
  ggplot(aes(exper, pred_int)) +
  geom_line(aes(color = race_eth)) +
  facet_wrap(~hgc_9)
```

![](w6p1_files/figure-html/unnamed-chunk-58-1.png)

---
# Focus on hgc

```r
pred_frame %>% 
  drop_na() %>% 
  ggplot(aes(exper, pred_int)) +
  geom_line(aes(color = factor(hgc_9))) +
  facet_wrap(~race_eth) +
  scale_color_brewer("Highest grade completed", 
                     palette = "Accent", 
                     breaks = 3:-3,
                     labels = 12:6) +
  labs(x = "Experience (years)",
       y = "Model Predicted wages (log scaled)")
```

---
class: full-slide-fig middle

![](w6p1_files/figure-html/unnamed-chunk-60-1.png)

---
# Coefficient interpretation
Notice I started with the plots

* In *presenting* a model, this is generally what I would do

- I think this generally helps interpretation
  
* In practice I generally start by looking at the coefficients

---
# Model summary

```r
arm::display(m_wage2)
```

```
## lmer(formula = lnw ~ exper + black + exper:black + exper:hispanic + 
##     hgc_9 + exper:hgc_9 + (exper | id), data = wages, control = lmerControl(optimizer = "bobyqa"))
##                coef.est coef.se
## (Intercept)     1.72     0.01  
## exper           0.05     0.00  
## black           0.02     0.02  
## hgc_9           0.03     0.01  
## exper:black    -0.02     0.01  
## exper:hispanic  0.01     0.00  
## exper:hgc_9     0.00     0.00  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  id       (Intercept) 0.23           
##           exper       0.04     -0.31 
##  Residual             0.31           
## ---
## number of obs: 6402, groups: id, 888
## AIC = 4955.1, DIC = 4811.9
## deviance = 4872.5
```

---
class: inverse-blue middle
# Handling non-linearity

---
# The data
Simulated data to mimic a common form of non-linearity.

Notice the "true" intercept and slope for each student is actually in the data.

```r
sim_d <- read_csv(here::here("data", "curvilinear-sim.csv"))
sim_d
```

```
## # A tibble: 2,760 x 5
##      sid      int    slope date           score
##    <dbl>    <dbl>    <dbl> <date>         <dbl>
##  1     1 31.91237 32.25614 2019-04-26 116.1638 
##  2     1 31.91237 32.25614 2019-04-14  50.02688
##  3     1 31.91237 32.25614 2019-05-21 151.8375 
##  4     2 22.91502 24.05294 2019-04-25  81.93698
##  5     2 22.91502 24.05294 2019-04-30  93.47374
##  6     2 22.91502 24.05294 2019-05-24 113.8067 
##  7     2 22.91502 24.05294 2019-04-27  87.83396
##  8     2 22.91502 24.05294 2019-05-29 112.8697 
##  9     2 22.91502 24.05294 2019-04-25  82.40156
## 10     2 22.91502 24.05294 2019-05-27 111.8477 
## # … with 2,750 more rows
```

---
# Complexities
Notice these data do have some complexities

--
Unbalance

```r
sim_d %>% 
  count(sid) %>% 
  summarize(range(n))
```

```
## # A tibble: 2 x 1
##   `range(n)`
##        <int>
## 1          3
## 2          8
```

---
# Varied "starting" points

```r
sim_d %>% 
  arrange(sid, date) %>% 
  group_by(sid) %>% 
  slice(1) %>% 
  ungroup() %>% 
  summarize(range(date))
```

```
## # A tibble: 2 x 1
##   `range(date)`
##   <date>       
## 1 2019-04-14   
## 2 2019-05-29
```

Overall date range

```r
range(sim_d$date)
```

```
## [1] "2019-04-14" "2019-06-08"
```

---
# Plot
Show the overall relation between `date` and `score`. What do you notice?

---

```r
ggplot(sim_d, aes(date, score)) +
  geom_point(alpha = 0.15, stroke = NA) +
  geom_smooth(se = FALSE, color = "#33B1AE", size = 2)
```

![](w6p1_files/figure-html/unnamed-chunk-66-1.png)

Ideas on how to model this?

---

```r
ggplot(sim_d, aes(date, score)) +
  geom_point(alpha = 0.15, stroke = NA) +
  geom_smooth(se = FALSE, color = "#33B1AE", size = 2) +
  geom_smooth(se = FALSE, method = "lm", color = "#808AFF", size = 2)
```

![](w6p1_files/figure-html/unnamed-chunk-67-1.png)

Linear modeling is not going to work...

---
# Polynomials

![](w6p1_files/figure-html/unnamed-chunk-68-1.png)

---
# Fit a model
Let's try fitting a linear model and a quadratic model and see which fits better.

--
You try fitting the linear model first, with `date` predicting `score`, and both the intercept and slope varying across students.

---
# Center date

Let's first center date and put it in interpretable units.

I'll center it on the first time point.

--
First - what do dates look like when converted to numbers?

```r
library(lubridate)
as_date(0)
```

```
## [1] "1970-01-01"
```

```r
as_date(1)
```

```
## [1] "1970-01-02"
```

One unit = one day.

---
# Center

```r
sim_d <- sim_d %>% 
  mutate(
    days_from_start = as.numeric(date) - min(as.numeric(date))
  )
```

---
# Fit linear model

```r
linear <- lmer(score ~ days_from_start + (days_from_start|sid), 
               data = sim_d,
               control = lmerControl(optimizer = "Nelder_Mead"))
arm::display(linear)
```

```
## lmer(formula = score ~ days_from_start + (days_from_start | sid), 
##     data = sim_d, control = lmerControl(optimizer = "Nelder_Mead"))
##                 coef.est coef.se
## (Intercept)     68.66     0.71  
## days_from_start  1.22     0.02  
## 
## Error terms:
##  Groups   Name            Std.Dev. Corr  
##  sid      (Intercept)     13.69          
##           days_from_start  0.28    -0.41 
##  Residual                  7.91          
## ---
## number of obs: 2760, groups: sid, 500
## AIC = 21005, DIC = 20981.9
## deviance = 20987.4
```

---
# Fit quadratic model

```r
sim_d <- sim_d %>% 
  mutate(days2 = days_from_start^2)

quad <- lmer(score ~ days_from_start + days2 + 
               (days_from_start|sid), 
             data = sim_d,
             control = lmerControl(optimizer = "Nelder_Mead"))
```

---
# Quadratic summary

```r
arm::display(quad)
```

```
## lmer(formula = score ~ days_from_start + days2 + (days_from_start | 
##     sid), data = sim_d, control = lmerControl(optimizer = "Nelder_Mead"))
##                 coef.est coef.se
## (Intercept)     52.09     0.54  
## days_from_start  2.98     0.03  
## days2           -0.03     0.00  
## 
## Error terms:
##  Groups   Name            Std.Dev. Corr 
##  sid      (Intercept)     10.07         
##           days_from_start  0.18    0.31 
##  Residual                  4.41         
## ---
## number of obs: 2760, groups: sid, 500
## AIC = 18279.8, DIC = 18224.7
## deviance = 18245.2
```

---
# Compare

```r
anova(linear, quad)
```

```
## refitting model(s) with ML (instead of REML)
```

```
## Data: sim_d
## Models:
## linear: score ~ days_from_start + (days_from_start | sid)
## quad: score ~ days_from_start + days2 + (days_from_start | sid)
##        npar   AIC   BIC   logLik deviance  Chisq Df Pr(>Chisq)    
## linear    6 20999 21035 -10493.7    20987                         
## quad      7 18259 18301  -9122.6    18245 2742.2  1  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
# Plot predictions

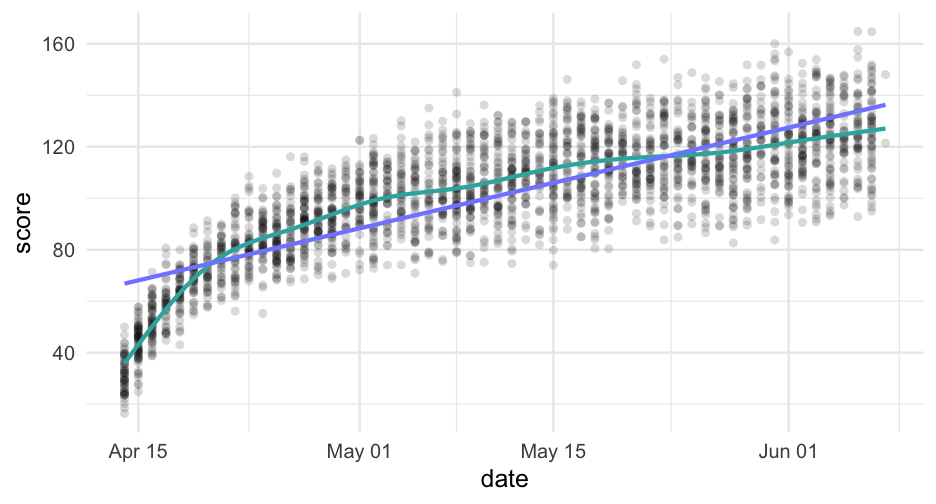
```r
pred_frame <- tibble(
    days_from_start = 0:max(sim_d$days_from_start),
    days2 = days_from_start^2,
    sid = -999
  ) %>% 
  mutate(pred_linear = predict(linear, 
                               newdata = ., 
                               allow.new.levels = TRUE),
         pred_quad = predict(quad, 
                             newdata = ., 
                             allow.new.levels = TRUE))
pred_frame
```

```
## # A tibble: 56 x 5
##    days_from_start days2   sid pred_linear pred_quad
##              <int> <dbl> <dbl>       <dbl>     <dbl>
##  1               0     0  -999    68.65771  52.09304
##  2               1     1  -999    69.87886  55.04428
##  3               2     4  -999    71.10000  57.93071
##  4               3     9  -999    72.32114  60.75233
##  5               4    16  -999    73.54228  63.50914
##  6               5    25  -999    74.76342  66.20114
##  7               6    36  -999    75.98456  68.82834
##  8               7    49  -999    77.20570  71.39072
##  9               8    64  -999    78.42684  73.88829
## 10               9    81  -999    79.64798  76.32105
## # … with 46 more rows
```

---

```r
ggplot(pred_frame, aes(days_from_start)) +
  geom_point(aes(y = score), data = sim_d, color = "gray80") +
  geom_line(aes(y = pred_linear), color = "#33B1AE") +
  geom_line(aes(y = pred_quad), color = "#808AFF")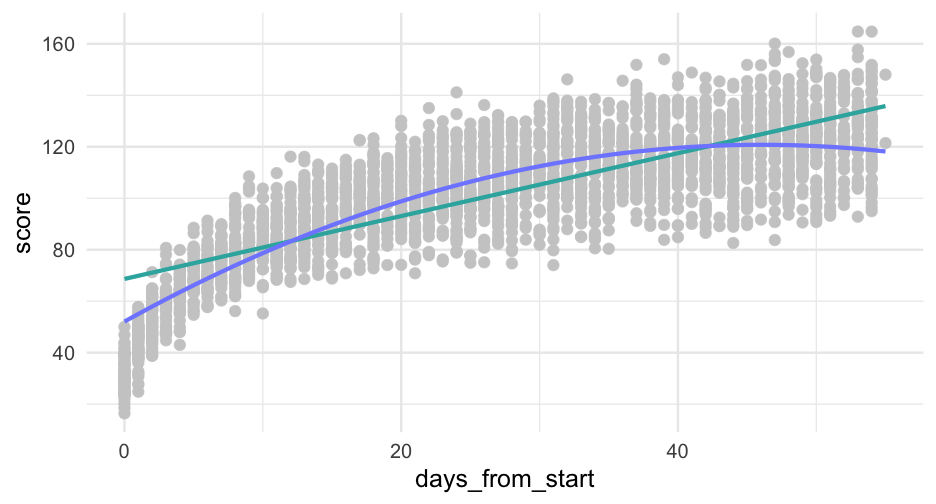
```

![](w6p1_files/figure-html/unnamed-chunk-76-1.png)

This is definitely looking better, but it's too high in the lower tail and maybe a bit too low in the upper

---
# Cubic?

You try first - extend what we just did to model a cubic trend

```r
sim_d <- sim_d %>% 
  mutate(days3 = days_from_start^3)

cubic <- lmer(score ~ days_from_start + days2 + days3 +
                (days_from_start|sid), 
             data = sim_d,
             control = lmerControl(optimizer = "Nelder_Mead"))
```

```
## Warning: Some predictor variables are on very different scales: consider rescaling
```

---
# Cubic summary

```r
arm::display(cubic)
```

```
## lmer(formula = score ~ days_from_start + days2 + days3 + (days_from_start | 
##     sid), data = sim_d, control = lmerControl(optimizer = "Nelder_Mead"))
##                 coef.est coef.se
## (Intercept)     43.64     0.49  
## days_from_start  4.93     0.04  
## days2           -0.12     0.00  
## days3            0.00     0.00  
## 
## Error terms:
##  Groups   Name            Std.Dev. Corr 
##  sid      (Intercept)     9.48          
##           days_from_start 0.15     0.55 
##  Residual                 2.81          
## ---
## number of obs: 2760, groups: sid, 500
## AIC = 16311.2, DIC = 16211.2
## deviance = 16253.2
```

---
# Compare

```r
anova(linear, quad, cubic)
```

```
## refitting model(s) with ML (instead of REML)
```

```
## Data: sim_d
## Models:
## linear: score ~ days_from_start + (days_from_start | sid)
## quad: score ~ days_from_start + days2 + (days_from_start | sid)
## cubic: score ~ days_from_start + days2 + days3 + (days_from_start | 
## cubic:     sid)
##        npar   AIC   BIC   logLik deviance  Chisq Df Pr(>Chisq)    
## linear    6 20999 21035 -10493.7    20987                         
## quad      7 18259 18301  -9122.6    18245 2742.2  1  < 2.2e-16 ***
## cubic     8 16269 16317  -8126.6    16253 1992.0  1  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
# Predictions

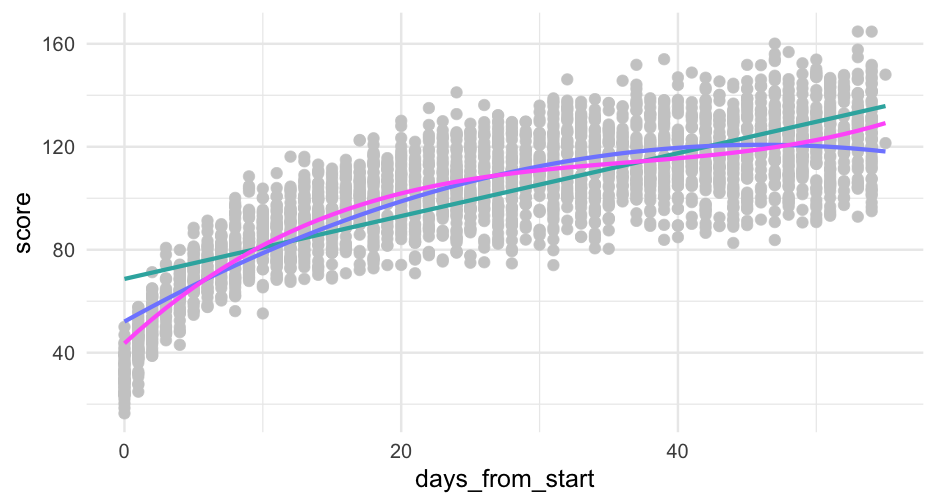
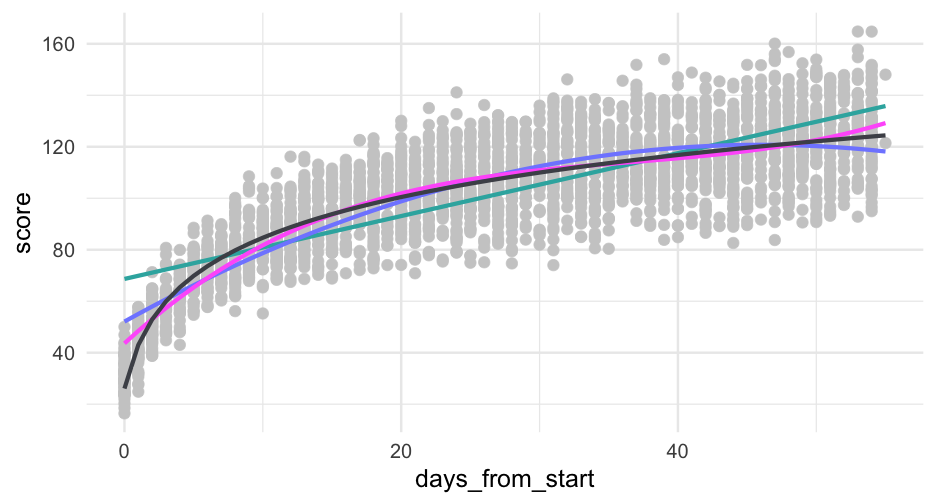
```r
pred_frame <- pred_frame %>% 
  mutate(days3 = days_from_start^3)

pred_frame %>% 
  mutate(pred_cubic = predict(cubic, 
                              newdata = ., 
                              allow.new.levels = TRUE)) %>% 
  ggplot(aes(days_from_start)) +
  geom_point(aes(y = score), data = sim_d, color = "gray80") +
  geom_line(aes(y = pred_linear), color = "#33B1AE") +
  geom_line(aes(y = pred_quad), color = "#808AFF") +
  geom_line(aes(y = pred_cubic), color = "#ff66fa")
```

---
class: middle

![](w6p1_files/figure-html/unnamed-chunk-81-1.png)

---
# Alternative
Instead of modeling additional parameters, just transform the data

--
## Common transformations

* log
* square root
* inverse `$1/x$`

---
# Try log
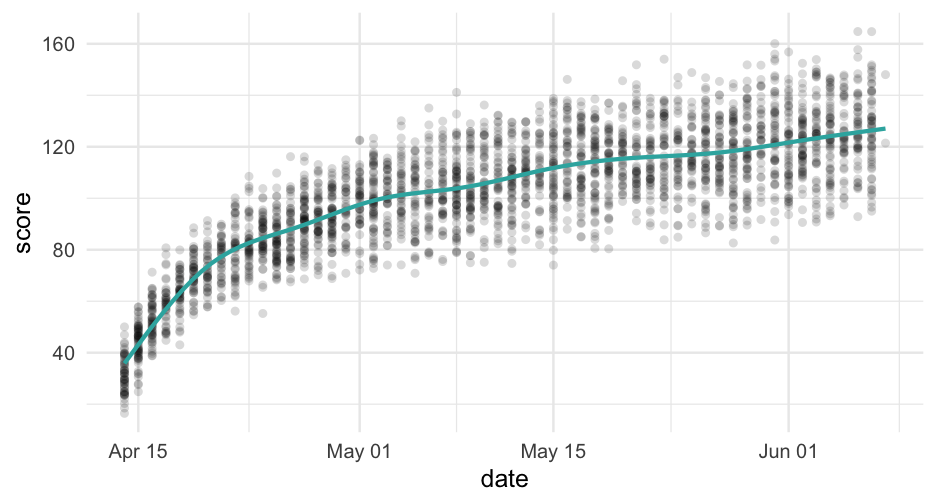
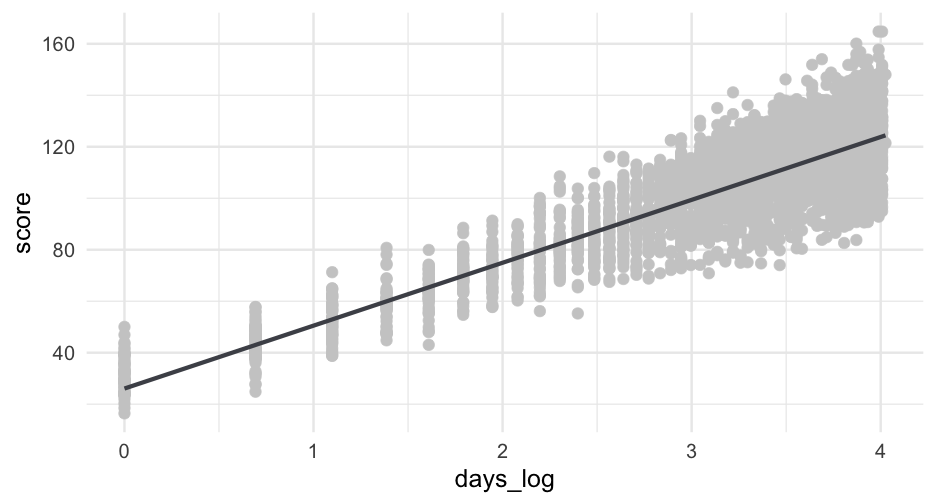
If you're familiar with log growth, the scatterplots we've been looking at probably resemble this trend quite well.

Let's try log transforming our time variable, then fit with it - bonus, we save two estimated parameters.

Note - I will have to use `log(x + 1)` instead of `log(x)` because `log(0)` `$= - \infty$`  and `log(1)` `$= 0$`.

---

```r
sim_d <- sim_d %>% 
  mutate(days_log = log(days_from_start + 1))

log_m <- lmer(score ~ days_log + (days_log|sid), 
              data = sim_d)

arm::display(log_m)
```

```
## lmer(formula = score ~ days_log + (days_log | sid), data = sim_d)
##             coef.est coef.se
## (Intercept) 26.08     0.32  
## days_log    24.43     0.15  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr 
##  sid      (Intercept) 6.16          
##           days_log    3.05     0.20 
##  Residual             1.52          
## ---
## number of obs: 2760, groups: sid, 500
## AIC = 13703.9, DIC = 13687
## deviance = 13689.5
```

---
# Compare

```r
anova(linear, quad, cubic, log_m)
```

```
## refitting model(s) with ML (instead of REML)
```

```
## Data: sim_d
## Models:
## linear: score ~ days_from_start + (days_from_start | sid)
## log_m: score ~ days_log + (days_log | sid)
## quad: score ~ days_from_start + days2 + (days_from_start | sid)
## cubic: score ~ days_from_start + days2 + days3 + (days_from_start | 
## cubic:     sid)
##        npar   AIC   BIC   logLik deviance Chisq Df Pr(>Chisq)    
## linear    6 20999 21035 -10493.7    20987                        
## log_m     6 13702 13737  -6844.7    13690  7298  0               
## quad      7 18259 18301  -9122.6    18245     0  1          1    
## cubic     8 16269 16317  -8126.6    16253  1992  1     <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

It use the same number of parameters as the linear model, but fits *far* better.

---
# Predictions

```r
pred_frame <- pred_frame %>% 
  mutate(days_log = log(days_from_start + 1))

pred_frame <- pred_frame %>% 
  mutate(pred_log = predict(log_m, 
                            newdata = ., 
                            allow.new.levels = TRUE))
```

--
Let's first look at these predictions on the log scale

---
# Predictions on log scale

```r
ggplot(pred_frame, aes(days_log)) +
  geom_point(aes(y = score), data = sim_d, color = "gray80") +
  geom_line(aes(y = pred_log), color = "#4D4F57")
```

![](w6p1_files/figure-html/unnamed-chunk-85-1.png)

---
# On raw scale

```r
pred_frame %>% 
  mutate(pred_cubic = predict(cubic, 
                              newdata = ., 
                              allow.new.levels = TRUE)) %>% 
  ggplot(aes(days_from_start)) +
  geom_point(aes(y = score), data = sim_d, color = "gray80") +
  geom_line(aes(y = pred_linear), color = "#33B1AE") +
  geom_line(aes(y = pred_quad), color = "#808AFF") +
  geom_line(aes(y = pred_cubic), color = "#ff66fa") +
  geom_line(aes(y = pred_log), color = "#4D4F57")
```

---
# On raw scale

![](w6p1_files/figure-html/unnamed-chunk-87-1.png)

---
class: inverse-green middle
# Next time
Bayesian Methods

## Now: Homework 2