Intro to Bayes
Daniel Anderson
Week 7
The data
From an example in the Mplus manual. I made up the column names.
01:30
mplus_d <- read_csv(here::here("data", "mplus920.csv"))mplus_d## # A tibble: 7,500 x 6## score baseline sch_treatment dist_ses schid distid## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 5.559216 1.383101 1 -0.642262 1 1## 2 -0.107394 -0.789654 1 -0.642262 1 1## 3 0.049476 -0.760867 1 -0.642262 1 1## 4 -2.387703 -0.798527 1 -0.642262 1 1## 5 1.180393 -0.411377 1 -0.642262 1 1## 6 3.959005 -0.987154 1 -0.642262 2 1## 7 -0.895792 -1.966773 1 -0.642262 2 1## 8 2.879087 0.42117 1 -0.642262 2 1## 9 5.611088 1.67047 1 -0.642262 2 1## 10 2.828119 0.001154 1 -0.642262 2 1## # … with 7,490 more rowsModel 2
Fit the following model
01:00
scorei∼N(αj[i],k[i]+β1(baseline),σ2)αj∼N(μαj,σ2αj), for schid j = 1,…,Jαk∼N(μαk,σ2αk), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1(baseline),σ2)αj∼N(μαj,σ2αj), for schid j = 1,…,Jαk∼N(μαk,σ2αk), for distid k = 1,…,K
lmer(score ~ baseline + (1|schid) + (1|distid), data = mplus_d)Model 3
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((μαjμβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses)+γα2(baseline×dist_ses),σ2αk), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((μαjμβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses)+γα2(baseline×dist_ses),σ2αk), for distid k = 1,…,K
Model 3
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((μαjμβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses)+γα2(baseline×dist_ses),σ2αk), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((μαjμβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses)+γα2(baseline×dist_ses),σ2αk), for distid k = 1,…,K
lmer(score ~ baseline * dist_ses + (baseline|schid) + (1|distid), data = mplus_d)Model 4
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)μβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses),σ2αk), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)μβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses),σ2αk), for distid k = 1,…,K
Model 4
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)μβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses),σ2αk), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)μβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,Jαk∼N(γα0+γα1(dist_ses),σ2αk), for distid k = 1,…,K
lmer(score ~ baseline + sch_treatment + dist_ses + (baseline|schid) + (1|distid), data = mplus_d)Model 5
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkγ1k)∼N((γα0+γα1(dist_ses)μγ1k),(σ2αkραkγ1kργ1kαkσ2γ1k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkγ1k)∼N((γα0+γα1(dist_ses)μγ1k),(σ2αkραkγ1kργ1kαkσ2γ1k)), for distid k = 1,…,K
Model 5
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkγ1k)∼N((γα0+γα1(dist_ses)μγ1k),(σ2αkραkγ1kργ1kαkσ2γ1k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkγ1k)∼N((γα0+γα1(dist_ses)μγ1k),(σ2αkραkγ1kργ1kαkσ2γ1k)), for distid k = 1,…,K
lmer(score ~ baseline * sch_treatment + dist_ses + (baseline|schid) + (sch_treatment|distid), data = mplus_d)Model 6
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ11k[i0+γβ11k[i](sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1kγ1kγβ11k)∼N((γα0+γα1(dist_ses)μβ1kμγ1kμγβ11k),(σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ11k[i0+γβ11k[i](sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J⎛⎜ ⎜ ⎜ ⎜⎝αkβ1kγ1kγβ11k⎞⎟ ⎟ ⎟ ⎟⎠∼N⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝⎛⎜ ⎜ ⎜ ⎜⎝γα0+γα1(dist_ses)μβ1kμγ1kμγβ11k⎞⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠, for distid k = 1,…,K
Model 6
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ11k[i0+γβ11k[i](sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1kγ1kγβ11k)∼N((γα0+γα1(dist_ses)μβ1kμγ1kμγβ11k),(σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1k[i](sch_treatment)γβ11k[i0+γβ11k[i](sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J⎛⎜ ⎜ ⎜ ⎜⎝αkβ1kγ1kγβ11k⎞⎟ ⎟ ⎟ ⎟⎠∼N⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝⎛⎜ ⎜ ⎜ ⎜⎝γα0+γα1(dist_ses)μβ1kμγ1kμγβ11k⎞⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠, for distid k = 1,…,K
lmer(score ~ baseline * sch_treatment + dist_ses + (baseline|schid) + (baseline * sch_treatment||distid), data = mplus_d)Final one
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1k)∼N((γα0+γα1(dist_ses)+γα2(dist_ses×sch_treatment)γβ10+γβ11(dist_ses)+γβ11(dist_ses×sch_treatment)),(σ2αkραkβ1kρβ1kαkσ2β1k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1k)∼N((γα0+γα1(dist_ses)+γα2(dist_ses×sch_treatment)γβ10+γβ11(dist_ses)+γβ11(dist_ses×sch_treatment)),(σ2αkραkβ1kρβ1kαkσ2β1k)), for distid k = 1,…,K
Final one
Fit the following model
01:30
scorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1k)∼N((γα0+γα1(dist_ses)+γα2(dist_ses×sch_treatment)γβ10+γβ11(dist_ses)+γβ11(dist_ses×sch_treatment)),(σ2αkραkβ1kρβ1kαkσ2β1k)), for distid k = 1,…,Kscorei∼N(αj[i],k[i]+β1j[i],k[i](baseline),σ2)(αjβ1j)∼N((γα0+γα1(sch_treatment)γβ10+γβ11(sch_treatment)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for schid j = 1,…,J(αkβ1k)∼N((γα0+γα1(dist_ses)+γα2(dist_ses×sch_treatment)γβ10+γβ11(dist_ses)+γβ11(dist_ses×sch_treatment)),(σ2αkραkβ1kρβ1kαkσ2β1k)), for distid k = 1,…,K
lmer(score ~ baseline * sch_treatment * dist_ses + (baseline|schid) + (baseline |distid), data = mplus_d)A disclaimer
There is no chance we'll really be able to do Bayes justice in this class
The hope for today is that you'll get an introduction
By the end you should be able to fit the models you already can, but in a Bayes framework
Hopefully you also recognize the tradeoffs, and potential extensions
In equation form
You'll see this presented many different ways, perhaps mostly commonly as
p(B∣A)=p(A∣B)×p(B)p(A)p(B∣A)=p(A∣B)×p(B)p(A) where ∣∣ is read as "given" and pp is the probability
I prefer to give AA and BB more meaningful names
p(prior∣data)=p(data∣prior)×p(prior)datap(prior∣data)=p(data∣prior)×p(prior)data
A real example
Classifying a student with a learning disability. We want to know
p(LD∣Testp)=p(Testp∣LD)×p(LD)Testpp(LD∣Testp)=p(Testp∣LD)×p(LD)TestpNotice, this means we need to know:
- True positive rate of the test, p(Testp∣LD)p(Testp∣LD)
Base rate for learning disabilities, p(LD)p(LD)
Base rate for testing positive, TestpTestp
Example with IQ
This example borrowed from TJ Mahr
#install.packages("carData")iqs <- carData::Burt$IQbioiqs## [1] 82 80 88 108 116 117 132 71 75 93 95 88 111 63 77 86 83 93 97 87 94 96 112 113 106 107 98Example with IQ
This example borrowed from TJ Mahr
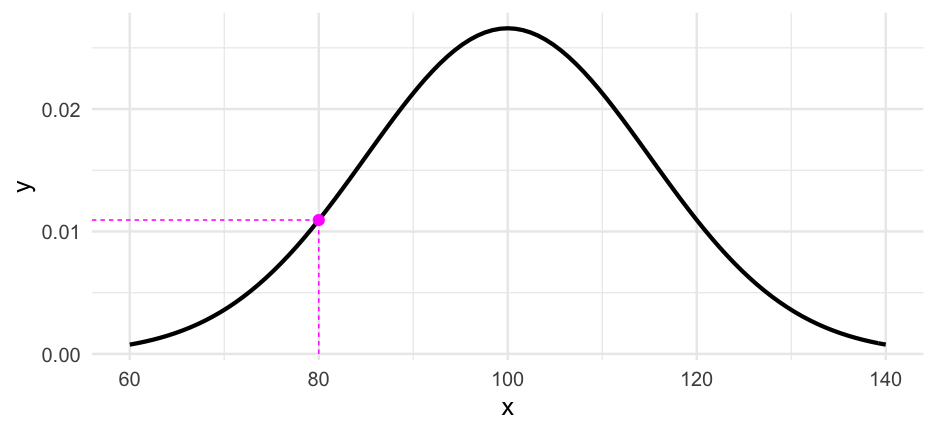
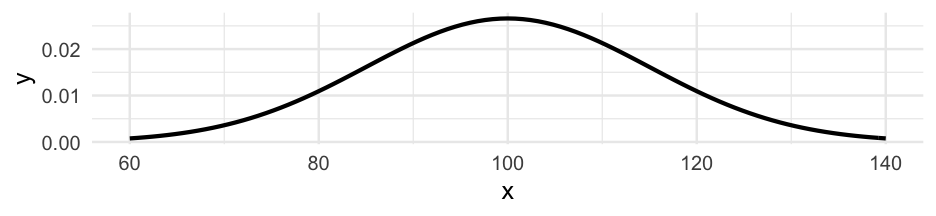
#install.packages("carData")iqs <- carData::Burt$IQbioiqs## [1] 82 80 88 108 116 117 132 71 75 93 95 88 111 63 77 86 83 93 97 87 94 96 112 113 106 107 98IQ scores are generally assumed to be generated from a distribution that looks like this:
IQi∼N(100,15)IQi∼N(100,15)
Example with IQ
This example borrowed from TJ Mahr
#install.packages("carData")iqs <- carData::Burt$IQbioiqs## [1] 82 80 88 108 116 117 132 71 75 93 95 88 111 63 77 86 83 93 97 87 94 96 112 113 106 107 98IQ scores are generally assumed to be generated from a distribution that looks like this:
IQi∼N(100,15)IQi∼N(100,15)
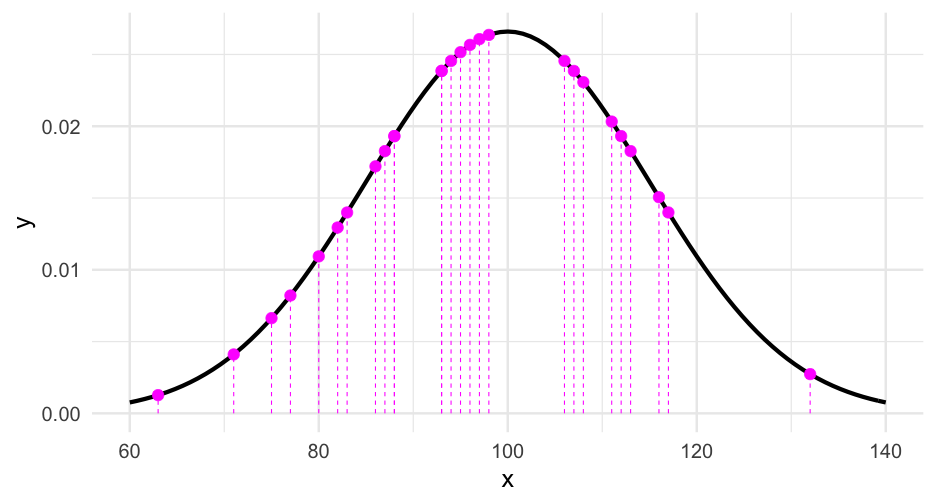
Likelihood of the data
We sum the likelihood to get the overall likelihood of the data. However, this leads to very small numbers. Computationally, it's easier to sum the log of these likelihoods.
dnorm(iqs, mean = 100, sd = 15, log = TRUE)## [1] -4.346989 -4.515878 -3.946989 -3.769211 -4.195878 -4.269211 -5.902544 -5.495878 -5.015878 -3.735878 -3.682544 -3.946989 -3.895878 -6.669211 -4.802544## [16] -4.062544 -4.269211 -3.735878 -3.646989 -4.002544 -3.706989 -3.662544 -3.946989 -4.002544 -3.706989 -3.735878 -3.635878Likelihood of the data
We sum the likelihood to get the overall likelihood of the data. However, this leads to very small numbers. Computationally, it's easier to sum the log of these likelihoods.
dnorm(iqs, mean = 100, sd = 15, log = TRUE)## [1] -4.346989 -4.515878 -3.946989 -3.769211 -4.195878 -4.269211 -5.902544 -5.495878 -5.015878 -3.735878 -3.682544 -3.946989 -3.895878 -6.669211 -4.802544## [16] -4.062544 -4.269211 -3.735878 -3.646989 -4.002544 -3.706989 -3.662544 -3.946989 -4.002544 -3.706989 -3.735878 -3.635878sum(dnorm(iqs, mean = 100, sd = 15, log = TRUE))## [1] -114.3065Alternative distributions
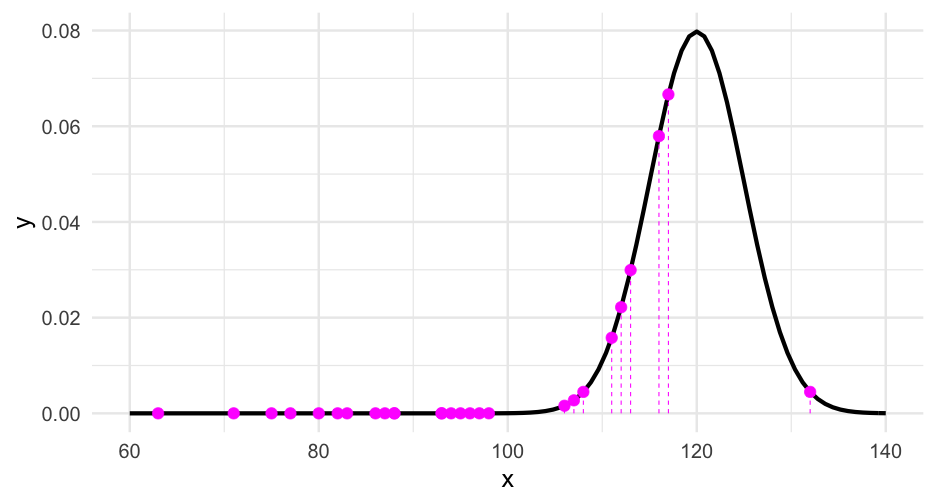
What if we assumed the data were generated from an alternative distribution, say IQi∼N(115,5)IQi∼N(115,5)?
sum(dnorm(iqs, mean = 115, sd = 5, log = TRUE))## [1] -416.3662The value is much lower. In most models, we are estimating μμ and σσ, and trying to find values that maximize the sum of the log likelihoods.
Example
I know we've talked about this before, but a simple linear regression model like this
m <- lm(IQbio ~ class, data = carData::Burt)is generally displayed like this
IQbio=α+β1(classlow)+β2(classmedium)+ϵIQbio=α+β1(classlow)+β2(classmedium)+ϵ
But we could display the same thing like this IQbio∼N(ˆμ,ˆσ)ˆμ=α+β1(classlow)+β2(classmedium)IQbio∼N(ˆμ,ˆσ)ˆμ=α+β1(classlow)+β2(classmedium)
Bayesian posterior
posterior=likelihood×prioraverage likelihoodposterior=likelihood×prioraverage likelihood
The above is how we estimate with Bayes.
In words, it states that our updated beliefs (posterior) depend on the evidence from our data (likelihood) and our prior knowledge/conceptions/information (prior).
Bayesian posterior
posterior=likelihood×prioraverage likelihoodposterior=likelihood×prioraverage likelihood
The above is how we estimate with Bayes.
In words, it states that our updated beliefs (posterior) depend on the evidence from our data (likelihood) and our prior knowledge/conceptions/information (prior).
Our prior will shift in accordance with the evidence from the data
Grid search
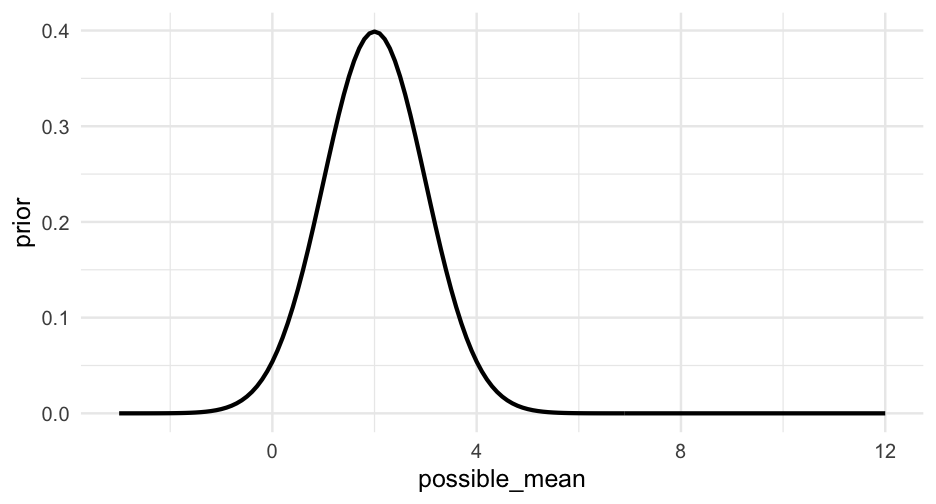
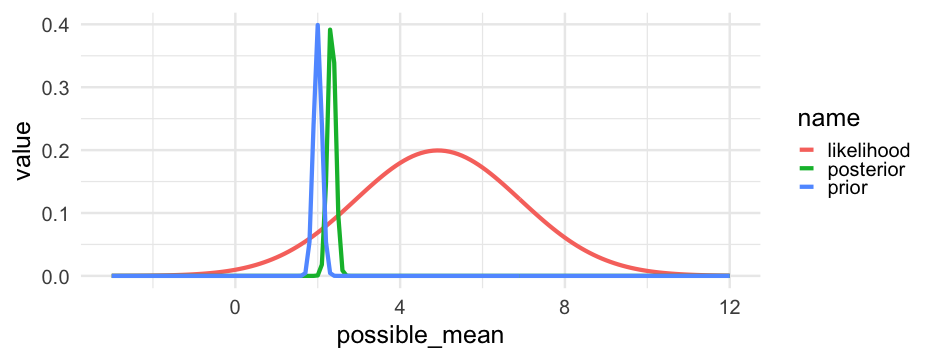
We're now going to specify a grid of possible means for our data. Let's search anywhere from -3 to 12 in 0.1 intervals.
grid <- tibble(possible_mean = seq(-3, 12, 0.1))Next, we'll specify a prior distribution. That is - how likely do we think each of these possible means are?
Let's say our best guess is μ=2μ=2. Values on either side of 22 should be less likely.
Grid search
We're now going to specify a grid of possible means for our data. Let's search anywhere from -3 to 12 in 0.1 intervals.
grid <- tibble(possible_mean = seq(-3, 12, 0.1))Next, we'll specify a prior distribution. That is - how likely do we think each of these possible means are?
Let's say our best guess is μ=2μ=2. Values on either side of 22 should be less likely.
prior <- dnorm(grid$possible_mean, mean = 2, sd = 1)Look at other priors
grid %>% mutate(prior1 = dnorm(possible_mean, mean = 2, sd = 1), prior2 = dnorm(possible_mean, mean = 2, sd = 2), prior3 = dnorm(possible_mean, mean = 2, sd = 3)) %>% ggplot(aes(possible_mean)) + geom_line(aes(y = prior1)) + geom_line(aes(y = prior2), color = "cornflowerblue") + geom_line(aes(y = prior3), color = "firebrick")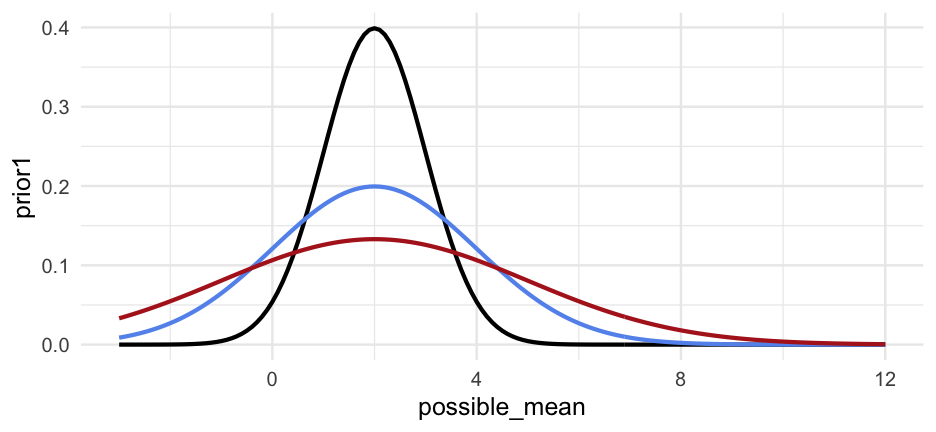
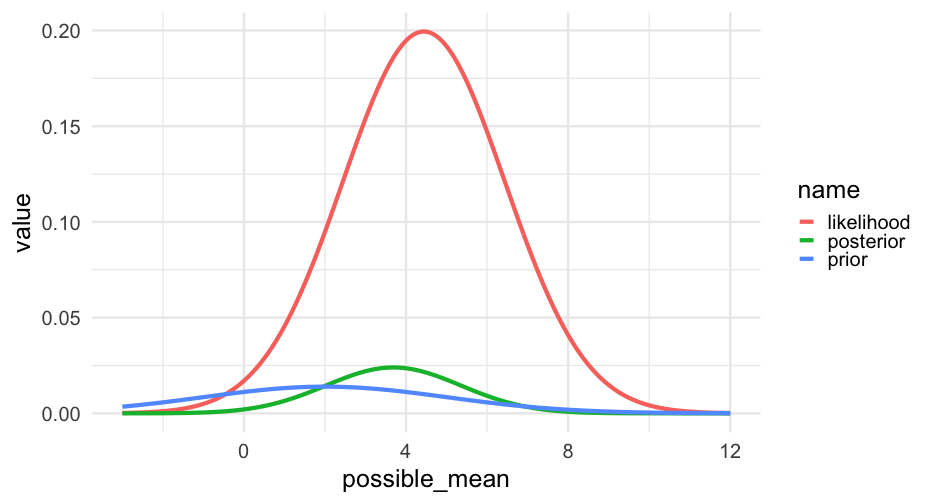
Observe 1 data point
grid <- grid %>% mutate(likelihood = dnorm(true_data[1], possible_mean, 2))grid## # A tibble: 151 x 3## possible_mean prior likelihood## <dbl> <dbl> <dbl>## 1 -3 0.003477802 0.0001973758## 2 -2.9 0.003674439 0.0002374240## 3 -2.8 0.003877883 0.0002848850## 4 -2.7 0.004088046 0.0003409800## 5 -2.6 0.004304813 0.0004071013## 6 -2.5 0.004528041 0.0004848308## 7 -2.4 0.004757554 0.0005759600## 8 -2.3 0.004993151 0.0006825094## 9 -2.2 0.005234594 0.0008067505## 10 -2.1 0.005481619 0.0009512268## # … with 141 more rowsAll the data
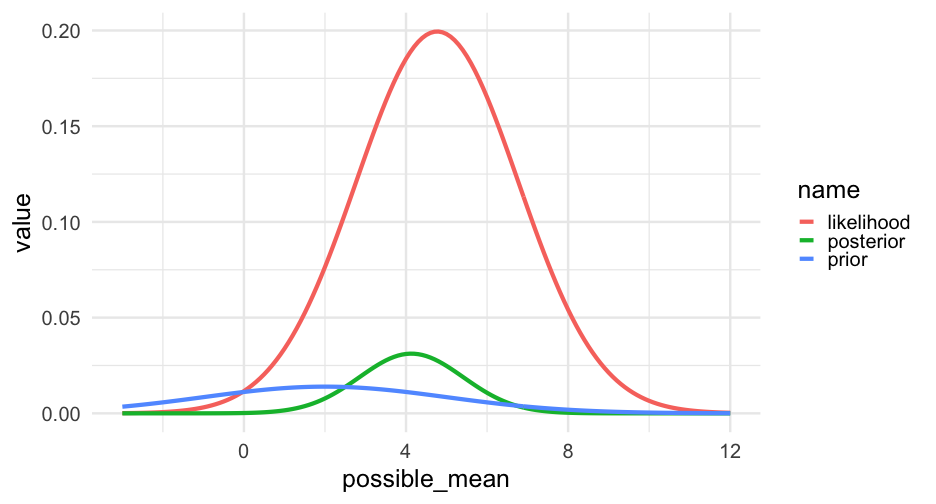
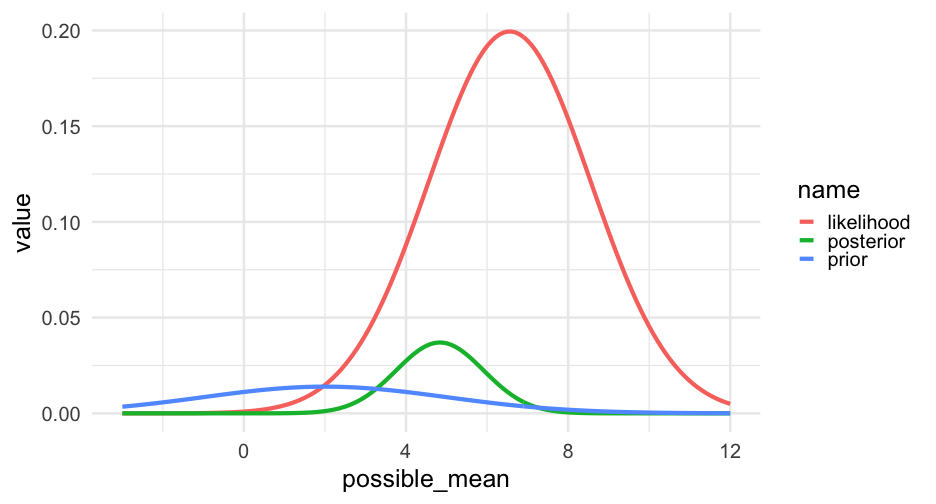
grid <- grid %>% mutate(prior = dnorm(grid$possible_mean, mean = 2, sd = 3), prior = prior / sum(prior), posterior = prior) # best guess before seeing datafor(i in seq_along(true_data)) { grid <- grid %>% mutate(likelihood = dnorm(true_data[i], possible_mean, 2), posterior = likelihood * posterior, posterior = posterior / sum(posterior))}Sampling
Now that we have a posterior distribution, we can sample from it to help us with inference
Each possible mean should be sampled in accordance with its probability specified by the posterior.
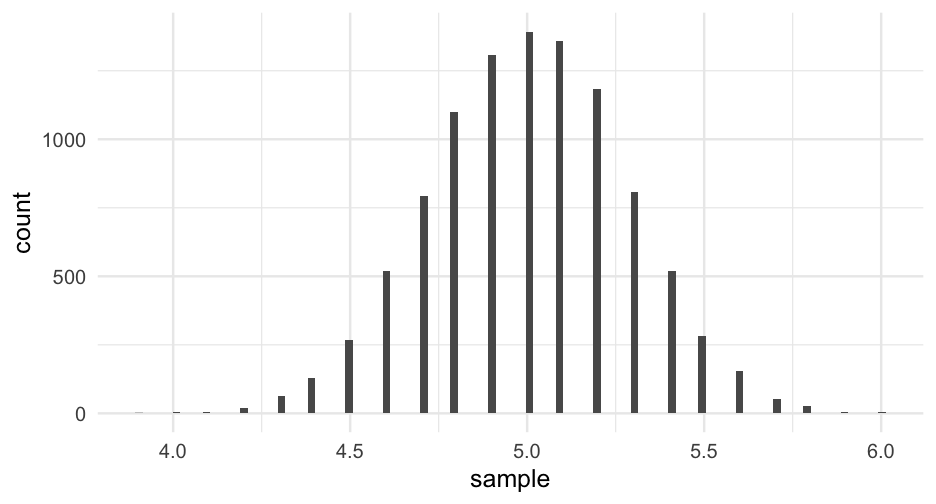
- Let's draw 10,000 samples
posterior_samples <- sample(grid$possible_mean, size = 10000, replace = TRUE, prob = grid$posterior)Credible intervals
Let's compute an 80% credible interval
tibble(posterior_samples) %>% summarize(ci_80 = quantile(posterior_samples, c(0.1, 0.9)))## # A tibble: 2 x 1## ci_80## <dbl>## 1 4.6## 2 5.4What's the chance the "true" mean is less than 4.8?
sum(posterior_samples < 4.8) / length(posterior_samples) * 100## [1] 18.05Ranges
What's the probability the "true" mean is between 5.2 and 5.5?
sum(posterior_samples >= 5.2 & posterior_samples <= 5.5) / length(posterior_samples) * 100## [1] 27.94Greater than 4.5?
sum(posterior_samples > 4.5) / length(posterior_samples) * 100## [1] 95.05Note this is much more natural than frequentist statistics
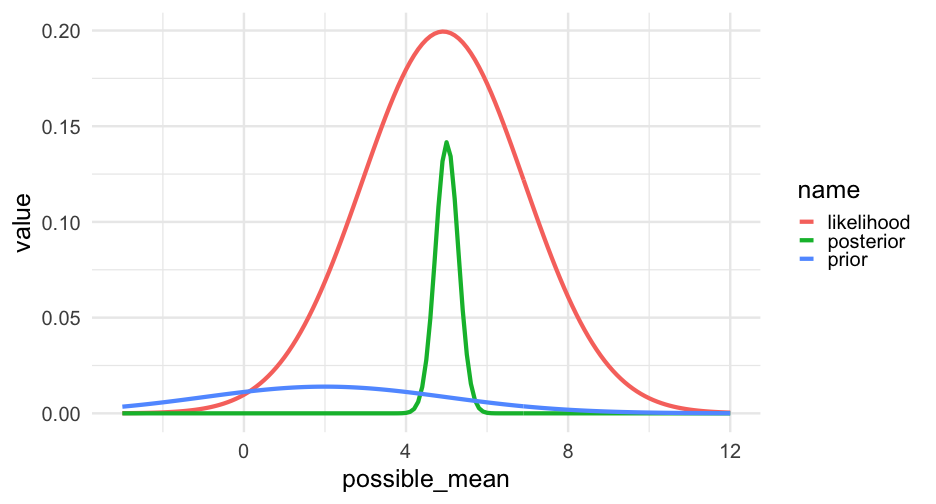
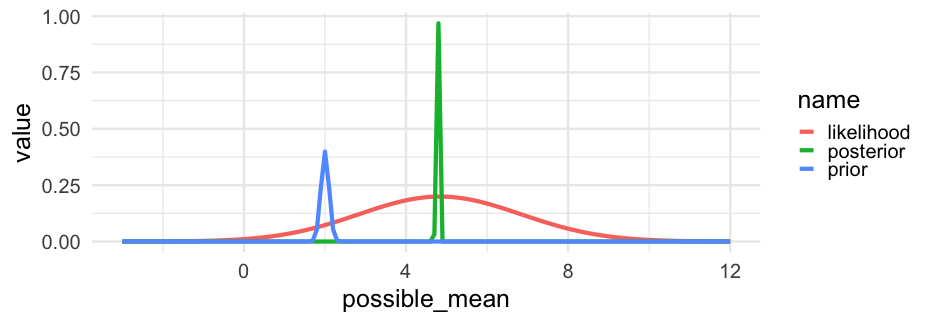
Change our prior
Let's try again with a tighter prior
grid <- grid %>% mutate(prior = dnorm(grid$possible_mean, mean = 2, sd = 0.1), prior = prior / sum(prior), posterior = prior) # best guess before seeing datafor(i in seq_along(true_data)) { grid <- grid %>% mutate(likelihood = dnorm(true_data[i], possible_mean, 2), posterior = likelihood * posterior, posterior = posterior / sum(posterior))}true_data <- rnorm(5000, 5, 1)grid <- grid %>% mutate(prior = dnorm(grid$possible_mean, mean = 2, sd = 0.1), prior = prior / sum(prior), posterior = prior) # best guess before seeing datafor(i in seq_along(true_data)) { grid <- grid %>% mutate(likelihood = dnorm(true_data[i], possible_mean, 2), posterior = likelihood * posterior, posterior = posterior / sum(posterior))}Taking a step back
The purpose of the prior is to include what you already know into your analysis
The strength of your prior should depend on your prior research
Larger samples will overwhelm priors quicker, particularly if they are diffuse
Think through the lens of updating your prior beliefs
This whole framework is quite different, but also gives us a lot of advantages in terms of probability interpretation, as we'll see
More complicated
- Remember our posterior is defined by
posterior=likelihood×prioraverage likelihoodposterior=likelihood×prioraverage likelihood When we just had a single parameter to estimate, μμ, this was tractable with grid search.
With even simple linear regression, however, we have three parameters: αα, ββ, and σσ
More complicated
- Remember our posterior is defined by
posterior=likelihood×prioraverage likelihoodposterior=likelihood×prioraverage likelihood When we just had a single parameter to estimate, μμ, this was tractable with grid search.
With even simple linear regression, however, we have three parameters: αα, ββ, and σσ
Our Bayesian model then becomes considerably more complicated:
P(α,β,σ∣x)=P(x∣α,β,σ)P(α,β,σ)∭P(x∣α,β,σ)P(α,β,σ)dαdβdσP(α,β,σ∣x)=P(x∣α,β,σ)P(α,β,σ)∭P(x∣α,β,σ)P(α,β,σ)dαdβdσ
Conceptually
Imagine the posterior as a hill
We start with the parameters set to random numbers
- Estimate the posterior with this values (our spot on the hill)
Use information from the prior sample to determine whether and how to change the current parameter values
Try to "walk" around in a way to a complete "picture" of the hill from the samples
Use these samples as your posterior distribution
Metropolis-Hastings
We will use is called the Metropolis-Hastings algorithm:
Compute a candidate "step" for the parameters
Calculate an acceptance ratio α=f(x′)/f(xt). This will fall between 0 and 1.
Generate number, u, from a random uniform distribution between 0 and 1
if u≤α, accept the candidate
if u≥α, reject the candidate
Metropolis-Hastings
We will use is called the Metropolis-Hastings algorithm:
Compute a candidate "step" for the parameters
Calculate an acceptance ratio α=f(x′)/f(xt). This will fall between 0 and 1.
Generate number, u, from a random uniform distribution between 0 and 1
if u≤α, accept the candidate
if u≥α, reject the candidate
Complicated, but conceptually we're trying to sample the joint posterior distribution in a way that conforms with the probability density of the posterior (i.e., the shape)