More Bayes
And multilevel binomial logistic regression
Daniel Anderson
Week 8
The data
Read in the following data
library(tidyverse)library(lme4)d <- read_csv(here::here("data", "three-lev.csv"))d## # A tibble: 7,230 x 12## schid sid size lowinc mobility female black hispanic retained grade year math## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 2020 273026452 380 40.3 12.5 0 0 1 0 2 0.5 1.146## 2 2020 273026452 380 40.3 12.5 0 0 1 0 3 1.5 1.134## 3 2020 273026452 380 40.3 12.5 0 0 1 0 4 2.5 2.3 ## 4 2020 273030991 380 40.3 12.5 0 0 0 0 0 -1.5 -1.303## 5 2020 273030991 380 40.3 12.5 0 0 0 0 1 -0.5 0.439## 6 2020 273030991 380 40.3 12.5 0 0 0 0 2 0.5 2.43 ## 7 2020 273030991 380 40.3 12.5 0 0 0 0 3 1.5 2.254## 8 2020 273030991 380 40.3 12.5 0 0 0 0 4 2.5 3.873## 9 2020 273059461 380 40.3 12.5 0 0 1 0 0 -1.5 -1.384## 10 2020 273059461 380 40.3 12.5 0 0 1 0 1 -0.5 0.338## # … with 7,220 more rowsModel 3
Fit the following model
01:30
mathi∼N(αj[i],k[i]+β1j[i](year),σ2)(αjβ1j)∼N((γα0+γα1(black)+γα2(hispanic)+γα3(female)γβ10+γβ11(black)+γβ12(hispanic)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,Jαk∼N(γα0+γα1(mobility),σ2αk), for schid k = 1,…,K
lmer(math ~ year * black + year * hispanic + female + mobility + (year|sid) + (1|schid), data = d)Model 4
Fit the following model
01:30
mathi∼N(αj[i],k[i]+β1j[i],k[i](year),σ2)(αjβ1j)∼N((γα0+γα1k[i](female)γβ10+γβ11(female)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,J⎛⎜⎝αkβ1kγ1k⎞⎟⎠∼N⎛⎜ ⎜⎝⎛⎜ ⎜⎝γα0+γα1(mobility)+γα2(lowinc)γβ10+γβ11(mobility)μγ1k⎞⎟ ⎟⎠,⎛⎜ ⎜⎝σ2αkραkβ1kραkγ1kρβ1kαkσ2β1kρβ1kγ1kργ1kαkργ1kβ1kσ2γ1k⎞⎟ ⎟⎠⎞⎟ ⎟⎠, for schid k = 1,…,K
Model 4
Fit the following model
01:30
mathi∼N(αj[i],k[i]+β1j[i],k[i](year),σ2)(αjβ1j)∼N((γα0+γα1k[i](female)γβ10+γβ11(female)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,J⎛⎜⎝αkβ1kγ1k⎞⎟⎠∼N⎛⎜ ⎜⎝⎛⎜ ⎜⎝γα0+γα1(mobility)+γα2(lowinc)γβ10+γβ11(mobility)μγ1k⎞⎟ ⎟⎠,⎛⎜ ⎜⎝σ2αkραkβ1kραkγ1kρβ1kαkσ2β1kρβ1kγ1kργ1kαkργ1kβ1kσ2γ1k⎞⎟ ⎟⎠⎞⎟ ⎟⎠, for schid k = 1,…,K
lmer(math ~ year * female + year * mobility + lowinc + (year|sid) + (year + female|schid), data = d)Model 5
Fit the following model
Don't worry if you run into convergene warnings
01:30
mathi∼N(αj[i],k[i]+β1j[i],k[i](year),σ2)(αjβ1j)∼N((γα0+γα1k[i](female)γβ11k[i0+γβ11k[i](female)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,J⎛⎜ ⎜ ⎜ ⎜⎝αkβ1kγ1kγβ11k⎞⎟ ⎟ ⎟ ⎟⎠∼N⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝⎛⎜ ⎜ ⎜ ⎜⎝γα0+γα1(mobility)+γα2(lowinc)μβ1kμγ1kμγβ11k⎞⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠, for schid k = 1,…,K
Model 5
Fit the following model
Don't worry if you run into convergene warnings
01:30
mathi∼N(αj[i],k[i]+β1j[i],k[i](year),σ2)(αjβ1j)∼N((γα0+γα1k[i](female)γβ11k[i0+γβ11k[i](female)),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,J⎛⎜ ⎜ ⎜ ⎜⎝αkβ1kγ1kγβ11k⎞⎟ ⎟ ⎟ ⎟⎠∼N⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝⎛⎜ ⎜ ⎜ ⎜⎝γα0+γα1(mobility)+γα2(lowinc)μβ1kμγ1kμγβ11k⎞⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝σ2αk0000σ2β1k0000σ2γ1k0000σ2γβ11k⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠, for schid k = 1,…,K
lmer(math ~ year * female + mobility + lowinc + (year|sid) + (year * female||schid), data = d)Model 8
Last one
01:30
mathi∼N(αj[i],k[i]+β1j[i],k[i](year),σ2)(αjβ1j)∼N((γα0+γα1(female)μβ1j),(σ2αjραjβ1jρβ1jαjσ2β1j)), for sid j = 1,…,J(αkβ1k)∼N((γα0+γα1(lowinc)γβ10+γβ11(lowinc)),(σ2αkραkβ1kρβ1kαkσ2β1k)), for schid k = 1,…,K
lmer(math ~ year * lowinc + female + (year|sid) + (year |schid), data = d)Updated beliefs
- Remember our posterior is defined by
posterior=likelihood×prioraverage likelihood When we just had a single parameter to estimate, μ, this was tractable with grid search.
With even simple linear regression, however, we have three parameters: α, β, and σ
Our Bayesian model then becomes considerably more complicated:
P(α,β,σ∣x)=P(x∣α,β,σ)P(α,β,σ)∭P(x∣α,β,σ)P(α,β,σ)dαdβdσ
Conceptually
Imagine the posterior as a hill
We start with the parameters set to random numbers
- Estimate the posterior with this values (our spot on the hill)
Try to "walk" around in a way that we get a complete "picture" of the hill from the samples
Use these samples as your posterior distribution
An example
Example from Ravenzwaaij et al.
Let's go back to an example where we're trying to estimate the mean with a know standard deviation.
An example
Example from Ravenzwaaij et al.
Let's go back to an example where we're trying to estimate the mean with a know standard deviation. N(μ,15)
An example
Example from Ravenzwaaij et al.
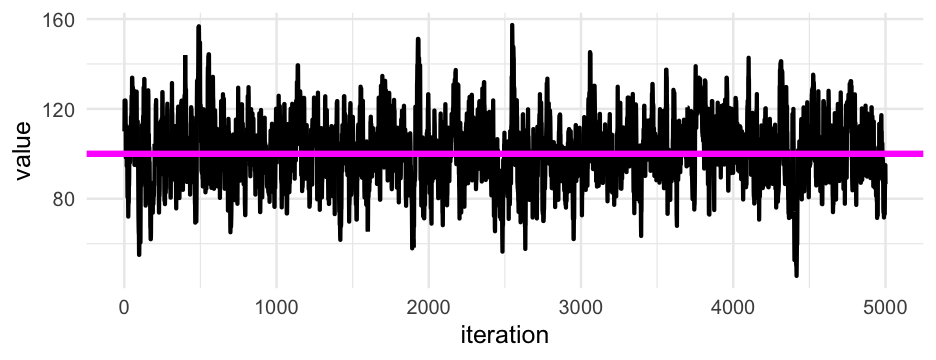
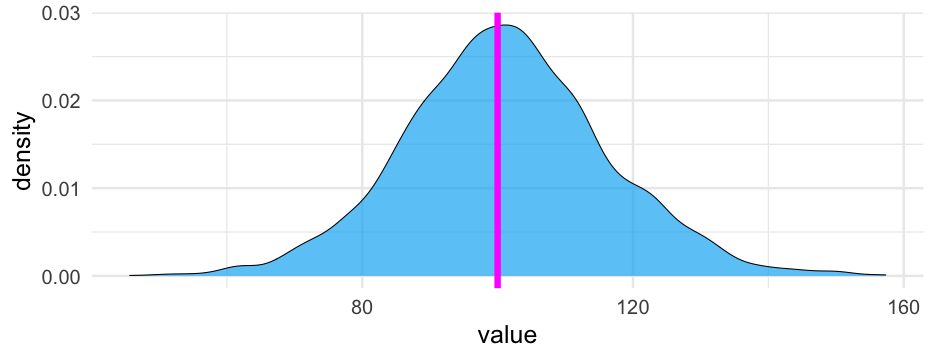
Let's go back to an example where we're trying to estimate the mean with a know standard deviation. N(μ,15) Start with an initial guess, say 110
MCMC
One algorithm:
Generate a proposal by taking a sample from your best guess according to some distribution, e.g., proposal∼N(110,10). Suppose we get a value of 108
Observe the actual data. Let's say we have only one point: 100
- Compare the "height" of the proposal distribution to height of the current distribution, relative to observed data: N(100|110,15), N(100|108,15)
If probability of target distribution is higher, accept
If probability is lower, randomly select between the two with probability equal to the "heights" (probability of the two distributions)
If proposal is accepted - it's the next sample in the chain
Otherwise, the next sample is a copy of current sample
If probability of target distribution is higher, accept
If probability is lower, randomly select between the two with probability equal to the "heights" (probability of the two distributions)
If proposal is accepted - it's the next sample in the chain
Otherwise, the next sample is a copy of current sample
This completes one iteration
Next iteration starts by generating a new proposal distribution
If probability of target distribution is higher, accept
If probability is lower, randomly select between the two with probability equal to the "heights" (probability of the two distributions)
If proposal is accepted - it's the next sample in the chain
Otherwise, the next sample is a copy of current sample
This completes one iteration
Next iteration starts by generating a new proposal distribution
Stop when you have enough samples to have an adequate "picture"
Loop
for(i in 2:5000) { # generate proposal distribution proposal <- rnorm(1, mean = samples[i - 1], sd = 10) # calculate current/proposal distribution likelihoood prob_current <- dnorm(samples[i - 1], 100, 15) prob_proposal <- dnorm(proposal, 100, 15) # compute the probability ratio prob_ratio <- prob_proposal / prob_current # Determine which to select if(prob_ratio > runif(1)) { samples[i] <- proposal # accept } else { samples[i] <- samples[i - 1] # reject }}What is it?
bayesian regression modeling with stan
Uses stan as the model backend - basically writes the model code for you then sends it to stan
Allows model syntax similar to lme4
Simple specification of priors - defaults are flat
Provides many methods for post-model fitting inference
Fit a basic model
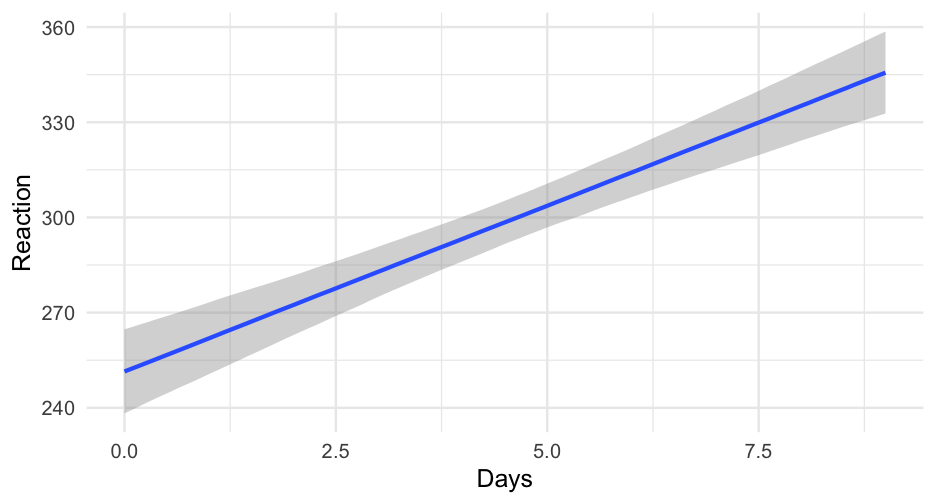
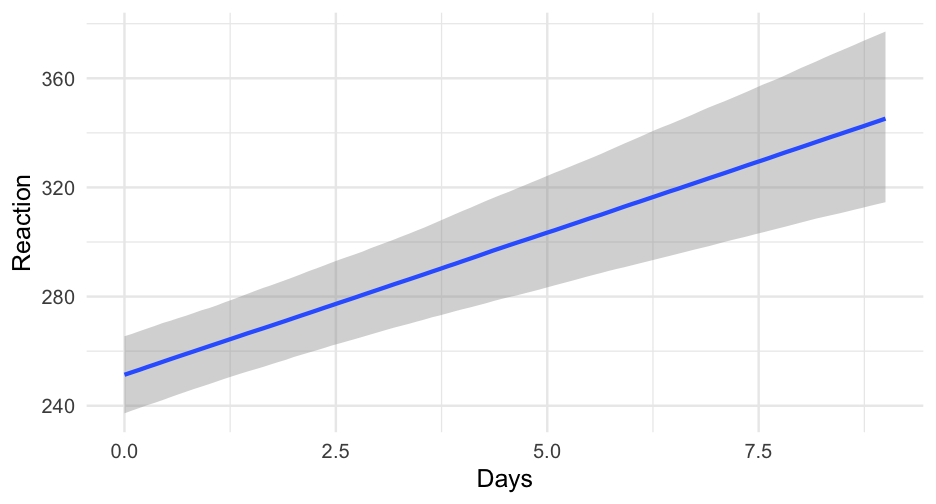
Let's start with the default (uninformative) priors, and fit a standard, simple-linear regression model
library(brms)sleep_m0 <- brm(Reaction ~ Days, data = lme4::sleepstudy)## ## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 1).## Chain 1: ## Chain 1: Gradient evaluation took 2.2e-05 seconds## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.22 seconds.## Chain 1: Adjust your expectations accordingly!## Chain 1: ## Chain 1: ## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)## Chain 1: ## Chain 1: Elapsed Time: 0.050609 seconds (Warm-up)## Chain 1: 0.017419 seconds (Sampling)## Chain 1: 0.068028 seconds (Total)## Chain 1: ## ## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 2).## Chain 2: ## Chain 2: Gradient evaluation took 6e-06 seconds## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.## Chain 2: Adjust your expectations accordingly!## Chain 2: ## Chain 2: ## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)## Chain 2: ## Chain 2: Elapsed Time: 0.048009 seconds (Warm-up)## Chain 2: 0.021626 seconds (Sampling)## Chain 2: 0.069635 seconds (Total)## Chain 2: ## ## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 3).## Chain 3: ## Chain 3: Gradient evaluation took 1.2e-05 seconds## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.## Chain 3: Adjust your expectations accordingly!## Chain 3: ## Chain 3: ## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)## Chain 3: ## Chain 3: Elapsed Time: 0.041524 seconds (Warm-up)## Chain 3: 0.020323 seconds (Sampling)## Chain 3: 0.061847 seconds (Total)## Chain 3: ## ## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 4).## Chain 4: ## Chain 4: Gradient evaluation took 7e-06 seconds## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds.## Chain 4: Adjust your expectations accordingly!## Chain 4: ## Chain 4: ## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)## Chain 4: ## Chain 4: Elapsed Time: 0.048884 seconds (Warm-up)## Chain 4: 0.020719 seconds (Sampling)## Chain 4: 0.069603 seconds (Total)## Chain 4:Model summary
summary(sleep_m0)## Family: gaussian ## Links: mu = identity; sigma = identity ## Formula: Reaction ~ Days ## Data: lme4::sleepstudy (Number of observations: 180) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 251.49 6.64 238.26 264.74 1.00 4168 3040## Days 10.45 1.25 7.98 12.90 1.00 4155 2967## ## Family Specific Parameters: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sigma 47.96 2.51 43.34 53.22 1.00 4069 2959## ## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).Multilevel model
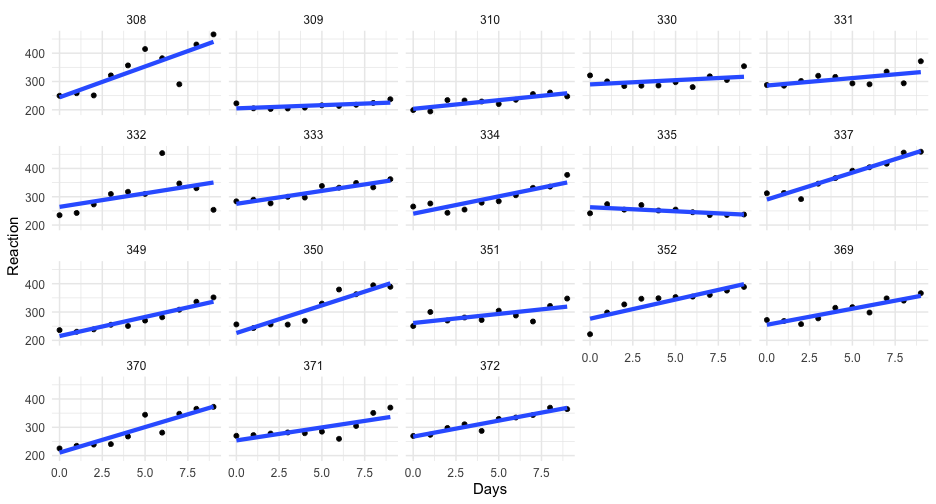
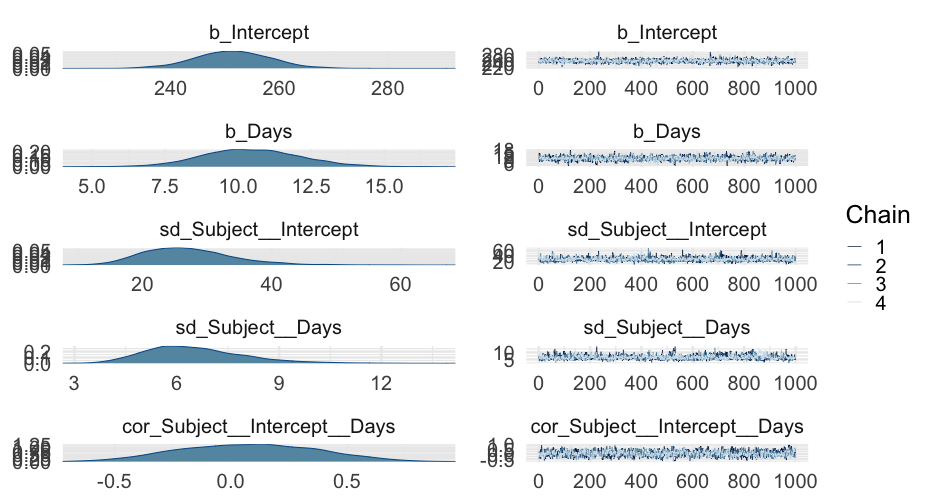
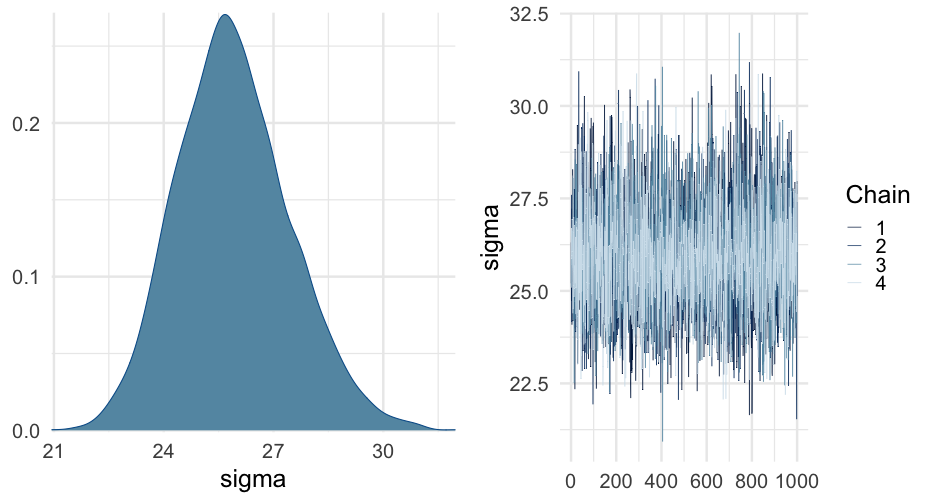
Notice the syntax is essentially equivalent to lme4
sleep_m1 <- brm(Reaction ~ Days + (Days | Subject), data = lme4::sleepstudy)summary(sleep_m1)## Family: gaussian ## Links: mu = identity; sigma = identity ## Formula: Reaction ~ Days + (Days | Subject) ## Data: lme4::sleepstudy (Number of observations: 180) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Group-Level Effects: ## ~Subject (Number of levels: 18) ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sd(Intercept) 27.06 7.15 15.59 42.69 1.00 1529 2353## sd(Days) 6.55 1.49 4.19 10.04 1.00 1144 1440## cor(Intercept,Days) 0.08 0.29 -0.47 0.64 1.01 1125 1844## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 251.42 7.17 237.21 265.47 1.00 2093 2543## Days 10.45 1.71 7.23 13.95 1.00 1660 2090## ## Family Specific Parameters: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sigma 25.91 1.54 23.13 29.17 1.00 3581 2712## ## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).Model comparison
See here for probably the best paper on this topic to date (imo)
Two primary (modern) methods
Leave-one-out Cross-Validation (LOO)
Widely Applicable Information Criterion (WAIC)
Model comparison
See here for probably the best paper on this topic to date (imo)
Two primary (modern) methods
Leave-one-out Cross-Validation (LOO)
Widely Applicable Information Criterion (WAIC)
Both provide estimates of the out-of-sample predictive accuracy of the model. LOO is similar to K-fold CV, while WAIC is similar to AIC/BIC (but an improved version for Bayes models)
Model comparison
See here for probably the best paper on this topic to date (imo)
Two primary (modern) methods
Leave-one-out Cross-Validation (LOO)
Widely Applicable Information Criterion (WAIC)
Both provide estimates of the out-of-sample predictive accuracy of the model. LOO is similar to K-fold CV, while WAIC is similar to AIC/BIC (but an improved version for Bayes models)
Both can be computed using brms. LOO is approximated (not actually refit each time).
LOO: M0
loo(sleep_m0)## ## Computed from 4000 by 180 log-likelihood matrix## ## Estimate SE## elpd_loo -953.3 10.5## p_loo 3.2 0.5## looic 1906.5 21.0## ------## Monte Carlo SE of elpd_loo is 0.0.## ## All Pareto k estimates are good (k < 0.5).## See help('pareto-k-diagnostic') for details.LOO: M1
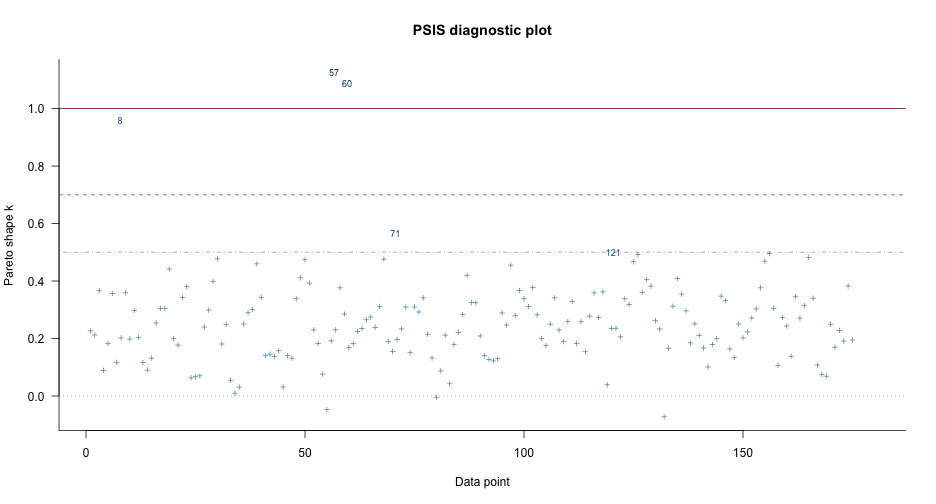
loo(sleep_m1)## Warning: Found 3 observations with a pareto_k > 0.7 in model 'sleep_m1'. It is recommended to set 'moment_match = TRUE' in order to perform moment matching for## problematic observations.## ## Computed from 4000 by 180 log-likelihood matrix## ## Estimate SE## elpd_loo -861.7 22.7## p_loo 34.7 8.8## looic 1723.3 45.5## ------## Monte Carlo SE of elpd_loo is NA.## ## Pareto k diagnostic values:## Count Pct. Min. n_eff## (-Inf, 0.5] (good) 175 97.2% 682 ## (0.5, 0.7] (ok) 2 1.1% 2189 ## (0.7, 1] (bad) 1 0.6% 14 ## (1, Inf) (very bad) 2 1.1% 9 ## See help('pareto-k-diagnostic') for details.LOO Compare
This is a fairly complicated topic, and we won't spend a lot of time on it. See here for a bit more information specifically on the functions
The best fitting model will be on top. Use the standard error within your interpretation
loo_compare(loo(sleep_m0), loo(sleep_m1))## Warning: Found 3 observations with a pareto_k > 0.7 in model 'sleep_m1'. It is recommended to set 'moment_match = TRUE' in order to perform moment matching for## problematic observations.## elpd_diff se_diff## sleep_m1 0.0 0.0 ## sleep_m0 -91.6 21.4WAIC
Similar to other information criteria.
waic(sleep_m0)## ## Computed from 4000 by 180 log-likelihood matrix## ## Estimate SE## elpd_waic -953.3 10.5## p_waic 3.2 0.5## waic 1906.5 21.0waic(sleep_m1)## Warning: ## 14 (7.8%) p_waic estimates greater than 0.4. We recommend trying loo instead.## ## Computed from 4000 by 180 log-likelihood matrix## ## Estimate SE## elpd_waic -860.2 22.3## p_waic 33.2 8.4## waic 1720.5 44.7## ## 14 (7.8%) p_waic estimates greater than 0.4. We recommend trying loo instead.Specifying priors
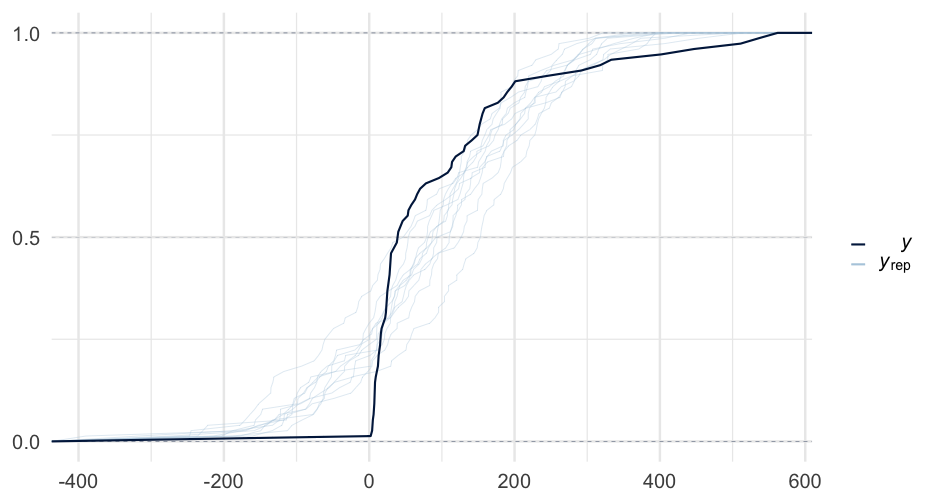
Let's sample from only our priors to see what kind of predictions we get.
Here, we're specifying that our beta coefficient prior is β∼N(0,0.5)
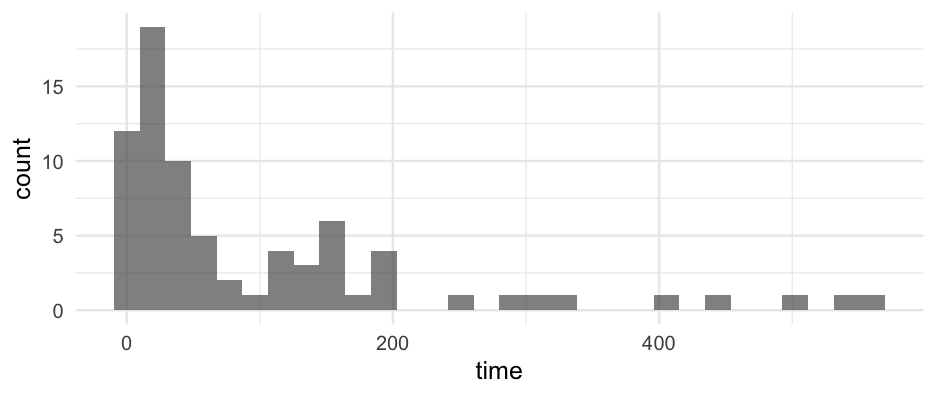
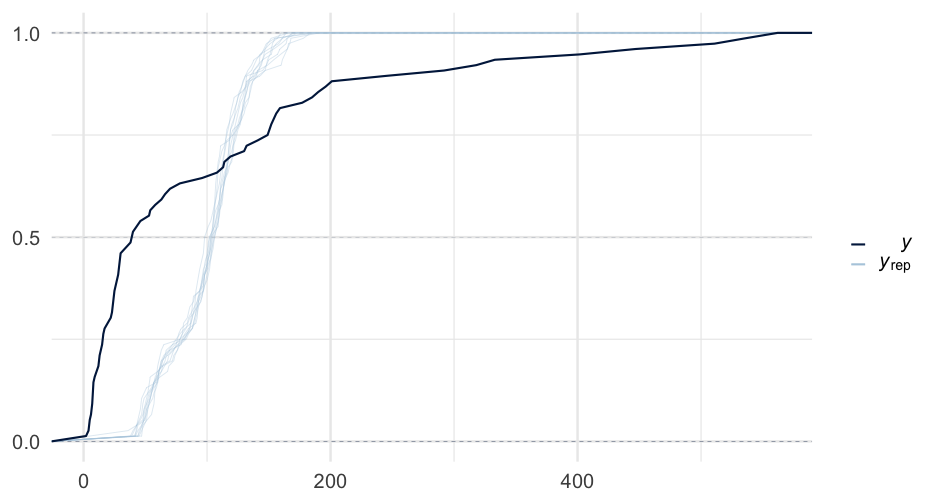
kidney_m3 <- brm( time ~ age + sex, data = kidney, family = Gamma("log"), prior = prior(normal(0, 0.5), class = "b"), sample_prior = "only")kidney_m3## Warning: There were 2253 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-## transitions-after-warmup## Family: gamma ## Links: mu = log; shape = identity ## Formula: time ~ age + sex ## Data: kidney (Number of observations: 76) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 4.23 22.42 -39.94 46.55 1.01 629 991## age -0.02 0.51 -0.97 0.97 1.01 629 946## sexfemale 0.01 0.50 -0.98 0.97 1.01 667 1196## ## Family Specific Parameters: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## shape 0.42 3.64 0.00 2.35 1.01 436 711## ## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).One more model
Let's fit a model we've fit previously
In Week 4, we fit this model
library(lme4)popular <- read_csv(here::here("data", "popularity.csv"))m_lmer <- lmer(popular ~ extrav + (extrav|class), popular, control = lmerControl(optimizer = "bobyqa"))Try fitting the same model with {brms} with the default, diffuse priors
02:00
Bayesian verision
m_brms <- brm(popular ~ extrav + (extrav|class), popular)## Family: gaussian ## Links: mu = identity; sigma = identity ## Formula: popular ~ extrav + (extrav | class) ## Data: popular (Number of observations: 2000) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Group-Level Effects: ## ~class (Number of levels: 100) ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sd(Intercept) 1.72 0.17 1.41 2.08 1.00 1165 2052## sd(extrav) 0.16 0.03 0.11 0.22 1.01 724 1755## cor(Intercept,extrav) -0.95 0.03 -1.00 -0.89 1.01 358 564## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 2.46 0.20 2.06 2.84 1.00 994 1951## extrav 0.49 0.03 0.44 0.54 1.00 1510 2474## ## Family Specific Parameters: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sigma 0.95 0.02 0.92 0.98 1.00 4787 2392## ## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).lme4 model
arm::display(m_lmer)## lmer(formula = popular ~ extrav + (extrav | class), data = popular, ## control = lmerControl(optimizer = "bobyqa"))## coef.est coef.se## (Intercept) 2.46 0.20 ## extrav 0.49 0.03 ## ## Error terms:## Groups Name Std.Dev. Corr ## class (Intercept) 1.73 ## extrav 0.16 -0.97 ## Residual 0.95 ## ---## number of obs: 2000, groups: class, 100## AIC = 5791.4, DIC = 5762## deviance = 5770.7Add priors
Multiple ways to do this
Generally, I allow the intercept to just be what it is
For "fixed" effects, you might consider regularizing priors.
You can also set priors for individual parameters
In my experience, you will mostly want to set priors for different "class"es of parameters, e.g.:
Intercept,b,sd,sigma,cor
Almost no difference in this case
m_brms2## Family: gaussian ## Links: mu = identity; sigma = identity ## Formula: popular ~ extrav + (extrav | class) ## Data: popular (Number of observations: 2000) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Group-Level Effects: ## ~class (Number of levels: 100) ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sd(Intercept) 1.70 0.17 1.39 2.06 1.01 1358 1824## sd(extrav) 0.16 0.03 0.11 0.22 1.00 871 1683## cor(Intercept,extrav) -0.95 0.03 -1.00 -0.88 1.01 437 871## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 2.48 0.20 2.08 2.86 1.00 1157 1810## extrav 0.49 0.03 0.44 0.54 1.00 1960 2642## ## Family Specific Parameters: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sigma 0.95 0.02 0.92 0.98 1.00 3976 2977## ## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).Installing cmdstan
First, install the {cmdstanr} package
install.packages( "cmdstanr", repos = c( "https://mc-stan.org/r-packages/", getOption("repos") ))Installing cmdstan
First, install the {cmdstanr} package
install.packages( "cmdstanr", repos = c( "https://mc-stan.org/r-packages/", getOption("repos") ))Then, install cmdstan
cmdstanr::install_cmdstan()Timings
I'm not evaluating the below, but the timings were 112.646, 84.561, and 42.934 seconds, respectively.
library(tictoc)tic()m_brms <- brm(popular ~ extrav + (extrav|class), data = popular)toc()# cmdstantic()m_brms2 <- brm(popular ~ extrav + (extrav|class), data = popular, backend = "cmdstanr")toc()# cmdstan w/parallelizationtic()m_brms3 <- brm(popular ~ extrav + (extrav|class), data = popular, backend = "cmdstanr", cores = 4)toc()Advantages to Bayes
Opportunity to incorporate prior knowledge into the modeling process (you don't really have to - could just set wide priors)
Natural interpretation of uncertainty
Can often allow you to estimate models that are difficult if not impossible with frequentist methods
Disadvatages
Generally going to be slower in implementation
You may run into pushback from others - particularly with respect to priors
Notes on the posterior
The posterior is the distribution of the parameters, given the data
Think of it as the distribution of what we don't know, but are interested in (model parameters), given what we know or have observed (the data), and our prior beliefs
Gives a complete picture of parameter uncertainty
We can do lots of things with the posterior that is hard to get otherwise
Data generating distribution
Up to this point, we've been assuming the data were generated from a normal distribution.
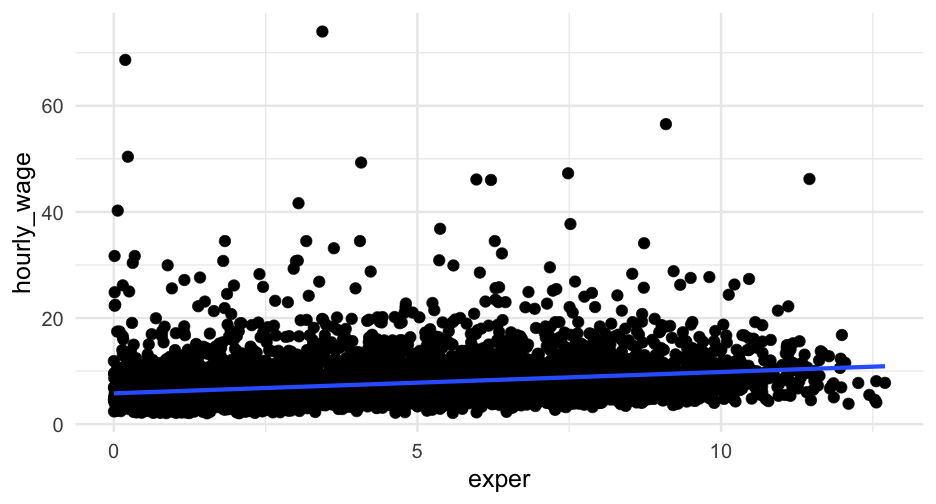
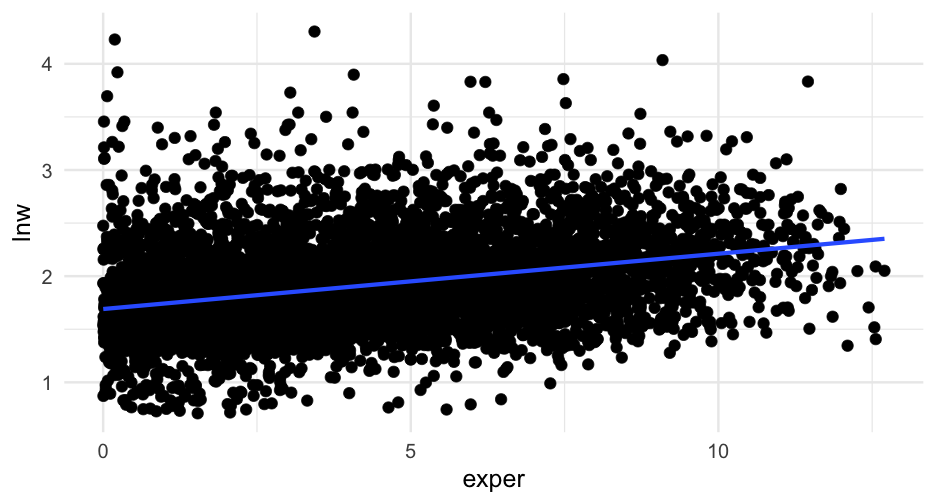
For example, we might fit a simple linear regression model to the wages data like this
wagesi∼N(ˆy,σ2)ˆy=α+β1(exper)
where we're embedding a linear model into the mean In code
wages <- read_csv(here::here("data", "wages.csv")) %>% mutate(hourly_wage = exp(lnw))wages_lm <- lm(hourly_wage ~ exper, data = wages)Move to binary model
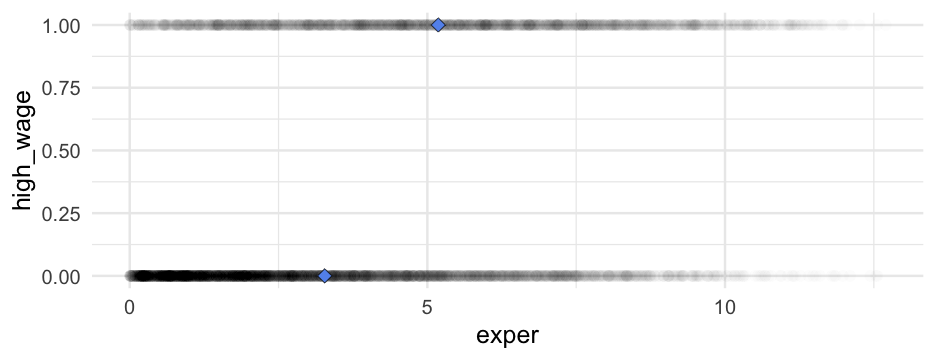
Let's split the wages data into a binary classification based on whether it's above or below the mean.
wages <- wages %>% mutate( high_wage = ifelse( hourly_wage > mean(hourly_wage, na.rm = TRUE), 1, 0 ) )wages %>% select(id, hourly_wage, high_wage)## # A tibble: 6,402 x 3## id hourly_wage high_wage## <dbl> <dbl> <dbl>## 1 31 4.441535 0## 2 31 4.191254 0## 3 31 4.344888 0## 4 31 5.748851 0## 5 31 6.896403 0## 6 31 5.523435 0## 7 31 8.052640 1## 8 31 8.406456 1## 9 36 7.257243 0## 10 36 6.037560 0## # … with 6,392 more rowsWe could fit a linear model
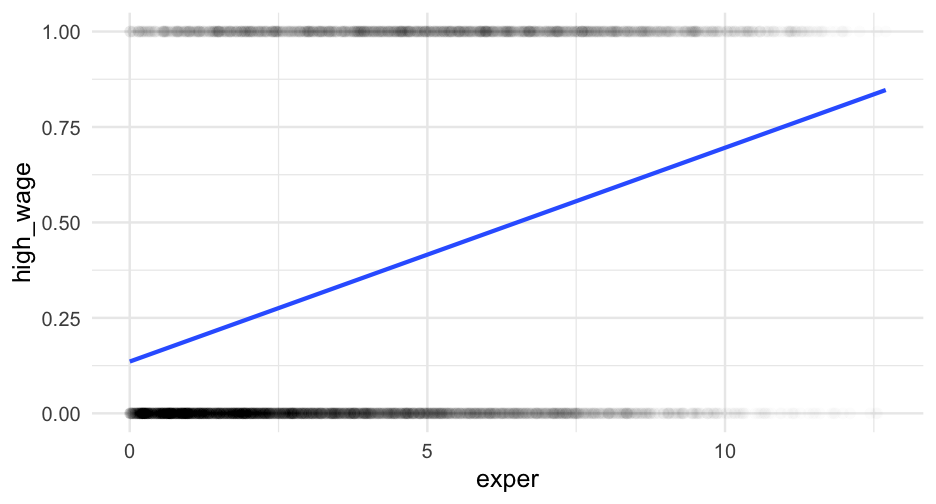
m_lpm <- lm(high_wage ~ exper, data = wages)arm::display(m_lpm)## lm(formula = high_wage ~ exper, data = wages)## coef.est coef.se## (Intercept) 0.14 0.01 ## exper 0.06 0.00 ## ---## n = 6402, k = 2## residual sd = 0.45, R-Squared = 0.11This is referred to as a linear probability model (LPM) and they are pretty hotly contested, with proponents and detractors
Prediction
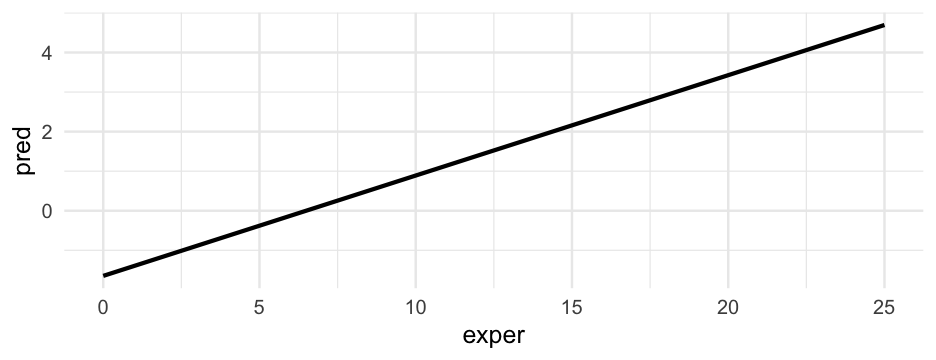
What if somebody has an experience of 25 years?
predict(m_lpm, newdata = data.frame(exper = 25))## 1 ## 1.535723🤨
Our prediction goes outside the range of our data.
As a rule, the assumed data generating process should match the boundaries of the data.
Of course, you could truncate after the fact. I think that's less than ideal (see here or here for discussions contrasting LPM with logistic regression).
Example
Flip 1 coin 10 times
set.seed(42)rbinom( n = 10, # number of trials size = 1, # number of coins prob = 0.5 # probability of heads)## [1] 1 1 0 1 1 1 1 0 1 1Side note - a binomial model with size = 1 (or n=1 in equation form) is equivalent to a Bernoulli distribution
Flip 10 coins 1 time
rbinom(n = 1, size = 10, prob = 0.5)## [1] 5Link functions
We solve this problem by using a link function
yi∼Binomial(n,pi)f(pi)=α+β(xi)
Instead of modeling pi directly, we model f(pi)
The specific f is the link function
Link functions map the linear space of the model to the non-linear parameters (like probability)
The log and logit links are most common
Example logistic regression model
m_glm <- glm(high_wage ~ exper, data = wages, family = binomial(link = "logit"))arm::display(m_glm)## glm(formula = high_wage ~ exper, family = binomial(link = "logit"), ## data = wages)## coef.est coef.se## (Intercept) -1.65 0.05 ## exper 0.25 0.01 ## ---## n = 6402, k = 2## residual deviance = 7655.2, null deviance = 8345.8 (difference = 690.5)Coefficient interpretation
The coefficients are reported on the log-odds scale. Other than that, interpretation is the same.
For example:
The log-odds of a participant with zero years experience being in the high wage category was -1.65.
For every one year of additional experience, the log-odds of being in the high wage category increased by 0.25.
Divide by 4
Logistic curve is steepest when pi=0.5
The slope of the logistic curve (its derivative) is maximized at β/4
Aside from the intercept, we can say that the change is no more than β/4
Example
0.254=0.0625 So, a one year increase in experience corresponds to, at most, a 6% increase in being in the high wage category
Example writeup
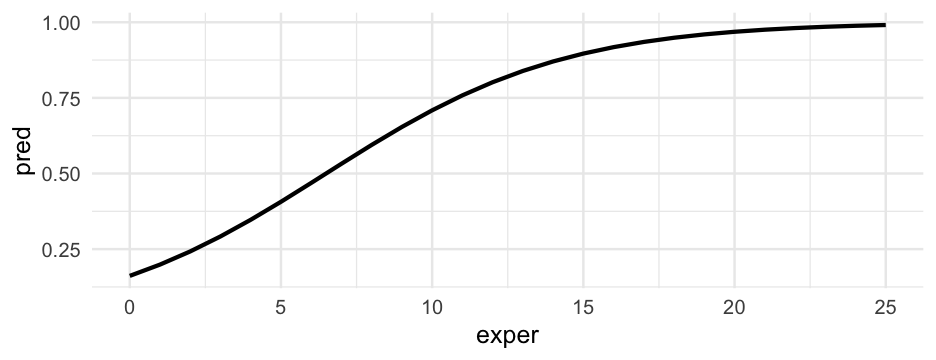
There was a 16 percent chance that a participant with zero years experience would be in the high wage category. The logistic function, which mapped years of experience to the probability of being in the high-wage category, was non-linear, as shown in Figure 1. At its steepest point, a one year increase in experience corresponded with approximately a 6% increase in the probability of being in the high-wage category. For individuals with 5, 10, and 15 years of experience, the probability increased to a 41, 71, and 90 percent chance, respectively.
The data
Polling data from the 1988 election.
polls <- rio::import(here::here("data", "polls.dta"), setclass = "tbl_df")polls## # A tibble: 13,544 x 10## org year survey bush state edu age female black weight## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 1 1 1 1 7 2 2 1 0 1403## 2 1 1 1 1 33 4 3 0 0 778## 3 1 1 1 0 20 2 1 1 0 1564## 4 1 1 1 1 31 3 2 1 0 1055## 5 1 1 1 1 18 3 1 1 0 1213## 6 1 1 1 1 31 4 2 0 0 910## 7 1 1 1 1 40 1 3 0 0 735## 8 1 1 1 1 33 4 2 1 0 410## 9 1 1 1 0 22 4 2 1 0 410## 10 1 1 1 1 22 4 3 0 0 778## # … with 13,534 more rowsIn code
Can you write the code for the previous model?
01:00
bush_sl <- glm(bush ~ 1, data = polls, family = binomial(link = "logit"))arm::display(bush_sl)## glm(formula = bush ~ 1, family = binomial(link = "logit"), data = polls)## coef.est coef.se## (Intercept) 0.25 0.02 ## ---## n = 11566, k = 1## residual deviance = 15858.1, null deviance = 15858.1 (difference = 0.0)In code
Can you write the code for the previous model?
01:00
bush_sl <- glm(bush ~ 1, data = polls, family = binomial(link = "logit"))arm::display(bush_sl)## glm(formula = bush ~ 1, family = binomial(link = "logit"), data = polls)## coef.est coef.se## (Intercept) 0.25 0.02 ## ---## n = 11566, k = 1## residual deviance = 15858.1, null deviance = 15858.1 (difference = 0.0)So, pi=exp(0.25)1+exp(0.25)=0.56
State-level variability
To estimate state-level variability, we just specify a distribution for the intercept variability.
bush∼Binomial(n=1,probbush=1=^P)log[^P1−^P]=αj[i]αj∼N(μαj,σ2αj), for state j = 1,…,J Notice we're still specifying that the intercept variability is generated by a normal distribution.
State-level variability
To estimate state-level variability, we just specify a distribution for the intercept variability.
bush∼Binomial(n=1,probbush=1=^P)log[^P1−^P]=αj[i]αj∼N(μαj,σ2αj), for state j = 1,…,J Notice we're still specifying that the intercept variability is generated by a normal distribution.
What does this variability actually represent?
State-level variability
To estimate state-level variability, we just specify a distribution for the intercept variability.
bush∼Binomial(n=1,probbush=1=^P)log[^P1−^P]=αj[i]αj∼N(μαj,σ2αj), for state j = 1,…,J Notice we're still specifying that the intercept variability is generated by a normal distribution.
What does this variability actually represent?
Variance in the log-odds
Fitting the model
If we're using {lme4}, we just swap lmer() for glmer() and specify the family and link function.
library(lme4)m0 <- glmer(bush ~ 1 + (1|state), data = polls, family = binomial(link = "logit"))arm::display(m0)## glmer(formula = bush ~ 1 + (1 | state), data = polls, family = binomial(link = "logit"))## coef.est coef.se ## 0.25 0.06 ## ## Error terms:## Groups Name Std.Dev.## state (Intercept) 0.34 ## Residual 1.00 ## ---## number of obs: 11566, groups: state, 49## AIC = 15697, DIC = 15450.4## deviance = 15571.7State-level variation
library(broom.mixed)m0_tidied <- tidy(m0, effects = "ran_vals", conf.int = TRUE)m0_tidied## # A tibble: 49 x 8## effect group level term estimate std.error conf.low conf.high## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl>## 1 ran_vals state 1 (Intercept) 0.5201836 0.1526301 0.2210341 0.8193332 ## 2 ran_vals state 3 (Intercept) 0.09438107 0.1424292 -0.1847750 0.3735371 ## 3 ran_vals state 4 (Intercept) 0.06905650 0.1737493 -0.2714859 0.4095989 ## 4 ran_vals state 5 (Intercept) 0.03522421 0.05570977 -0.07396493 0.1444133 ## 5 ran_vals state 6 (Intercept) 0.1045418 0.1513626 -0.1921233 0.4012070 ## 6 ran_vals state 7 (Intercept) -0.1015410 0.1546380 -0.4046260 0.2015440 ## 7 ran_vals state 8 (Intercept) -0.3824312 0.2376744 -0.8482644 0.08340195## 8 ran_vals state 9 (Intercept) -0.6229779 0.2931982 -1.197636 -0.04832002## 9 ran_vals state 10 (Intercept) 0.3027001 0.07975137 0.1463903 0.4590099 ## 10 ran_vals state 11 (Intercept) 0.09282107 0.1173420 -0.1371651 0.3228072 ## # … with 39 more rowsFancified Plot Code
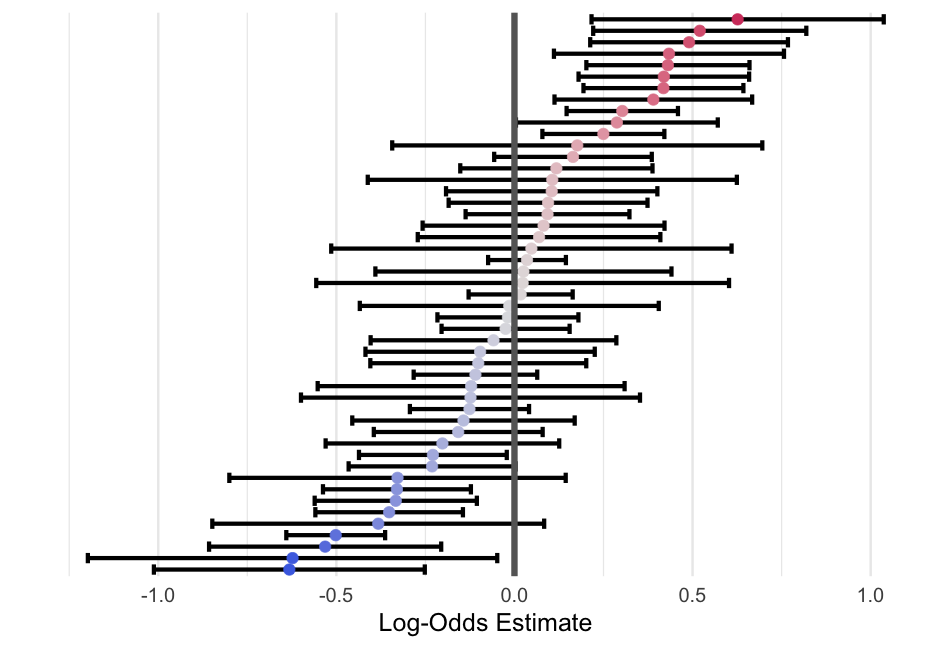
m0_tidied %>% mutate(level = forcats::fct_reorder(level, estimate)) %>% ggplot(aes(estimate, level)) + geom_errorbarh(aes(xmin = conf.low, xmax = conf.high)) + geom_point(aes(color = estimate)) + geom_vline(xintercept = 0, color = "gray40", size = 3) + labs(x = "Log-Odds Estimate", y = "") + colorspace::scale_color_continuous_diverging(palette = "Blue-Red 2") + guides(color = "none") + theme(panel.grid.major.y = element_blank(), axis.text.y = element_blank())polls <- polls %>% mutate(age_c = age - mean(age, na.rm = TRUE))m1 <- glmer(bush ~ age_c + female + black + (1|state), data = polls, family = binomial(link = "logit"))arm::display(m1)## glmer(formula = bush ~ age_c + female + black + (1 | state), ## data = polls, family = binomial(link = "logit"))## coef.est coef.se## (Intercept) 0.43 0.07 ## age_c -0.08 0.02 ## female -0.11 0.04 ## black -1.84 0.09 ## ## Error terms:## Groups Name Std.Dev.## state (Intercept) 0.41 ## Residual 1.00 ## ---## number of obs: 11566, groups: state, 49## AIC = 15137.1, DIC = 14856.7## deviance = 14991.9Varying slopes
The average probability of a respondent who was coded black == 1 who was the average age and non-female supporting Bush was
(pi|age=0,female=0,black=1)=exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1))1+exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1)) (pi|age=0,female=0,black=1)=exp(0.43−1.84))1+exp(0.43−1.84)
Varying slopes
The average probability of a respondent who was coded black == 1 who was the average age and non-female supporting Bush was
(pi|age=0,female=0,black=1)=exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1))1+exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1)) (pi|age=0,female=0,black=1)=exp(0.43−1.84))1+exp(0.43−1.84) (pi|age=0,female=0,black=1)=exp(−1.41))1+exp(−1.41)
Varying slopes
The average probability of a respondent who was coded black == 1 who was the average age and non-female supporting Bush was
(pi|age=0,female=0,black=1)=exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1))1+exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1)) (pi|age=0,female=0,black=1)=exp(0.43−1.84))1+exp(0.43−1.84) (pi|age=0,female=0,black=1)=exp(−1.41))1+exp(−1.41) (pi|age=0,female=0,black=1)=0.241.24
Varying slopes
The average probability of a respondent who was coded black == 1 who was the average age and non-female supporting Bush was
(pi|age=0,female=0,black=1)=exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1))1+exp(0.43+(−0.08×0)+(−0.11×0)+(−1.84×1)) (pi|age=0,female=0,black=1)=exp(0.43−1.84))1+exp(0.43−1.84) (pi|age=0,female=0,black=1)=exp(−1.41))1+exp(−1.41) (pi|age=0,female=0,black=1)=0.241.24 (pi|age=0,female=0,black=1)=0.19
Vary by state?
You try first - try to fit a model that estimates between-state variability in the relation between individuals coded black, and their probability of voting for Bush.
01:00
m2 <- glmer(bush ~ age_c + female + black + (black|state), data = polls, family = binomial(link = "logit"))arm::display(m2)## glmer(formula = bush ~ age_c + female + black + (black | state), ## data = polls, family = binomial(link = "logit"))## coef.est coef.se## (Intercept) 0.43 0.07 ## age_c -0.08 0.02 ## female -0.11 0.04 ## black -1.66 0.19 ## ## Error terms:## Groups Name Std.Dev. Corr ## state (Intercept) 0.44 ## black 0.87 -0.46 ## Residual 1.00 ## ---## number of obs: 11566, groups: state, 49## AIC = 15100.6, DIC = 14697.4## deviance = 14892.0Look at random effects
ranef_m2 <- tidy(m2, effects = "ran_vals", conf.int = TRUE) %>% arrange(level)ranef_m2## # A tibble: 98 x 8## effect group level term estimate std.error conf.low conf.high## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl>## 1 ran_vals state 1 (Intercept) 0.4768807 0.1716175 0.1405165 0.8132448## 2 ran_vals state 1 black 1.066314 0.4118905 0.2590240 1.873605 ## 3 ran_vals state 10 (Intercept) 0.3000900 0.08425460 0.1349540 0.4652259## 4 ran_vals state 10 black -0.1573061 0.3564817 -0.8559974 0.5413852## 5 ran_vals state 11 (Intercept) 0.2440973 0.1326607 -0.01591285 0.5041074## 6 ran_vals state 11 black -0.6672948 0.4129706 -1.476702 0.1421127## 7 ran_vals state 13 (Intercept) -0.2406066 0.2710096 -0.7717756 0.2905624## 8 ran_vals state 13 black 0.2180487 0.8103377 -1.370184 1.806281 ## 9 ran_vals state 14 (Intercept) -0.04190335 0.09568848 -0.2294493 0.1456426## 10 ran_vals state 14 black -0.3926602 0.3611247 -1.100452 0.3151311## # … with 88 more rowsInclude fixed effects
fe <- data.frame( fixed = fixef(m2), term = names(fixef(m2)))fe## fixed term## (Intercept) 0.43434106 (Intercept)## age_c -0.08284379 age_c## female -0.10836146 female## black -1.66095113 blackranef_m2 <- left_join(ranef_m2, fe)ranef_m2 %>% select(level, term, estimate, fixed)## # A tibble: 98 x 4## level term estimate fixed## <chr> <chr> <dbl> <dbl>## 1 1 (Intercept) 0.4768807 0.4343411## 2 1 black 1.066314 -1.660951 ## 3 10 (Intercept) 0.3000900 0.4343411## 4 10 black -0.1573061 -1.660951 ## 5 11 (Intercept) 0.2440973 0.4343411## 6 11 black -0.6672948 -1.660951 ## 7 13 (Intercept) -0.2406066 0.4343411## 8 13 black 0.2180487 -1.660951 ## 9 14 (Intercept) -0.04190335 0.4343411## 10 14 black -0.3926602 -1.660951 ## # … with 88 more rowsAdd in fixed effects
ranef_m2 <- ranef_m2 %>% mutate(estimate = estimate + fixed)ranef_m2## # A tibble: 98 x 9## effect group level term estimate std.error conf.low conf.high fixed## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 ran_vals state 1 (Intercept) 0.9112217 0.1716175 0.1405165 0.8132448 0.4343411## 2 ran_vals state 1 black -0.5946367 0.4118905 0.2590240 1.873605 -1.660951 ## 3 ran_vals state 10 (Intercept) 0.7344310 0.08425460 0.1349540 0.4652259 0.4343411## 4 ran_vals state 10 black -1.818257 0.3564817 -0.8559974 0.5413852 -1.660951 ## 5 ran_vals state 11 (Intercept) 0.6784383 0.1326607 -0.01591285 0.5041074 0.4343411## 6 ran_vals state 11 black -2.328246 0.4129706 -1.476702 0.1421127 -1.660951 ## 7 ran_vals state 13 (Intercept) 0.1937344 0.2710096 -0.7717756 0.2905624 0.4343411## 8 ran_vals state 13 black -1.442902 0.8103377 -1.370184 1.806281 -1.660951 ## 9 ran_vals state 14 (Intercept) 0.3924377 0.09568848 -0.2294493 0.1456426 0.4343411## 10 ran_vals state 14 black -2.053611 0.3611247 -1.100452 0.3151311 -1.660951 ## # … with 88 more rowsCompute log-odds
Compute means for each group - i.e., add the coefficients
to_plot <- ranef_m2 %>% group_by(level) %>% mutate(estimate = cumsum(estimate)) %>% ungroup()to_plot## # A tibble: 98 x 9## effect group level term estimate std.error conf.low conf.high fixed## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 ran_vals state 1 (Intercept) 0.9112217 0.1716175 0.1405165 0.8132448 0.4343411## 2 ran_vals state 1 black 0.3165850 0.4118905 0.2590240 1.873605 -1.660951 ## 3 ran_vals state 10 (Intercept) 0.7344310 0.08425460 0.1349540 0.4652259 0.4343411## 4 ran_vals state 10 black -1.083826 0.3564817 -0.8559974 0.5413852 -1.660951 ## 5 ran_vals state 11 (Intercept) 0.6784383 0.1326607 -0.01591285 0.5041074 0.4343411## 6 ran_vals state 11 black -1.649808 0.4129706 -1.476702 0.1421127 -1.660951 ## 7 ran_vals state 13 (Intercept) 0.1937344 0.2710096 -0.7717756 0.2905624 0.4343411## 8 ran_vals state 13 black -1.249168 0.8103377 -1.370184 1.806281 -1.660951 ## 9 ran_vals state 14 (Intercept) 0.3924377 0.09568848 -0.2294493 0.1456426 0.4343411## 10 ran_vals state 14 black -1.661174 0.3611247 -1.100452 0.3151311 -1.660951 ## # … with 88 more rowsPlot
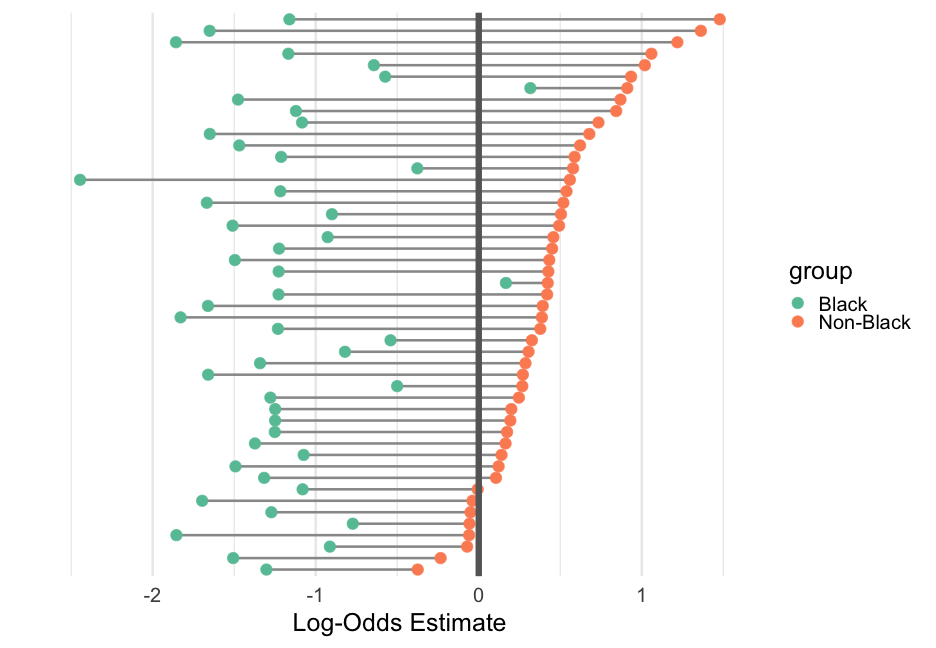
# data transformto_plot %>% mutate(group = ifelse(term == "(Intercept)", "Non-Black", "Black")) %>% # plot ggplot(aes(estimate, level)) + geom_line(aes(group = level), color = "gray60", size = 1.2) + geom_point(aes(color = group)) + geom_vline(xintercept = 0.5, color = "gray40", size = 3) + # themeing stuff labs(x = "Probability Estimate", y = "") + xlim(0, 1) + scale_color_brewer(palette = "Set2") + theme(panel.grid.major.y = element_blank(), axis.text.y = element_blank())Probability scale
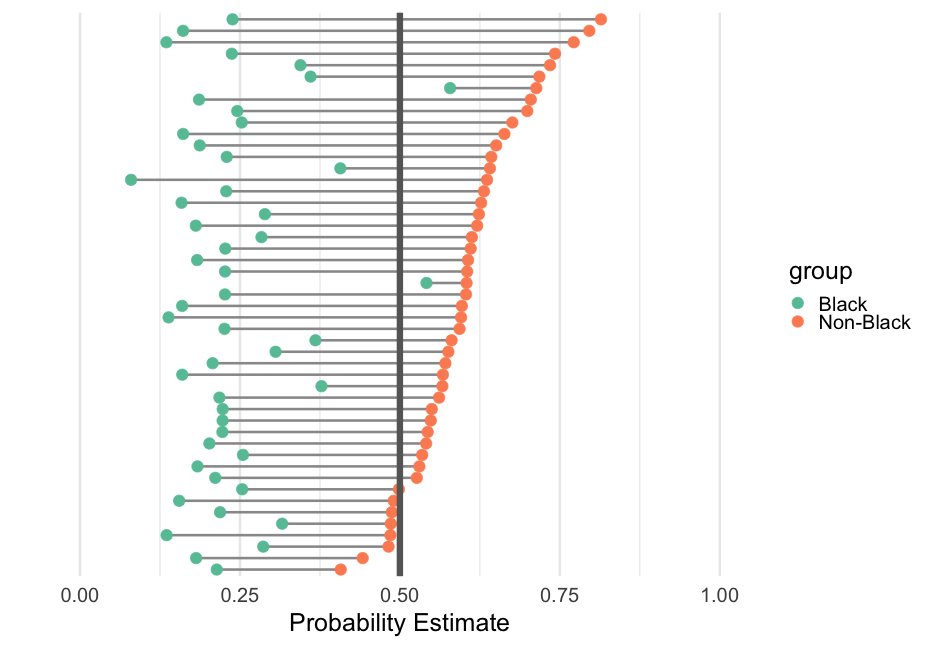
# data transformto_plot %>% mutate( group = ifelse(term == "(Intercept)", "Non-Black", "Black"), prob = exp(estimate)/(1 + exp(estimate)) ) %>% # plot ggplot(aes(prob, level)) + geom_line(aes(group = level), color = "gray60", size = 1.2) + geom_point(aes(color = group)) + geom_vline(xintercept = 0.5, color = "gray40", size = 3) + # themeing stuff labs(x = "Probability Estimate", y = "") + xlim(0, 1) + scale_color_brewer(palette = "Set2") + theme(panel.grid.major.y = element_blank(), axis.text.y = element_blank())Flat priors
library(brms)m2_brms <- brm(bush ~ age + female + black + (black|state), data = polls, family = bernoulli(link = "logit"), backend = "cmdstan", cores = 4)## Warning: Rows containing NAs were excluded from the model.## -\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-\|/-Running MCMC with 4 parallel chains...## ## Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup) ## Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup) ## Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup) ## Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup) ## Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup) ## Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup) ## Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup) ## Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup) ## Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup) ## Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup) ## Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup) ## Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup) ## Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup) ## Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup) ## Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup) ## Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup) ## Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup) ## Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup) ## Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup) ## Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup) ## Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup) ## Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup) ## Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup) ## Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup) ## Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup) ## Chain 4 Iteration: 600 / 2000 [ 30%] (Warmup) ## Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup) ## Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup) ## Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup) ## Chain 4 Iteration: 700 / 2000 [ 35%] (Warmup) ## Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup) ## Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup) ## Chain 3 Iteration: 700 / 2000 [ 35%] (Warmup) ## Chain 4 Iteration: 800 / 2000 [ 40%] (Warmup) ## Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup) ## Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup) ## Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup) ## Chain 4 Iteration: 900 / 2000 [ 45%] (Warmup) ## Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup) ## Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling) ## Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup) ## Chain 3 Iteration: 900 / 2000 [ 45%] (Warmup) ## Chain 4 Iteration: 1000 / 2000 [ 50%] (Warmup) ## Chain 4 Iteration: 1001 / 2000 [ 50%] (Sampling) ## Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling) ## Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup) ## Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling) ## Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling) ## Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup) ## Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling) ## Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling) ## Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling) ## Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling) ## Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling) ## Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling) ## Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling) ## Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling) ## Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling) ## Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling) ## Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling) ## Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling) ## Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling) ## Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling) ## Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling) ## Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling) ## Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling) ## Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling) ## Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling) ## Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling) ## Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling) ## Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling) ## Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling) ## Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling) ## Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling) ## Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling) ## Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling) ## Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling) ## Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling) ## Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling) ## Chain 2 Iteration: 2000 / 2000 [100%] (Sampling) ## Chain 2 finished in 41.0 seconds.## Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling) ## Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling) ## Chain 4 Iteration: 2000 / 2000 [100%] (Sampling) ## Chain 4 finished in 41.9 seconds.## Chain 1 Iteration: 2000 / 2000 [100%] (Sampling) ## Chain 1 finished in 42.7 seconds.## Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling) ## Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling) ## Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling) ## Chain 3 Iteration: 2000 / 2000 [100%] (Sampling) ## Chain 3 finished in 48.2 seconds.## ## All 4 chains finished successfully.## Mean chain execution time: 43.5 seconds.## Total execution time: 48.7 seconds.Model summary
summary(m2_brms)## Family: bernoulli ## Links: mu = logit ## Formula: bush ~ age + female + black + (black | state) ## Data: polls (Number of observations: 11566) ## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;## total post-warmup samples = 4000## ## Group-Level Effects: ## ~state (Number of levels: 49) ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## sd(Intercept) 0.46 0.06 0.36 0.59 1.00 949 2013## sd(black) 0.96 0.20 0.61 1.41 1.01 1202 2403## cor(Intercept,black) -0.40 0.19 -0.71 0.02 1.00 1417 2354## ## Population-Level Effects: ## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS## Intercept 0.62 0.09 0.46 0.80 1.00 732 1254## age -0.08 0.02 -0.12 -0.05 1.00 5674 3257## female -0.11 0.04 -0.19 -0.03 1.00 5243 2793## black -1.67 0.22 -2.10 -1.24 1.00 1050 1688## ## Samples were drawn using sample(hmc). For each parameter, Bulk_ESS## and Tail_ESS are effective sample size measures, and Rhat is the potential## scale reduction factor on split chains (at convergence, Rhat = 1).