More Bayes

class: center, middle, inverse, title-slide

# More Bayes
## And multilevel binomial logistic regression
### Daniel Anderson
### Week 8

---

layout: true

---
# Agenda
* More equation practice

* Finishing up our intro to Bayes
  + Specific focus on MCMC

* Implementation with **{brms}**

* Logistic regression review

* Extending to multilevel logistic regression models with **lme4**

---
class: inverse-blue middle
# Equation practice

---
# The data
Read in the following data

```r
library(tidyverse)
library(lme4)
d <- read_csv(here::here("data", "three-lev.csv"))
d
```

```
## # A tibble: 7,230 x 12
##    schid       sid  size lowinc mobility female black hispanic retained grade  year   math
##    <dbl>     <dbl> <dbl>  <dbl>    <dbl>  <dbl> <dbl>    <dbl>    <dbl> <dbl> <dbl>  <dbl>
##  1  2020 273026452   380   40.3     12.5      0     0        1        0     2   0.5  1.146
##  2  2020 273026452   380   40.3     12.5      0     0        1        0     3   1.5  1.134
##  3  2020 273026452   380   40.3     12.5      0     0        1        0     4   2.5  2.3  
##  4  2020 273030991   380   40.3     12.5      0     0        0        0     0  -1.5 -1.303
##  5  2020 273030991   380   40.3     12.5      0     0        0        0     1  -0.5  0.439
##  6  2020 273030991   380   40.3     12.5      0     0        0        0     2   0.5  2.43 
##  7  2020 273030991   380   40.3     12.5      0     0        0        0     3   1.5  2.254
##  8  2020 273030991   380   40.3     12.5      0     0        0        0     4   2.5  3.873
##  9  2020 273059461   380   40.3     12.5      0     0        1        0     0  -1.5 -1.384
## 10  2020 273059461   380   40.3     12.5      0     0        1        0     1  -0.5  0.338
## # … with 7,220 more rows
```

---
# Model 1

Fit the following model

$$
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i]}, \sigma^2 \right) \\
    \alpha_{j}  &\sim N \left(\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{mobility}), \sigma^2_{\alpha_{j}} \right)
    \text{, for schid j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(math ~ mobility + (1|schid), data = d)
```

---
# Model 2

Fit the following model

$$
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{female}) \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    \alpha_{k}  &\sim N \left(\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{mobility}), \sigma^2_{\alpha_{k}} \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year + female + mobility + 
             (year|sid) +  (1|schid), 
     data = d)
```

---
# Model 3

Fit the following model

$$
\small
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{black}) + \gamma_{2}^{\alpha}(\operatorname{hispanic}) + \gamma_{3}^{\alpha}(\operatorname{female}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{black}) + \gamma^{\beta_{1}}_{2}(\operatorname{hispanic})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    \alpha_{k}  &\sim N \left(\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{mobility}), \sigma^2_{\alpha_{k}} \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year * black + year * hispanic + female + mobility + 
             (year|sid) +  (1|schid), 
     data = d)
```

---
# Model 4

Fit the following model

$$
\small
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1k[i]}^{\alpha}(\operatorname{female}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{female})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\gamma_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{mobility}) + \gamma_{2}^{\alpha}(\operatorname{lowinc}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{mobility}) \\
      &\mu_{\gamma_{1k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{ccc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} & \rho_{\alpha_{k}\gamma_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}} & \rho_{\beta_{1k}\gamma_{1k}} \\ 
     \rho_{\gamma_{1k}\alpha_{k}} & \rho_{\gamma_{1k}\beta_{1k}} & \sigma^2_{\gamma_{1k}}
  \end{array}
\right)
 \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year * female + year * mobility + lowinc +
             (year|sid) +  (year + female|schid), 
     data = d)
```

---
# Model 5

Fit the following model

Don't worry if you run into convergene warnings

$$
\scriptsize
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1k[i]}^{\alpha}(\operatorname{female}) \\
      &\gamma^{\beta_{1}}_{1k[i0} + \gamma^{\beta_{1}}_{1k[i]}(\operatorname{female})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k} \\
      &\gamma_{1k} \\
      &\gamma^{\beta_{1}}_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{mobility}) + \gamma_{2}^{\alpha}(\operatorname{lowinc}) \\
      &\mu_{\beta_{1k}} \\
      &\mu_{\gamma_{1k}} \\
      &\mu_{\gamma^{\beta_{1}}_{1k}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cccc}
     \sigma^2_{\alpha_{k}} & 0 & 0 & 0 \\ 
     0 & \sigma^2_{\beta_{1k}} & 0 & 0 \\ 
     0 & 0 & \sigma^2_{\gamma_{1k}} & 0 \\ 
     0 & 0 & 0 & \sigma^2_{\gamma^{\beta_{1}}_{1k}}
  \end{array}
\right)
 \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year * female + mobility + lowinc +
       (year|sid) +  (year * female||schid), 
     data = d)
```

---
# Model 6

Fit the following model

$$
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{female}) \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    \gamma_{1k}  &\sim N \left(\mu_{\gamma_{1k}}, \sigma^2_{\gamma_{1k}} \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year + female + mobility * size +
             (year|sid) +  (0 + mobility|schid), 
     data = d)
```

---
# Model 7

Fit the following model

$$
\scriptsize
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{female}) + \gamma_{2}^{\alpha}(\operatorname{mobility}) + \gamma_{3}^{\alpha}(\operatorname{size}) \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J}
\end{aligned}`
$$

```r
lmer(math ~ year + female + mobility + size +
       (year|sid), 
     data = d)
```

---
# Model 8

Last one

$$
\scriptsize
`\begin{aligned}
  \operatorname{math}_{i}  &\sim N \left(\alpha_{j[i],k[i]} + \beta_{1j[i],k[i]}(\operatorname{year}), \sigma^2 \right) \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{j} \\
      &\beta_{1j}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{female}) \\
      &\mu_{\beta_{1j}}
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ 
     \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}}
  \end{array}
\right)
 \right)
    \text{, for sid j = 1,} \dots \text{,J} \\    
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\alpha_{k} \\
      &\beta_{1k}
    \end{aligned}
  \end{array}
\right)
  &\sim N \left(
\left(
  \begin{array}{c} 
    \begin{aligned}
      &\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{lowinc}) \\
      &\gamma^{\beta_{1}}_{0} + \gamma^{\beta_{1}}_{1}(\operatorname{lowinc})
    \end{aligned}
  \end{array}
\right)
, 
\left(
  \begin{array}{cc}
     \sigma^2_{\alpha_{k}} & \rho_{\alpha_{k}\beta_{1k}} \\ 
     \rho_{\beta_{1k}\alpha_{k}} & \sigma^2_{\beta_{1k}}
  \end{array}
\right)
 \right)
    \text{, for schid k = 1,} \dots \text{,K}
\end{aligned}`
$$

```r
lmer(math ~ year * lowinc + female + 
       (year|sid) + (year |schid), 
     data = d)
```

---
class: inverse-blue middle
# Finishing up w/Bayes intro

---
# Updated beliefs
* Remember our posterior is defined by

$$
\text{posterior} = \frac{ \text{likelihood} \times \text{prior}}{\text{average likelihood}}
$$

--
When we just had a single parameter to estimate, `$\mu$`, this was tractable with grid search.

--
With even simple linear regression, however, we have three parameters: `$\alpha$`, `$\beta$`, and `$\sigma$`

--
Our Bayesian model then becomes considerably more complicated:

$$
P(\alpha, \beta, \sigma \mid x) = \frac{ P(x \mid \alpha, \beta, \sigma) \, P(\alpha, \beta, \sigma)}{\iiint \, P(x \mid \alpha, \beta, \sigma) \, P(\alpha, \beta, \sigma) \,d\alpha \,d\beta \,d\sigma}
$$

---
# Estimation
Rather than trying to compute the integrals, we draw *samples* from the joint posterior distribution.

--
This sounds a bit like magic - how do we do this?

--
Multiple different algorithms, but all use some form of Markov-Chain Monte-Carlo sampling

---
# Conceptually

* Imagine the posterior as a hill

* We start with the parameters set to random numbers

+ Estimate the posterior with this values (our spot on the hill)

* Try to "walk" around in a way that we get a complete "picture" of the hill from the samples

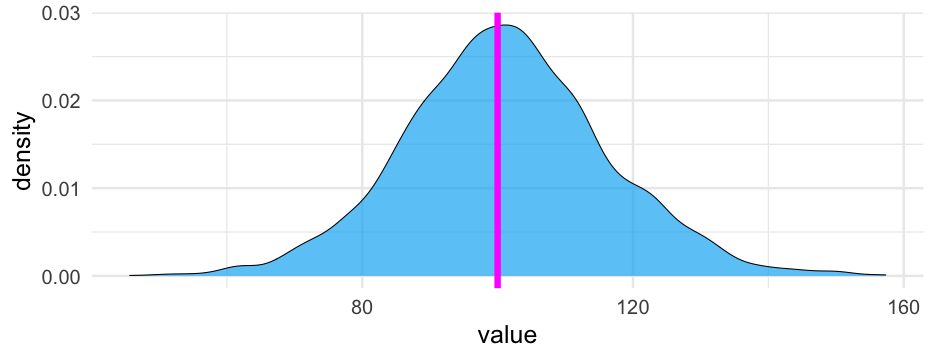
* Use these samples as your posterior distribution

---
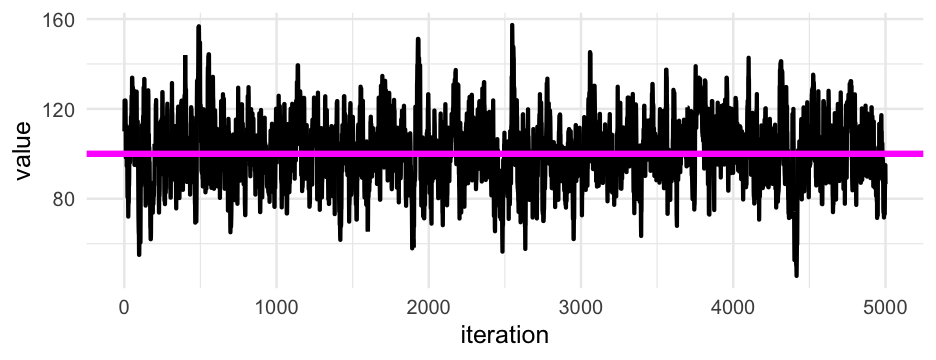
# An example

.footnote[Example from [Ravenzwaaij et al.](https://link.springer.com/article/10.3758/s13423-016-1015-8)]

Let's go back to an example where we're trying to estimate the mean with a know standard deviation.

--
$$
N(\mu, 15)
$$

--
Start with an initial guess, say 110

---
# MCMC
One algorithm:

* Generate a *proposal* by taking a sample from your best guess according to some distribution, e.g., `$\text{proposal} \sim N(110, 10)$`. Suppose we get a value of 108

--
* Observe the actual data. Let's say we have only one point: 100

* Compare the "height" of the proposal distribution to height of the current distribution, relative to observed data: `$N(100|110, 15)$`, `$N(100|108, 15)$`

---
# In code

```r
dnorm(110, 100, 15)
```

```
## [1] 0.02129653
```

```r
dnorm(108, 100, 15)
```

```
## [1] 0.02307026
```

---
* If probability of target distribution is higher, accept

* If probability  is lower, randomly select between the two with probability equal to the "heights" (probability of the two distributions)

* If proposal is accepted - it's the next sample in the chain

* Otherwise, the next sample is a copy of current sample

--
## This completes one iteration

Next iteration starts by generating a new proposal distribution

--
Stop when you have enough samples to have an adequate "picture"

---
# Example in code
Let's take 5000 samples

```r
set.seed(42) # for reproducibility

samples <- c(
  110, # initial guess
  rep(NA, 4999) # space for subsequent samples to fill in
)
```

---
# Loop

```r
for(i in 2:5000) {
  # generate proposal distribution
  proposal <- rnorm(1, mean = samples[i - 1], sd = 10)
  
  # calculate current/proposal distribution likelihoood
  prob_current <- dnorm(samples[i - 1], 100, 15)
  prob_proposal <- dnorm(proposal, 100, 15)
  
  # compute the probability ratio
  prob_ratio <- prob_proposal / prob_current
  
  # Determine which to select
  if(prob_ratio > runif(1)) {
    samples[i] <- proposal # accept
  } else {
    samples[i] <- samples[i - 1] # reject
  }
}
```

---
# Plot
Iteration history

```r
tibble(iteration = 1:5000,
       value = samples) %>% 
  ggplot(aes(iteration, value)) +
  geom_line() +
  geom_hline(yintercept = 100, 
             color = "magenta",
             size = 3)
```

![](w8p1_files/figure-html/unnamed-chunk-22-1.png)

---
# Plot
Density

```r
tibble(iteration = 1:5000,
       value = samples) %>% 
  ggplot(aes(value)) +
  geom_density(fill = "#00b4f5",
               alpha = 0.7) +
  geom_vline(xintercept = 100, 
             color = "magenta",
             size = 3)
```

![](w8p1_files/figure-html/unnamed-chunk-23-1.png)

---
class: inverse-red middle
# Bayes Update Script
Last week I promised a script to let you play around with priors. I'll show that now ("bayes-update-plotting.R")

There's also a MH script I'll quickly show.

### [demo]

---
class: inverse-blue middle

# Implementation with {brms}

Luckily, we don't have to program the MCMC algorithm ourselves

.center[
![](https://github.com/paul-buerkner/brms/raw/master/man/figures/brms.png)
]

---
# What is it?
* **b**ayesian **r**egression **m**odeling with **s**tan

* Uses [stan](https://mc-stan.org/) as the model backend - basically writes the model code for you then sends it to stan

* Allows model syntax similar to **lme4**

* Simple specification of priors - defaults are flat

* Provides many methods for post-model fitting inference

---
# Fit a basic model
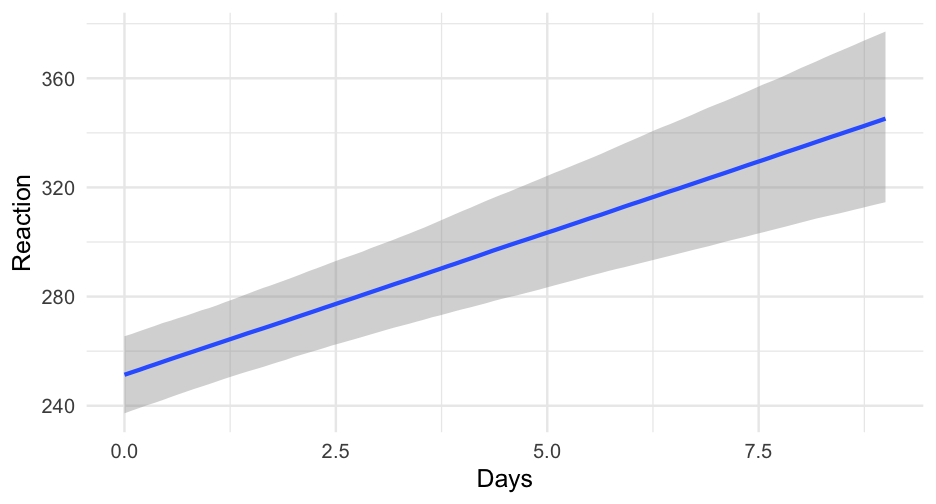
Let's start with the default (uninformative) priors, and fit a standard, simple-linear regression model

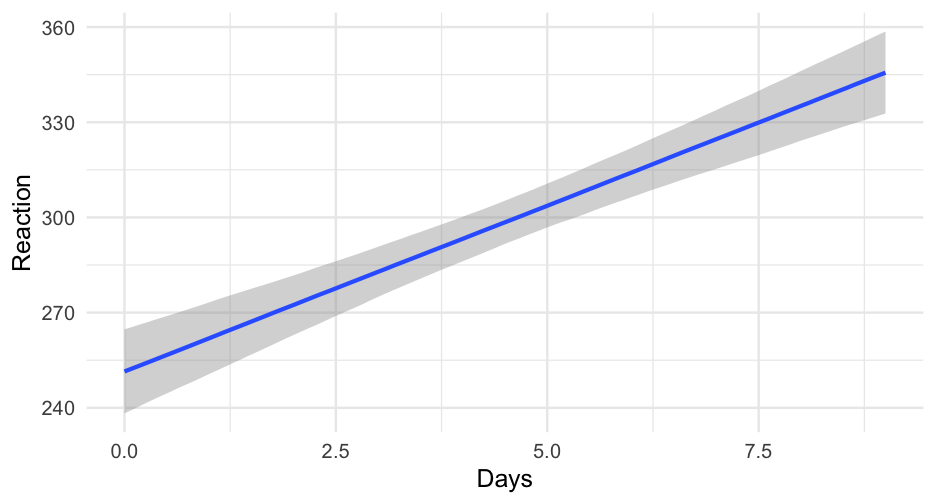
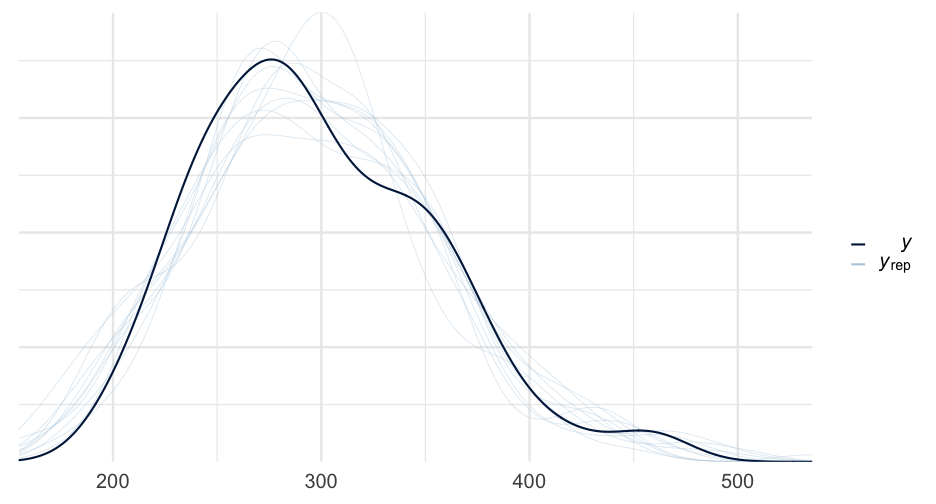
```r
library(brms)
sleep_m0 <- brm(Reaction ~ Days, data = lme4::sleepstudy)
```

```
## 
## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 1).
## Chain 1: 
## Chain 1: Gradient evaluation took 2.2e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.22 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1: 
## Chain 1: 
## Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 1: 
## Chain 1:  Elapsed Time: 0.050609 seconds (Warm-up)
## Chain 1:                0.017419 seconds (Sampling)
## Chain 1:                0.068028 seconds (Total)
## Chain 1: 
## 
## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 2).
## Chain 2: 
## Chain 2: Gradient evaluation took 6e-06 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2: 
## Chain 2: 
## Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 2: 
## Chain 2:  Elapsed Time: 0.048009 seconds (Warm-up)
## Chain 2:                0.021626 seconds (Sampling)
## Chain 2:                0.069635 seconds (Total)
## Chain 2: 
## 
## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 3).
## Chain 3: 
## Chain 3: Gradient evaluation took 1.2e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3: 
## Chain 3: 
## Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 3: 
## Chain 3:  Elapsed Time: 0.041524 seconds (Warm-up)
## Chain 3:                0.020323 seconds (Sampling)
## Chain 3:                0.061847 seconds (Total)
## Chain 3: 
## 
## SAMPLING FOR MODEL 'a3c55247ada09ee979052a314fc29ad7' NOW (CHAIN 4).
## Chain 4: 
## Chain 4: Gradient evaluation took 7e-06 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4: 
## Chain 4: 
## Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 4: 
## Chain 4:  Elapsed Time: 0.048884 seconds (Warm-up)
## Chain 4:                0.020719 seconds (Sampling)
## Chain 4:                0.069603 seconds (Total)
## Chain 4:
```

---
# Model summary

```r
summary(sleep_m0)
```

```
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: Reaction ~ Days 
##    Data: lme4::sleepstudy (Number of observations: 180) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept   251.49      6.64   238.26   264.74 1.00     4168     3040
## Days         10.45      1.25     7.98    12.90 1.00     4155     2967
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma    47.96      2.51    43.34    53.22 1.00     4069     2959
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# View "fixed" effect
Let's look at our estimated relation between `Days` and `Reaction`

```r
conditional_effects(sleep_m0)
```

![](w8p1_files/figure-html/unnamed-chunk-26-1.png)

---
# Wrong model
Of course, this is the wrong model, we have a multilevel structure

![](w8p1_files/figure-html/unnamed-chunk-27-1.png)

---
# Multilevel model
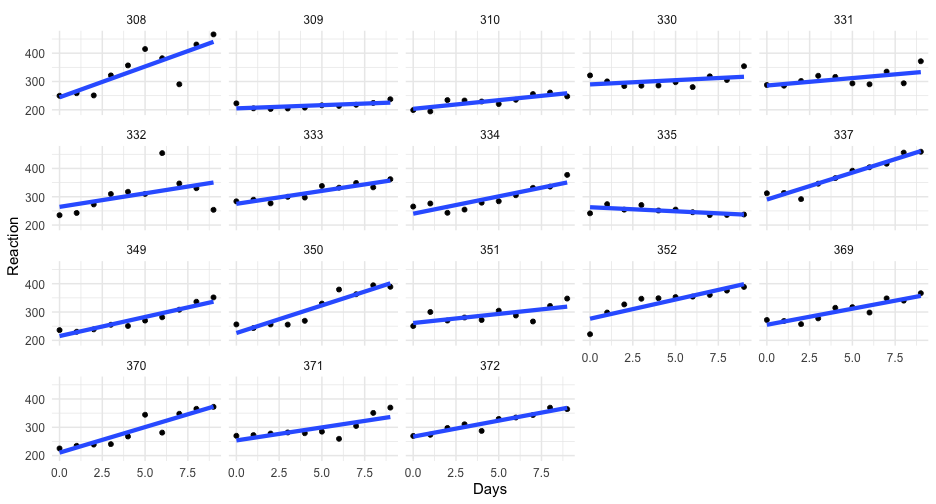
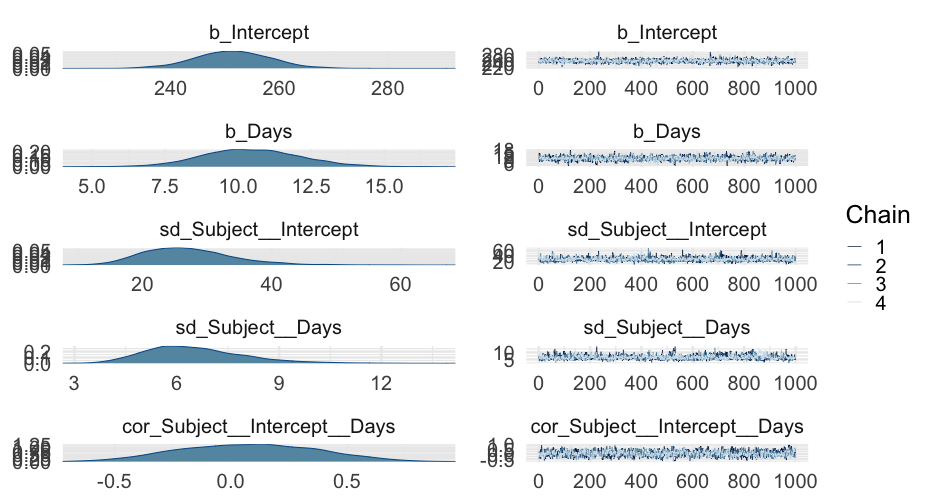
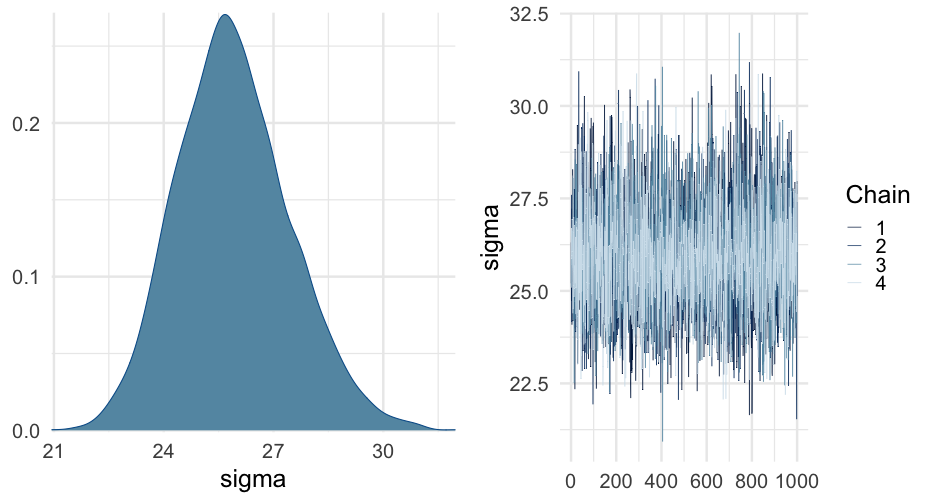
Notice the syntax is essentially equivalent to **lme4**

```r
sleep_m1 <- brm(Reaction ~ Days + (Days | Subject), data = lme4::sleepstudy)
summary(sleep_m1)
```

```
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: Reaction ~ Days + (Days | Subject) 
##    Data: lme4::sleepstudy (Number of observations: 180) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Group-Level Effects: 
## ~Subject (Number of levels: 18) 
##                     Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sd(Intercept)          27.06      7.15    15.59    42.69 1.00     1529     2353
## sd(Days)                6.55      1.49     4.19    10.04 1.00     1144     1440
## cor(Intercept,Days)     0.08      0.29    -0.47     0.64 1.01     1125     1844
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept   251.42      7.17   237.21   265.47 1.00     2093     2543
## Days         10.45      1.71     7.23    13.95 1.00     1660     2090
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma    25.91      1.54    23.13    29.17 1.00     3581     2712
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# Fixed effect
The uncertainty has increased

```r
conditional_effects(sleep_m1)
```

![](w8p1_files/figure-html/unnamed-chunk-31-1.png)

---
# Checking your model

```r
pp_check(sleep_m1)
```

![](w8p1_files/figure-html/unnamed-chunk-32-1.png)

---
# More checks

```r
plot(sleep_m1)
```

![](w8p1_files/figure-html/unnamed-chunk-33-1.png)![](w8p1_files/figure-html/unnamed-chunk-33-2.png)

---
# Even more

```r
launch_shinystan(sleep_m1)
```

---
# Model comparison

.footnote[See [here](https://arxiv.org/abs/1507.04544) for probably the best paper on this topic to date (imo)]

* Two primary (modern) methods

+ Leave-one-out Cross-Validation (LOO)
  
  + Widely Applicable Information Criterion (WAIC)

--
Both provide estimates of the *out-of-sample* predictive accuracy of the model. LOO is similar to K-fold CV, while WAIC is similar to AIC/BIC (but an improved version for Bayes models)

--
Both can be computed using **brms**. LOO is approximated (not actually refit each time).

---
# LOO: M0

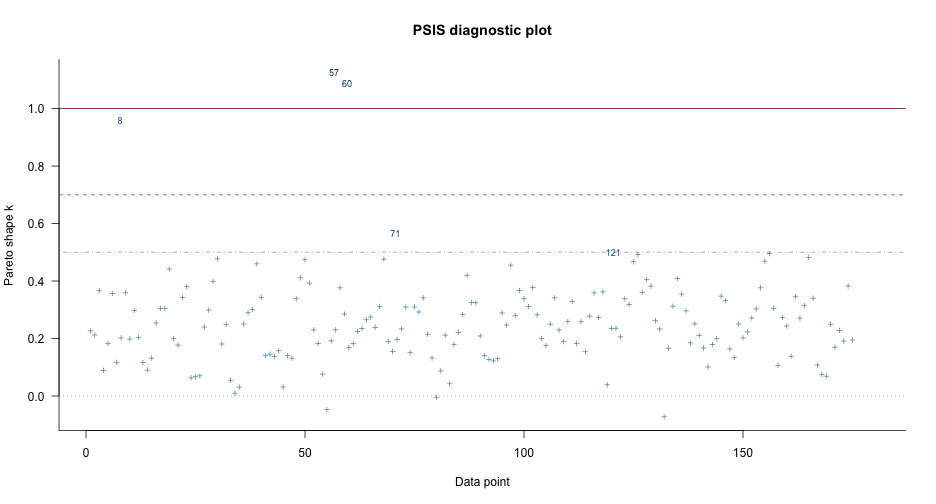
```r
loo(sleep_m0)
```

```
## 
## Computed from 4000 by 180 log-likelihood matrix
## 
##          Estimate   SE
## elpd_loo   -953.3 10.5
## p_loo         3.2  0.5
## looic      1906.5 21.0
## ------
## Monte Carlo SE of elpd_loo is 0.0.
## 
## All Pareto k estimates are good (k < 0.5).
## See help('pareto-k-diagnostic') for details.
```

---
# LOO: M1

```r
loo(sleep_m1)
```

```
## Warning: Found 3 observations with a pareto_k > 0.7 in model 'sleep_m1'. It is recommended to set 'moment_match = TRUE' in order to perform moment matching for
## problematic observations.
```

```
## 
## Computed from 4000 by 180 log-likelihood matrix
## 
##          Estimate   SE
## elpd_loo   -861.7 22.7
## p_loo        34.7  8.8
## looic      1723.3 45.5
## ------
## Monte Carlo SE of elpd_loo is NA.
## 
## Pareto k diagnostic values:
##                          Count Pct.    Min. n_eff
## (-Inf, 0.5]   (good)     175   97.2%   682       
##  (0.5, 0.7]   (ok)         2    1.1%   2189      
##    (0.7, 1]   (bad)        1    0.6%   14        
##    (1, Inf)   (very bad)   2    1.1%   9         
## See help('pareto-k-diagnostic') for details.
```

---
# Plot

```r
plot(loo(sleep_m1), label_points = TRUE)
```

```
## Warning: Found 3 observations with a pareto_k > 0.7 in model 'sleep_m1'. It is recommended to set 'moment_match = TRUE' in order to perform moment matching for
## problematic observations.
```

![](w8p1_files/figure-html/unnamed-chunk-37-1.png)

---
# Interpretation

Large values here (anything above 0.7) is an indication of model misspecification

Smaller values do not guarantee a well-specified model, however

---
# LOO Compare

.footnote[This is a fairly complicated topic, and we won't spend a lot of time on it. See [here](https://mc-stan.org/loo/articles/loo2-example.html) for a bit more information specifically on the functions]

The best fitting model will be on top. Use the standard error within your interpretation

```r
loo_compare(loo(sleep_m0), loo(sleep_m1))
```

```
## Warning: Found 3 observations with a pareto_k > 0.7 in model 'sleep_m1'. It is recommended to set 'moment_match = TRUE' in order to perform moment matching for
## problematic observations.
```

```
##          elpd_diff se_diff
## sleep_m1   0.0       0.0  
## sleep_m0 -91.6      21.4
```

---
# WAIC
Similar to other information criteria.

```r
waic(sleep_m0)
```

```
## 
## Computed from 4000 by 180 log-likelihood matrix
## 
##           Estimate   SE
## elpd_waic   -953.3 10.5
## p_waic         3.2  0.5
## waic        1906.5 21.0
```

```r
waic(sleep_m1)
```

```
## Warning: 
## 14 (7.8%) p_waic estimates greater than 0.4. We recommend trying loo instead.
```

```
## 
## Computed from 4000 by 180 log-likelihood matrix
## 
##           Estimate   SE
## elpd_waic   -860.2 22.3
## p_waic        33.2  8.4
## waic        1720.5 44.7
## 
## 14 (7.8%) p_waic estimates greater than 0.4. We recommend trying loo instead.
```

---
# Compare

You can use `waic` within `loo_compare()`

```r
loo_compare(waic(sleep_m0), waic(sleep_m1))
```

```
## Warning: 
## 14 (7.8%) p_waic estimates greater than 0.4. We recommend trying loo instead.
```

```
##          elpd_diff se_diff
## sleep_m1   0.0       0.0  
## sleep_m0 -93.0      21.0
```

---
# Another model

```r
kidney_m0 <- brm(time ~ age + sex, data = kidney)
pp_check(kidney_m0, type = "ecdf_overlay")
```

![](w8p1_files/figure-html/unnamed-chunk-43-1.png)

---
# Fixing this
We need to change the assumptions of our model - specifically that the outcome is not normally distributed

--
### Plot the raw data

```r
ggplot(kidney, aes(time)) +
  geom_histogram(alpha = 0.7)
```

![](w8p1_files/figure-html/unnamed-chunk-44-1.png)

---
# Maybe Poisson?

(I realize we haven't talked about these types of models yet)

```r
kidney_m1 <- brm(time ~ age + sex, 
                 data = kidney, 
                 family = poisson())
```

---
# Nope

```r
pp_check(kidney_m1, type = "ecdf_overlay")
```

![](w8p1_files/figure-html/unnamed-chunk-47-1.png)

---
# Gamma w/log link

```r
kidney_m2 <- brm(time ~ age + sex, 
                 data = kidney, 
                 family = Gamma("log"))
pp_check(kidney_m2, type = "ecdf_overlay")
```

![](w8p1_files/figure-html/unnamed-chunk-50-1.png)

---
# Specifying priors
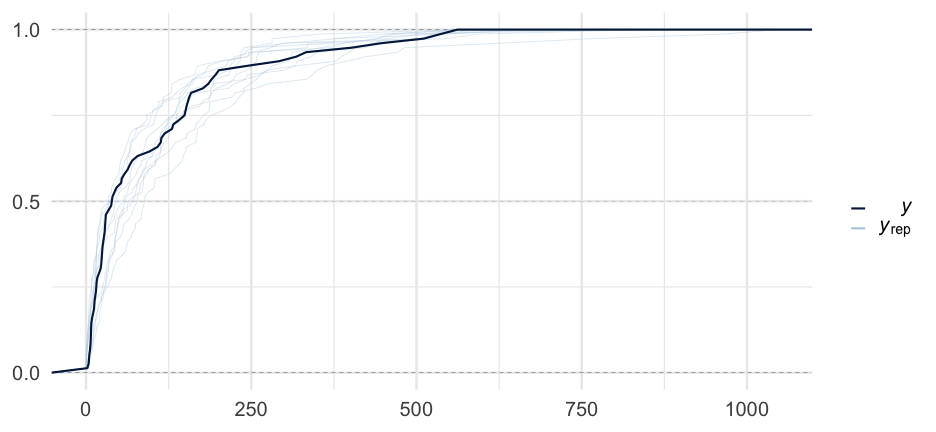
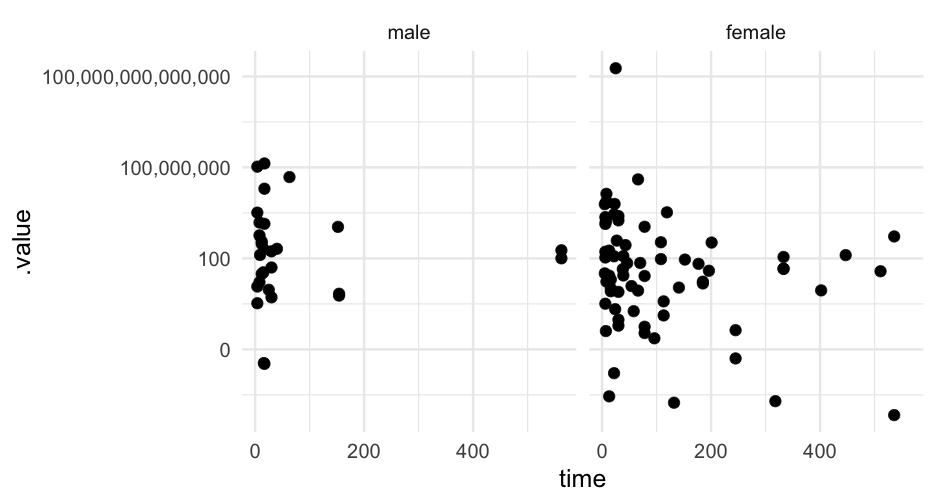
Let's sample from *only* our priors to see what kind of predictions we get.

Here, we're specifying that our beta coefficient prior is `$\beta \sim N(0, 0.5)$`

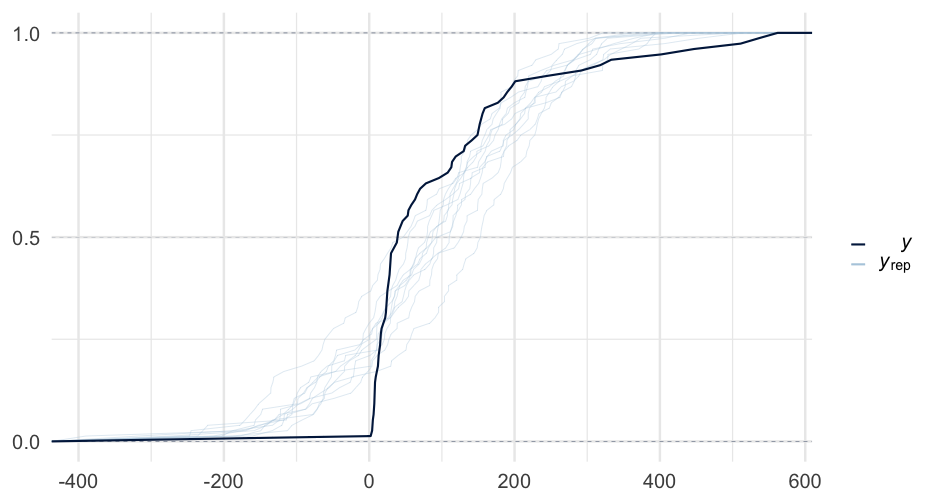
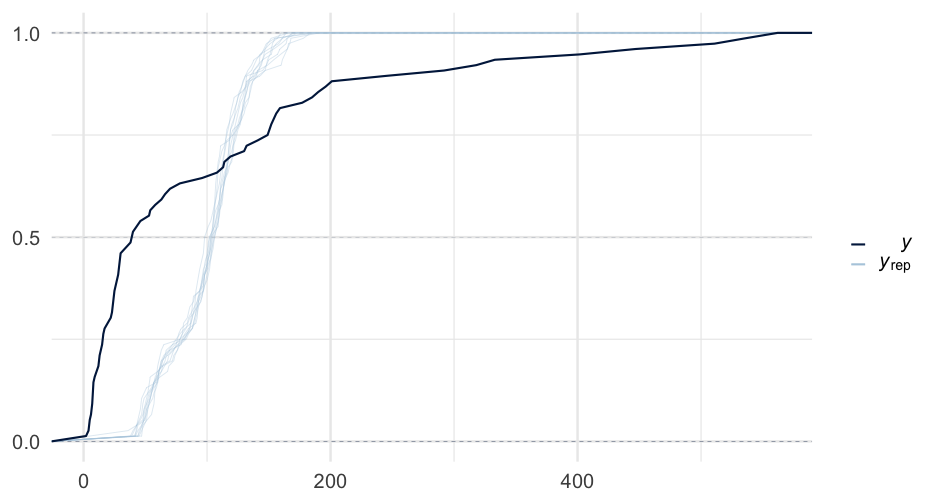
```r
kidney_m3 <- brm(
  time ~ age + sex, 
  data = kidney,
  family = Gamma("log"),
  prior = prior(normal(0, 0.5), class = "b"),
  sample_prior = "only"
)
```

---

```r
kidney_m3
```

```
## Warning: There were 2253 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-
## transitions-after-warmup
```

```
##  Family: gamma 
##   Links: mu = log; shape = identity 
## Formula: time ~ age + sex 
##    Data: kidney (Number of observations: 76) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept     4.23     22.42   -39.94    46.55 1.01      629      991
## age          -0.02      0.51    -0.97     0.97 1.01      629      946
## sexfemale     0.01      0.50    -0.98     0.97 1.01      667     1196
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## shape     0.42      3.64     0.00     2.35 1.01      436      711
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# Prior predictions
Random sample of 100 points

![](w8p1_files/figure-html/unnamed-chunk-54-1.png)

---
# Why?
It seemed like our prior was fairly tight

--
The exploding prior happens because of the log transformation

* Age is coded in years

* Imagine a coef of 1 (2 standard deviations above our prior)

* Prediction for a 25 year old would be `$\exp(25)$` = 7.2004899\times 10^{10}

---
# A note on prior specifications
* It's hard

* I don't have a ton of good advice

* Be particularly careful when you're using distributions that have anything other than an identity link (e.g., log link, as we are here)

---
# One more model
Let's fit a model we've fit previously

--
In Week 4, we fit this model

```r
library(lme4)
popular <- read_csv(here::here("data", "popularity.csv"))
m_lmer <- lmer(popular ~ extrav + (extrav|class), popular,
               control = lmerControl(optimizer = "bobyqa"))
```

--
Try fitting the same model with **{brms}** with the default, diffuse priors

---
# Bayesian verision

```r
m_brms <- brm(popular ~ extrav + (extrav|class), popular)
```

```
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: popular ~ extrav + (extrav | class) 
##    Data: popular (Number of observations: 2000) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Group-Level Effects: 
## ~class (Number of levels: 100) 
##                       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sd(Intercept)             1.72      0.17     1.41     2.08 1.00     1165     2052
## sd(extrav)                0.16      0.03     0.11     0.22 1.01      724     1755
## cor(Intercept,extrav)    -0.95      0.03    -1.00    -0.89 1.01      358      564
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept     2.46      0.20     2.06     2.84 1.00      994     1951
## extrav        0.49      0.03     0.44     0.54 1.00     1510     2474
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma     0.95      0.02     0.92     0.98 1.00     4787     2392
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# lme4 model

```r
arm::display(m_lmer)
```

```
## lmer(formula = popular ~ extrav + (extrav | class), data = popular, 
##     control = lmerControl(optimizer = "bobyqa"))
##             coef.est coef.se
## (Intercept) 2.46     0.20   
## extrav      0.49     0.03   
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  class    (Intercept) 1.73           
##           extrav      0.16     -0.97 
##  Residual             0.95           
## ---
## number of obs: 2000, groups: class, 100
## AIC = 5791.4, DIC = 5762
## deviance = 5770.7
```

---
# Add priors

* Multiple ways to do this

* Generally, I allow the intercept to just be what it is

* For "fixed" effects, you might consider [regularizing](https://vasishth.github.io/bayescogsci/book/sec-sensitivity.html#regularizing-priors) priors.

* You can also set priors for individual parameters

* In my experience, you  will mostly want to set priors for  different "class"es of parameters, e.g.: `Intercept`, `b`, `sd`, `sigma`, `cor`

---
# Half-Cauchy distribution
This is the distribution most often used for standard deviation priors
![](w8p1_files/figure-html/unnamed-chunk-60-1.png)

---
# Specify some new priors
Let's specify some regularizing priors for the fixed effects and standard deviations

```r
priors <- c(
  prior(normal(0, 0.5), class = b),
  prior(cauchy(0, 1), class = sd)
)

m_brms2 <- brm(popular ~ extrav + (extrav|class), 
               data = popular,
               prior = priors)
```

---
Almost no difference in this case

```r
m_brms2
```

```
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: popular ~ extrav + (extrav | class) 
##    Data: popular (Number of observations: 2000) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Group-Level Effects: 
## ~class (Number of levels: 100) 
##                       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sd(Intercept)             1.70      0.17     1.39     2.06 1.01     1358     1824
## sd(extrav)                0.16      0.03     0.11     0.22 1.00      871     1683
## cor(Intercept,extrav)    -0.95      0.03    -1.00    -0.88 1.01      437      871
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept     2.48      0.20     2.08     2.86 1.00     1157     1810
## extrav        0.49      0.03     0.44     0.54 1.00     1960     2642
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma     0.95      0.02     0.92     0.98 1.00     3976     2977
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# Speed
We'll never reach the `lme4::lmer()` speeds, but we can make it faster.

* Parallelize (not always as effective as you might hope)

* Use the cmdstan backend
  + This requires a little bit of additional work, but is probably worth it if you're
  fitting bigger models.

---
# Installing cmdstan

First, install the [**{cmdstanr}**](https://mc-stan.org/cmdstanr/articles/cmdstanr.html) package

```r
install.packages(
  "cmdstanr",
  repos = c(
    "https://mc-stan.org/r-packages/", 
    getOption("repos")
  )
)
```

--
Then, install **cmdstan**

```r
cmdstanr::install_cmdstan()
```

---
# Timings
I'm not evaluating the below, but the timings were 112.646, 84.561, and 42.934 seconds, respectively.

```r
library(tictoc)

tic()
m_brms <- brm(popular ~ extrav + (extrav|class), 
              data = popular)
toc()

# cmdstan
tic()
m_brms2 <- brm(popular ~ extrav + (extrav|class), 
               data = popular,
*              backend = "cmdstanr")
toc()

# cmdstan w/parallelization
tic()
m_brms3 <- brm(popular ~ extrav + (extrav|class), 
               data = popular,
               backend = "cmdstanr",
*              cores = 4)
toc()
```

---
class: inverse-red middle
# Wrapping up our Bayes intro

---
# Advantages to Bayes
* Opportunity to incorporate prior knowledge into the modeling process (you don't really *have* to - could just set wide priors)

* Natural interpretation of uncertainty

* Can often allow you to estimate models that are difficult if not impossible with frequentist methods

## Disadvatages

* Generally going to be slower in implementation

* You may run into pushback from others - particularly with respect to priors

---
# Notes on the posterior
* The posterior is the distribution of the parameters, given the data

* Think of it as the distribution of what we don't know, but are interested in (model parameters), given what we know or have observed (the data), and our prior beliefs

* Gives a complete picture of parameter uncertainty

* We can do lots of things with the posterior that is hard to get otherwise

---
class: inverse-green middle
# Break

.center[
<div class="countdown" id="timer_60b90ab2" style="right:0;bottom:0;" data-warnwhen="0">
<code class="countdown-time"><span class="countdown-digits minutes">05</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code>
</div>
]

---
class: inverse-red middle
# Review of logistic regression

---
# Data generating distribution
Up to this point, we've been assuming the data were generated from a normal distribution.

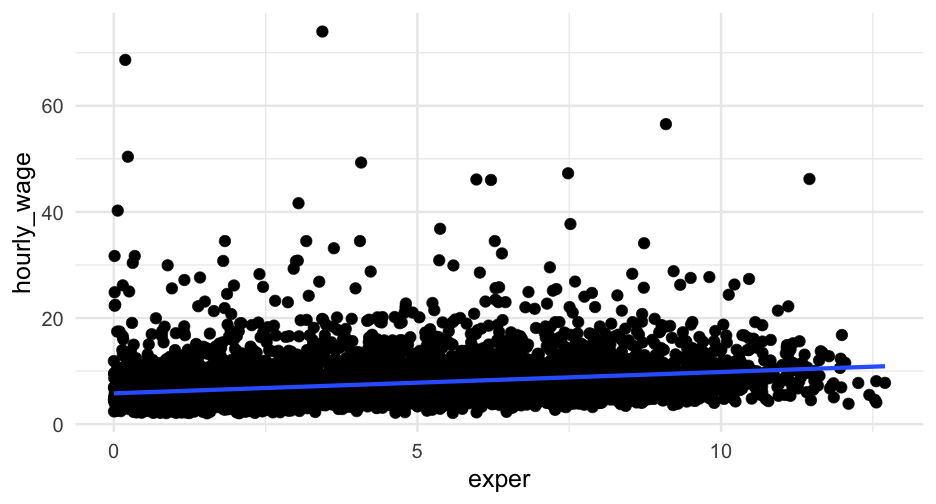
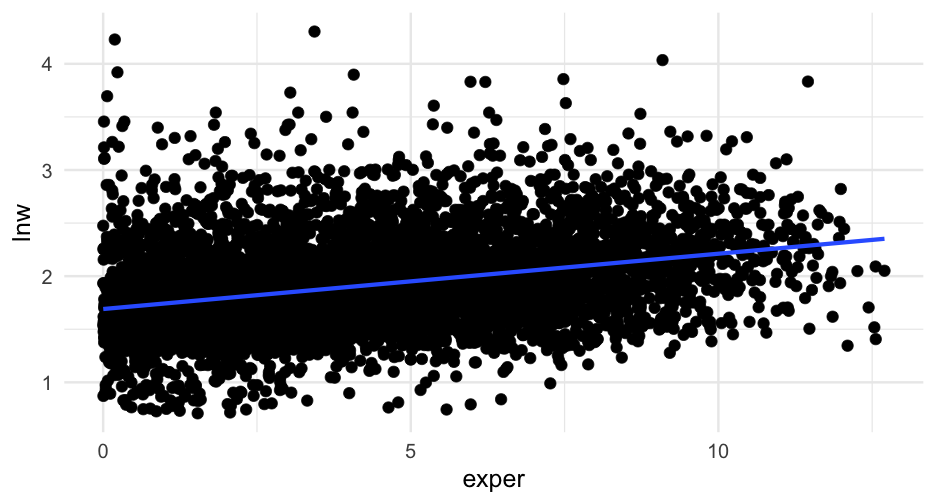
For example, we might fit a simple linear regression model to the wages data like this

$$
`\begin{aligned}
  \operatorname{wages}_{i}  &\sim N \left(\widehat{y}, \sigma^2 \right) \\
  \widehat{y} &= \alpha + \beta_{1}(\operatorname{exper})
\end{aligned}`
$$

where we're embedding a linear model into the mean

--
In code

```r
wages <- read_csv(here::here("data", "wages.csv")) %>% 
  mutate(hourly_wage = exp(lnw))

wages_lm <- lm(hourly_wage ~ exper, data = wages)
```

---
# Graphically

```r
ggplot(wages, aes(exper, hourly_wage)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)
```

![](w8p1_files/figure-html/unnamed-chunk-68-1.png)

--
Aside - you see why the log of wages was modeled instead?

---
# Log wages

```r
ggplot(wages, aes(exper, lnw)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)
```

![](w8p1_files/figure-html/unnamed-chunk-69-1.png)

---
# Move to binary model
Let's split the wages data into a binary classification based on whether it's above or below the mean.

```r
wages <- wages %>% 
  mutate(
    high_wage = ifelse(
      hourly_wage > mean(hourly_wage, na.rm = TRUE), 1, 0
    )
  )

wages %>% 
  select(id, hourly_wage, high_wage)
```

```
## # A tibble: 6,402 x 3
##       id hourly_wage high_wage
##    <dbl>       <dbl>     <dbl>
##  1    31    4.441535         0
##  2    31    4.191254         0
##  3    31    4.344888         0
##  4    31    5.748851         0
##  5    31    6.896403         0
##  6    31    5.523435         0
##  7    31    8.052640         1
##  8    31    8.406456         1
##  9    36    7.257243         0
## 10    36    6.037560         0
## # … with 6,392 more rows
```

---
# Plot

```r
means <- wages %>% 
  group_by(high_wage) %>% 
  summarize(mean = mean(exper))

ggplot(wages, aes(exper, high_wage)) +
  geom_point(alpha = 0.01) +
  geom_point(aes(x = mean), data = means, 
             shape = 23, 
             fill = "cornflowerblue")
```

![](w8p1_files/figure-html/unnamed-chunk-71-1.png)

---
# We could fit a linear model

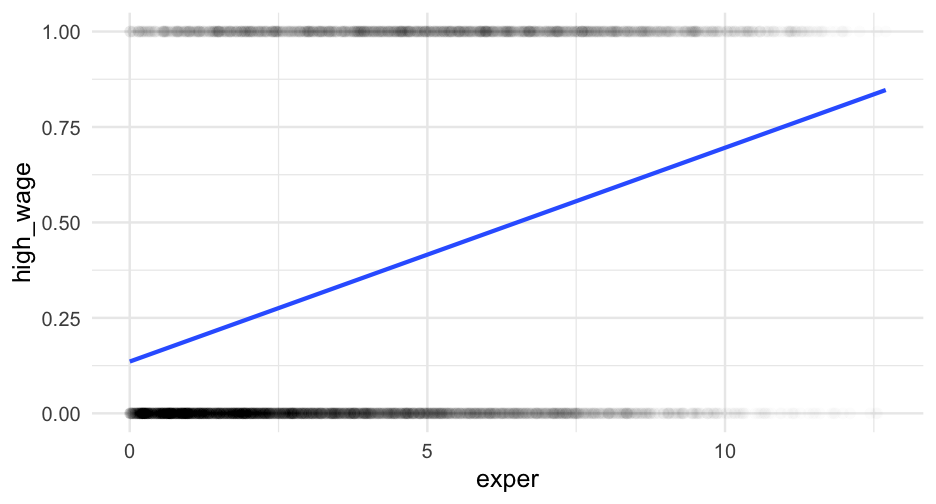
```r
m_lpm <- lm(high_wage ~ exper, data = wages)
arm::display(m_lpm)
```

```
## lm(formula = high_wage ~ exper, data = wages)
##             coef.est coef.se
## (Intercept) 0.14     0.01   
## exper       0.06     0.00   
## ---
## n = 6402, k = 2
## residual sd = 0.45, R-Squared = 0.11
```

--
This is referred to as a linear probability model (LPM) and they are pretty hotly contested, with proponents and detractors

---
# Plot

```r
ggplot(wages, aes(exper, high_wage)) +
  geom_point(alpha = 0.01) +
  geom_smooth(method = "lm", se = FALSE)
```

![](w8p1_files/figure-html/unnamed-chunk-73-1.png)

---
# Prediction

What if somebody has an experience of 25 years?

```r
predict(m_lpm, newdata = data.frame(exper = 25))
```

```
##        1 
## 1.535723
```

🤨

Our prediction goes outside the range of our data.

--
As a rule, the assumed data generating process should match the boundaries of the data.

--
Of course, you could truncate after the fact. I think that's less than ideal (see [here](https://www.alexpghayes.com/blog/consistency-and-the-linear-probability-model/) or [here](https://github.com/alexpghayes/linear-probability-model/blob/master/presentation.pdf) for discussions contrasting LPM with logistic regression).

---
# The binomial model

$$
y_i \sim \text{Binomial}(n, p_i)
$$

--
Think in terms of coin flips

--
`$n$` is the number of coin flips, while `$p_i$` is the probability of heads

---
# Example
Flip 1 coin 10 times

```r
set.seed(42)
rbinom(
  n = 10, # number of trials
  size = 1, # number of coins
  prob = 0.5 # probability of heads
)
```

```
##  [1] 1 1 0 1 1 1 1 0 1 1
```

--
Side note - a binomial model with `size = 1` (or `$n = 1$` in equation form) is equivalent to a Bernoulli distribution

Flip 10 coins 1 time

```r
rbinom(n = 1, size = 10, prob = 0.5)
```

```
## [1] 5
```

---
# Modeling
We now build a linear model for `$p$`, just like we previously built a linear model for `$\mu$`.

--
.center[
.realbig[
A problem
]
]

Probability is bounded `$[0, 1]$`

We need to ensure that our model respects these bounds

---
# Link functions

We solve this problem by using a *link* function

$$
`\begin{aligned}
y_i &\sim \text{Binomial}(n, p_i) \\
f(p_i) &= \alpha + \beta(x_i) 
\end{aligned}`
$$

--
* Instead of modeling `$p_i$` directly, we model `$f(p_i)$`

--
* The specific `$f$` is the link function

--
* Link functions map the *linear* space of the model to the *non-linear* parameters (like probability)

--
* The *log* and *logit* links are most common

---
# Binomial logistic regression
If we only have two categories, we commonly assume a binomial distribution, with a logit link.

$$
`\begin{aligned}
y_i &\sim \text{Binomial}(n, p_i) \\
\text{logit}(p_i) &= \alpha + \beta(x_i) 
\end{aligned}`
$$

--
where the logit link is defined by the *log-odds*

$$
\text{logit}(p_i) = \log\left[\frac{p_i}{1-p_i}\right]
$$

--
So

$$
\log\left[\frac{p_i}{1-p_i}\right] = \alpha + \beta(x_i) 
$$

---
# Inverse link

What we probably want to interpret is probability

We can transform the log-odds to probability by exponentiating

$$
p_i = \frac{\exp(\alpha + \beta(x_i))}{1 + \exp(\alpha + \beta(x_i))}
$$
--
This is the logistic function, or the inverse-logit.

---
# Example logistic regression model

```r
m_glm <- glm(high_wage ~ exper, 
             data = wages, 
*            family = binomial(link = "logit"))
arm::display(m_glm)
```

```
## glm(formula = high_wage ~ exper, family = binomial(link = "logit"), 
##     data = wages)
##             coef.est coef.se
## (Intercept) -1.65     0.05  
## exper        0.25     0.01  
## ---
##   n = 6402, k = 2
##   residual deviance = 7655.2, null deviance = 8345.8 (difference = 690.5)
```

---
# Coefficient interpretation
The coefficients are reported on the *log-odds* scale. Other than that, interpretation is the same.

--
For example:

The log-odds of a participant with zero years experience being in the high wage category was -1.65.

For every one year of additional experience, the log-odds of being in the high wage category increased by 0.25.

---
# Note
* Outside of scientific audiences, almost nobody is going to understand the previous slide

* You *cannot* just transform the coefficients and interpret them as probabilities (because it is non-linear on the probability scale).

---
# Log odds scale

```r
tibble(exper = 0:25) %>% 
  mutate(pred = predict(m_glm, newdata = .)) %>% 
  ggplot(aes(exper, pred)) +
  geom_line()
```

![](w8p1_files/figure-html/unnamed-chunk-78-1.png)

--
Perfectly straight line - change in log-odds are modeled as a linear function of experience

---
# Probability scale

```r
tibble(exper = 0:25) %>% 
  mutate(pred = predict(m_glm, 
                        newdata = ., 
                        type = "response")) %>% 
  ggplot(aes(exper, pred)) +
  geom_line()
```

![](w8p1_files/figure-html/unnamed-chunk-79-1.png)

--
Our model parameters map to probability non-linearly, and it is bound to `$[0, 1]$`

---
# Probability predictions

Let's make the predictions from the previous slide "by hand"

--
Recall:

$$
p_i = \frac{\exp(\alpha + \beta(x_i))}{1 + \exp(\alpha + \beta(x_i))}
$$

--
And our coefficients are

```r
coef(m_glm)
```

```
## (Intercept)       exper 
##  -1.6467568   0.2536815
```

---
# Intercept

$$
(p_i|\text{exper = 0}) = \frac{\exp(-1.65 + 0.25(0))}{1 + \exp(-1.65 + 0.25(0))}
$$

--
$$
(p_i|\text{exper = 0}) = \frac{\exp(-1.65)}{1 + \exp(-1.65)}
$$

--
$$
(p_i|\text{exper = 0}) = \frac{0.19}{1.19} = 0.16
$$

---
# Five years experience

Notice the exponentiation happens *after* adding the coefficients together

$$
(p_i|\text{exper = 5}) = \frac{\exp(-1.65 + 0.25(5))}{1 + \exp(-1.65 + 0.25(5))}
$$

--
$$
(p_i|\text{exper = 5}) = \frac{\exp(-0.4)}{1 + \exp(-0.4)}
$$

--
$$
(p_i|\text{exper = 5}) = \frac{0.67}{1.67} = 0.40
$$

---
# Fifteen years experience

$$
(p_i|\text{exper = 15}) = \frac{\exp(-1.65 + 0.25(15))}{1 + \exp(-1.65 + 0.25(15))}
$$

--
$$
(p_i|\text{exper = 15}) = \frac{\exp(2.1)}{1 + \exp(2.1)}
$$

--
$$
(p_i|\text{exper = 15}) = \frac{8.16}{9.16} = 0.89
$$

---
# More interpretation

Let's try to make this so more people might understand.

--
First, show the logistic curve on the probability scale! Can help prevent linear interpretations

--
Discuss probabilities at different `$x$` values

--
The "divide by 4" rule

---
# Divide by 4

* Logistic curve is steepest when `$p_i = 0.5$`

* The slope of the logistic curve (its derivative) is maximized at `$\beta/4$`

* Aside from the intercept, we can say that the change is *no more* than `$\beta/4$`

--
## Example

$$
\frac{0.25}{4} = 0.0625
$$

--
So, a one year increase in experience corresponds to, at most, a 6% increase in being in the high wage category

---
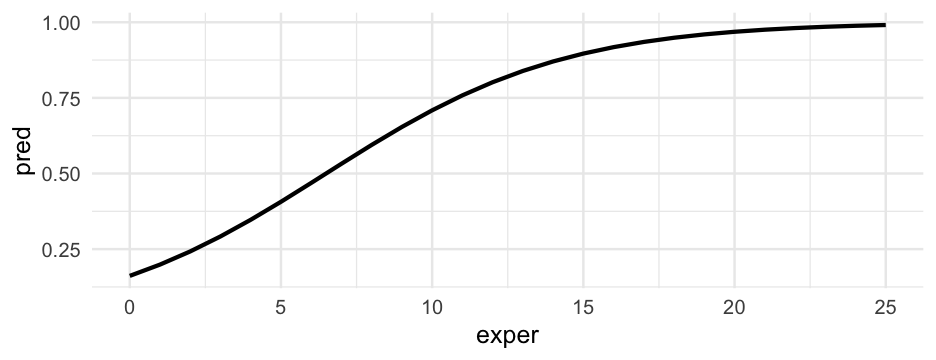
# Example writeup

There was a 16 percent chance that a participant with zero years experience would be in the *high wage* category. The logistic function, which mapped years of experience to the  probability of being in the *high-wage* category, was non-linear, as shown in Figure 1. At its steepest point, a one year increase in experience corresponded with approximately a 6% increase in the probability of being in the high-wage category. For individuals with 5, 10, and 15 years of experience, the probability increased to a 41, 71, and 90 percent chance, respectively.

---
class: inverse-red middle
# Other distributions

---
background-image: url(img/distributions.png)
background-size: contain

.footnote[Figure from [McElreath](https://xcelab.net/rm/statistical-rethinking/)]

---
class: inverse-blue middle

# Multilevel logistic regression

---
# The data
Polling data from the 1988 election.

```r
polls <- rio::import(here::here("data", "polls.dta"),
                     setclass = "tbl_df")
polls
```

```
## # A tibble: 13,544 x 10
##      org  year survey  bush state   edu   age female black weight
##    <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>  <dbl>
##  1     1     1      1     1     7     2     2      1     0   1403
##  2     1     1      1     1    33     4     3      0     0    778
##  3     1     1      1     0    20     2     1      1     0   1564
##  4     1     1      1     1    31     3     2      1     0   1055
##  5     1     1      1     1    18     3     1      1     0   1213
##  6     1     1      1     1    31     4     2      0     0    910
##  7     1     1      1     1    40     1     3      0     0    735
##  8     1     1      1     1    33     4     2      1     0    410
##  9     1     1      1     0    22     4     2      1     0    410
## 10     1     1      1     1    22     4     3      0     0    778
## # … with 13,534 more rows
```

---
# About the data

* Collected one week before the election

* Nationally representative sample

* Should use post-stratification to control for non-response, but we'll hold off on that for now (See Gelman & Hill, Chapter 14 for more details)

---
# Baseline probability

Let's assume we want to estimate the probability that Bush will be elected.

--
We could fit a single level model like this

---
# In code

Can you write the code for the previous model?

```r
bush_sl <- glm(bush ~ 1, 
               data = polls,
               family = binomial(link = "logit"))
```

```r
arm::display(bush_sl)
```

```
## glm(formula = bush ~ 1, family = binomial(link = "logit"), data = polls)
##             coef.est coef.se
## (Intercept) 0.25     0.02   
## ---
##   n = 11566, k = 1
##   residual deviance = 15858.1, null deviance = 15858.1 (difference = 0.0)
```

--
So, `$p_i = \frac{\exp(0.25)}{1 + \exp(0.25)} = 0.56$`

---
# State-level variability

To estimate state-level variability, we just specify a distribution for the intercept variability.

$$
`\begin{aligned}
\operatorname{bush} &\sim \text{Binomial}\left(n = 1, \operatorname{prob}_{\operatorname{bush} = \operatorname{1}}= \hat{P}\right) \\
 \log\left[ \frac { \hat{P} }{ 1 - \hat{P} } \right] 
 &= \alpha_{j[i]} \\
    \alpha_{j}  &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right)
    \text{, for state j = 1,} \dots \text{,J}
\end{aligned}`
$$

--
Notice we're still specifying that the intercept variability is generated by a *normal* distribution.

--
What does this variability actually represent?

--
Variance in the log-odds

---
# Fitting the model

If we're using **{lme4}**, we just swap `lmer()` for `glmer()` and specify the family and link function.

```r
library(lme4)

m0 <- glmer(bush ~ 1 + (1|state),
           data = polls,
           family = binomial(link = "logit"))
arm::display(m0)
```

```
## glmer(formula = bush ~ 1 + (1 | state), data = polls, family = binomial(link = "logit"))
## coef.est  coef.se 
##     0.25     0.06 
## 
## Error terms:
##  Groups   Name        Std.Dev.
##  state    (Intercept) 0.34    
##  Residual             1.00    
## ---
## number of obs: 11566, groups: state, 49
## AIC = 15697, DIC = 15450.4
## deviance = 15571.7
```

---
# Interpretation

* The average log odds of supporting bush was 0.25

* This average varied between states with a standard deviation of 0.34

---
# State-level variation

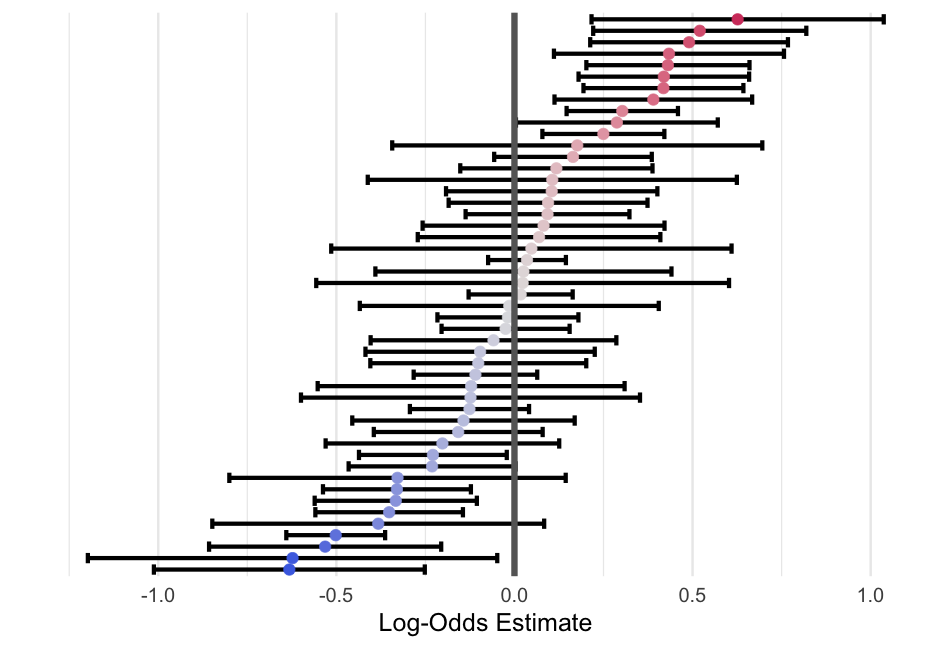
```r
library(broom.mixed)
m0_tidied <- tidy(m0, effects = "ran_vals", conf.int = TRUE)
m0_tidied
```

```
## # A tibble: 49 x 8
##    effect   group level term           estimate  std.error    conf.low   conf.high
##    <chr>    <chr> <chr> <chr>             <dbl>      <dbl>       <dbl>       <dbl>
##  1 ran_vals state 1     (Intercept)  0.5201836  0.1526301   0.2210341   0.8193332 
##  2 ran_vals state 3     (Intercept)  0.09438107 0.1424292  -0.1847750   0.3735371 
##  3 ran_vals state 4     (Intercept)  0.06905650 0.1737493  -0.2714859   0.4095989 
##  4 ran_vals state 5     (Intercept)  0.03522421 0.05570977 -0.07396493  0.1444133 
##  5 ran_vals state 6     (Intercept)  0.1045418  0.1513626  -0.1921233   0.4012070 
##  6 ran_vals state 7     (Intercept) -0.1015410  0.1546380  -0.4046260   0.2015440 
##  7 ran_vals state 8     (Intercept) -0.3824312  0.2376744  -0.8482644   0.08340195
##  8 ran_vals state 9     (Intercept) -0.6229779  0.2931982  -1.197636   -0.04832002
##  9 ran_vals state 10    (Intercept)  0.3027001  0.07975137  0.1463903   0.4590099 
## 10 ran_vals state 11    (Intercept)  0.09282107 0.1173420  -0.1371651   0.3228072 
## # … with 39 more rows
```

---
# Fancified Plot Code

```r
m0_tidied %>% 
  mutate(level = forcats::fct_reorder(level, estimate)) %>% 
  ggplot(aes(estimate, level)) +
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high)) +
  geom_point(aes(color = estimate)) +
  geom_vline(xintercept = 0, color = "gray40", size = 3) +
  labs(x = "Log-Odds Estimate", y = "") +
  colorspace::scale_color_continuous_diverging(palette = "Blue-Red 2") +
  guides(color = "none") +
  theme(panel.grid.major.y = element_blank(),
        axis.text.y = element_blank())
```

---
# Fancified Plot
![](w8p1_files/figure-html/unnamed-chunk-87-1.png)

---
# Extending the model

Let's add some predictors

* Include `age`, `female` and `black` as fixed effect predictors.

--
* We should center age so the intercept represents the sample average age.

--
You try first

---

```r
polls <- polls %>% 
  mutate(age_c = age - mean(age, na.rm = TRUE))

m1 <- glmer(bush ~ age_c + female + black + (1|state),
            data = polls,
            family = binomial(link = "logit"))
arm::display(m1)
```

```
## glmer(formula = bush ~ age_c + female + black + (1 | state), 
##     data = polls, family = binomial(link = "logit"))
##             coef.est coef.se
## (Intercept)  0.43     0.07  
## age_c       -0.08     0.02  
## female      -0.11     0.04  
## black       -1.84     0.09  
## 
## Error terms:
##  Groups   Name        Std.Dev.
##  state    (Intercept) 0.41    
##  Residual             1.00    
## ---
## number of obs: 11566, groups: state, 49
## AIC = 15137.1, DIC = 14856.7
## deviance = 14991.9
```

---
# Varying slopes
The average probability of a respondent who was coded `black == 1` who was the average age and non-female supporting Bush was

$$
\small
`\begin{equation}
(p_i|\text{age} = 0, \text{female} = 0, \text{black} = 1) = \frac{\exp(0.43 + (-0.08 \times 0) + (-0.11 \times 0) + (-1.84 \times 1))}{1 + \exp(0.43 + (-0.08 \times 0) + (-0.11 \times 0) + (-1.84 \times 1))}
\end{equation}`
$$

--
$$
(p_i|\text{age} = 0, \text{female} = 0, \text{black} = 1) = \frac{\exp(0.43 -1.84))}{1 + \exp(0.43  -1.84)}
$$

--
$$
(p_i|\text{age} = 0, \text{female} = 0, \text{black} = 1) = \frac{\exp(-1.41))}{1 + \exp(-1.41)}
$$

--
$$
(p_i|\text{age} = 0, \text{female} = 0, \text{black} = 1) = \frac{0.24}{1.24}
$$

--
$$
(p_i|\text{age} = 0, \text{female} = 0, \text{black} = 1) = 0.19
$$

---
# Vary by state?
You try first - try to fit a model that estimates between-state variability in the relation between individuals coded `black`, and their probability of voting for Bush.

```r
m2 <- glmer(bush ~ age_c + female + black + (black|state),
            data = polls,
            family = binomial(link = "logit"))
arm::display(m2)
```

```
## glmer(formula = bush ~ age_c + female + black + (black | state), 
##     data = polls, family = binomial(link = "logit"))
##             coef.est coef.se
## (Intercept)  0.43     0.07  
## age_c       -0.08     0.02  
## female      -0.11     0.04  
## black       -1.66     0.19  
## 
## Error terms:
##  Groups   Name        Std.Dev. Corr  
##  state    (Intercept) 0.44           
##           black       0.87     -0.46 
##  Residual             1.00           
## ---
## number of obs: 11566, groups: state, 49
## AIC = 15100.6, DIC = 14697.4
## deviance = 14892.0
```

---
# Look at random effects

```r
ranef_m2 <- tidy(m2, effects = "ran_vals", conf.int = TRUE) %>% 
  arrange(level)
ranef_m2
```

```
## # A tibble: 98 x 8
##    effect   group level term           estimate  std.error    conf.low conf.high
##    <chr>    <chr> <chr> <chr>             <dbl>      <dbl>       <dbl>     <dbl>
##  1 ran_vals state 1     (Intercept)  0.4768807  0.1716175   0.1405165  0.8132448
##  2 ran_vals state 1     black        1.066314   0.4118905   0.2590240  1.873605 
##  3 ran_vals state 10    (Intercept)  0.3000900  0.08425460  0.1349540  0.4652259
##  4 ran_vals state 10    black       -0.1573061  0.3564817  -0.8559974  0.5413852
##  5 ran_vals state 11    (Intercept)  0.2440973  0.1326607  -0.01591285 0.5041074
##  6 ran_vals state 11    black       -0.6672948  0.4129706  -1.476702   0.1421127
##  7 ran_vals state 13    (Intercept) -0.2406066  0.2710096  -0.7717756  0.2905624
##  8 ran_vals state 13    black        0.2180487  0.8103377  -1.370184   1.806281 
##  9 ran_vals state 14    (Intercept) -0.04190335 0.09568848 -0.2294493  0.1456426
## 10 ran_vals state 14    black       -0.3926602  0.3611247  -1.100452   0.3151311
## # … with 88 more rows
```

---
# Include fixed effects

```r
fe <- data.frame(
  fixed = fixef(m2),
  term = names(fixef(m2))
)
fe
```

```
##                   fixed        term
## (Intercept)  0.43434106 (Intercept)
## age_c       -0.08284379       age_c
## female      -0.10836146      female
## black       -1.66095113       black
```

```r
ranef_m2 <- left_join(ranef_m2, fe)
ranef_m2 %>% 
  select(level, term, estimate, fixed)
```

```
## # A tibble: 98 x 4
##    level term           estimate      fixed
##    <chr> <chr>             <dbl>      <dbl>
##  1 1     (Intercept)  0.4768807   0.4343411
##  2 1     black        1.066314   -1.660951 
##  3 10    (Intercept)  0.3000900   0.4343411
##  4 10    black       -0.1573061  -1.660951 
##  5 11    (Intercept)  0.2440973   0.4343411
##  6 11    black       -0.6672948  -1.660951 
##  7 13    (Intercept) -0.2406066   0.4343411
##  8 13    black        0.2180487  -1.660951 
##  9 14    (Intercept) -0.04190335  0.4343411
## 10 14    black       -0.3926602  -1.660951 
## # … with 88 more rows
```

---
# Add in fixed effects

```r
ranef_m2 <- ranef_m2 %>% 
  mutate(estimate = estimate + fixed)
ranef_m2
```

```
## # A tibble: 98 x 9
##    effect   group level term          estimate  std.error    conf.low conf.high      fixed
##    <chr>    <chr> <chr> <chr>            <dbl>      <dbl>       <dbl>     <dbl>      <dbl>
##  1 ran_vals state 1     (Intercept)  0.9112217 0.1716175   0.1405165  0.8132448  0.4343411
##  2 ran_vals state 1     black       -0.5946367 0.4118905   0.2590240  1.873605  -1.660951 
##  3 ran_vals state 10    (Intercept)  0.7344310 0.08425460  0.1349540  0.4652259  0.4343411
##  4 ran_vals state 10    black       -1.818257  0.3564817  -0.8559974  0.5413852 -1.660951 
##  5 ran_vals state 11    (Intercept)  0.6784383 0.1326607  -0.01591285 0.5041074  0.4343411
##  6 ran_vals state 11    black       -2.328246  0.4129706  -1.476702   0.1421127 -1.660951 
##  7 ran_vals state 13    (Intercept)  0.1937344 0.2710096  -0.7717756  0.2905624  0.4343411
##  8 ran_vals state 13    black       -1.442902  0.8103377  -1.370184   1.806281  -1.660951 
##  9 ran_vals state 14    (Intercept)  0.3924377 0.09568848 -0.2294493  0.1456426  0.4343411
## 10 ran_vals state 14    black       -2.053611  0.3611247  -1.100452   0.3151311 -1.660951 
## # … with 88 more rows
```

---
# Compute log-odds
Compute means for each group - i.e., add the coefficients

```r
to_plot <- ranef_m2 %>% 
  group_by(level) %>% 
  mutate(estimate = cumsum(estimate)) %>% 
  ungroup()

to_plot
```

```
## # A tibble: 98 x 9
##    effect   group level term          estimate  std.error    conf.low conf.high      fixed
##    <chr>    <chr> <chr> <chr>            <dbl>      <dbl>       <dbl>     <dbl>      <dbl>
##  1 ran_vals state 1     (Intercept)  0.9112217 0.1716175   0.1405165  0.8132448  0.4343411
##  2 ran_vals state 1     black        0.3165850 0.4118905   0.2590240  1.873605  -1.660951 
##  3 ran_vals state 10    (Intercept)  0.7344310 0.08425460  0.1349540  0.4652259  0.4343411
##  4 ran_vals state 10    black       -1.083826  0.3564817  -0.8559974  0.5413852 -1.660951 
##  5 ran_vals state 11    (Intercept)  0.6784383 0.1326607  -0.01591285 0.5041074  0.4343411
##  6 ran_vals state 11    black       -1.649808  0.4129706  -1.476702   0.1421127 -1.660951 
##  7 ran_vals state 13    (Intercept)  0.1937344 0.2710096  -0.7717756  0.2905624  0.4343411
##  8 ran_vals state 13    black       -1.249168  0.8103377  -1.370184   1.806281  -1.660951 
##  9 ran_vals state 14    (Intercept)  0.3924377 0.09568848 -0.2294493  0.1456426  0.4343411
## 10 ran_vals state 14    black       -1.661174  0.3611247  -1.100452   0.3151311 -1.660951 
## # … with 88 more rows
```

---
# Create factor level

```r
lev_order <- to_plot %>% 
  filter(term == "(Intercept)") %>% 
  mutate(lev = forcats::fct_reorder(level, estimate))

to_plot <- to_plot %>% 
  mutate(level = factor(level, levels = levels(lev_order$lev)))
```

---
# Plot

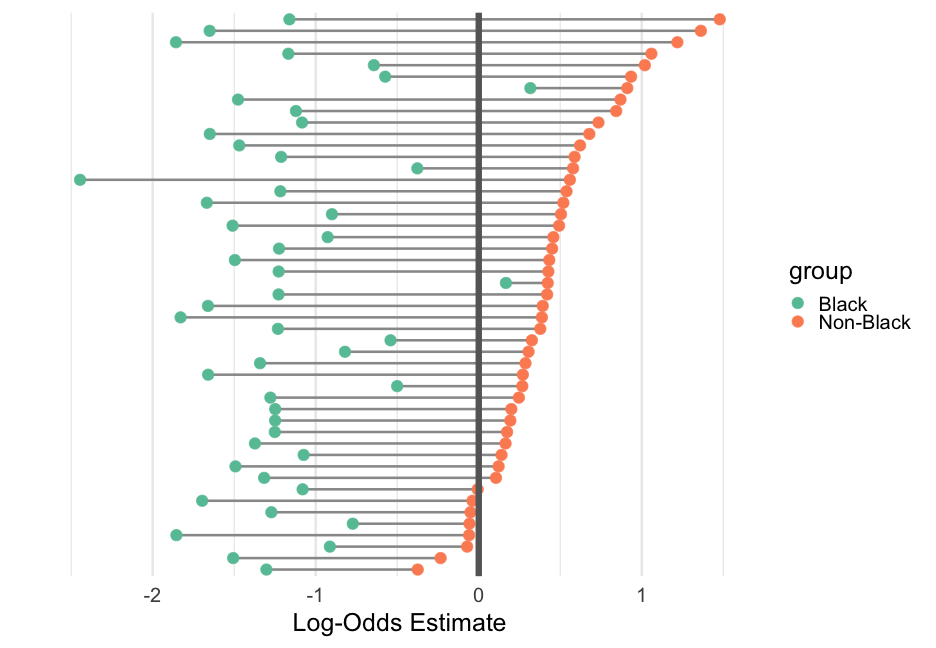
```r
# data transform
to_plot %>% 
  mutate(group = ifelse(term == "(Intercept)", "Non-Black", "Black")) %>%
  
  # plot
  ggplot(aes(estimate, level)) +
  geom_line(aes(group = level), color = "gray60", size = 1.2) +
  geom_point(aes(color = group)) +
  geom_vline(xintercept = 0.5, color = "gray40", size = 3) +
  
  # themeing stuff
  labs(x = "Probability Estimate", y = "") +
  xlim(0, 1) +
  scale_color_brewer(palette = "Set2") +
  theme(panel.grid.major.y = element_blank(),
        axis.text.y = element_blank())
```

---
# Plot
![](w8p1_files/figure-html/unnamed-chunk-96-1.png)

---
# Probability scale

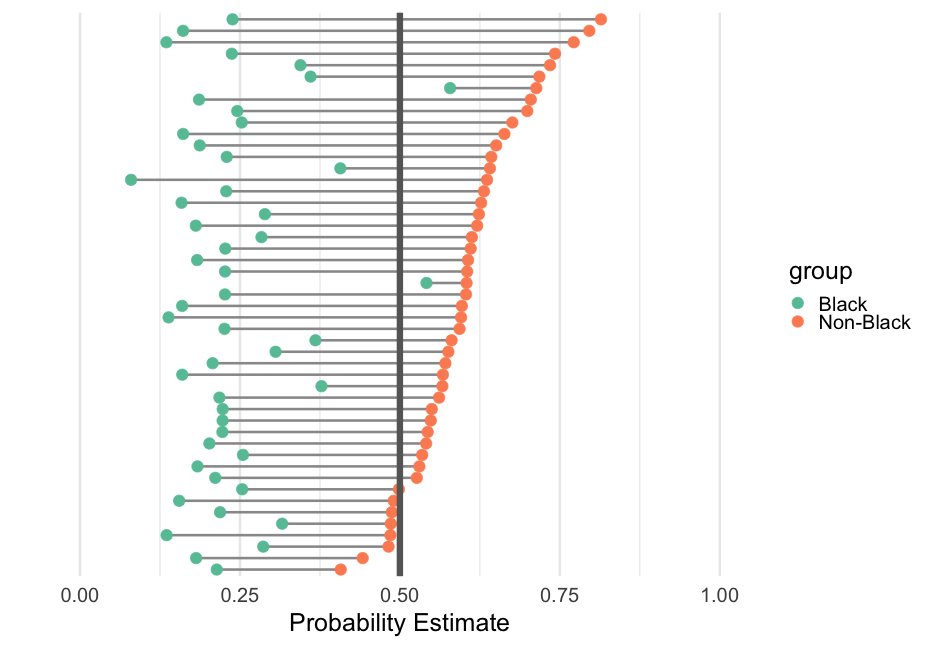
```r
# data transform
to_plot %>% 
  mutate(
    group = ifelse(term == "(Intercept)", "Non-Black", "Black"),
*   prob = exp(estimate)/(1 + exp(estimate))
  ) %>%
  
  # plot
  ggplot(aes(prob, level)) +
  geom_line(aes(group = level), color = "gray60", size = 1.2) +
  geom_point(aes(color = group)) +
  geom_vline(xintercept = 0.5, color = "gray40", size = 3) +
  
  # themeing stuff
  labs(x = "Probability Estimate", y = "") +
  xlim(0, 1) +
  scale_color_brewer(palette = "Set2") +
  theme(panel.grid.major.y = element_blank(),
        axis.text.y = element_blank())
```

---
# Probability scale

![](w8p1_files/figure-html/unnamed-chunk-98-1.png)

---
class: inverse-blue middle

# Bayes

---
# Refit
Can you fit the same model we just fit, but with **{brms}**?

You try first

Feel free to just use flat priors

---
# Flat priors

```r
library(brms)
m2_brms <- brm(bush ~ age + female + black + (black|state),
            data = polls,
            family = bernoulli(link = "logit"),
            backend = "cmdstan",
            cores = 4)
```

```
## Warning: Rows containing NAs were excluded from the model.
```

```
## 
-

Running MCMC with 4 parallel chains...
## 
## Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
## Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
## Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
## Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
## Chain 2 Iteration:  100 / 2000 [  5%]  (Warmup) 
## Chain 4 Iteration:  100 / 2000 [  5%]  (Warmup) 
## Chain 1 Iteration:  100 / 2000 [  5%]  (Warmup) 
## Chain 3 Iteration:  100 / 2000 [  5%]  (Warmup) 
## Chain 2 Iteration:  200 / 2000 [ 10%]  (Warmup) 
## Chain 4 Iteration:  200 / 2000 [ 10%]  (Warmup) 
## Chain 1 Iteration:  200 / 2000 [ 10%]  (Warmup) 
## Chain 3 Iteration:  200 / 2000 [ 10%]  (Warmup) 
## Chain 2 Iteration:  300 / 2000 [ 15%]  (Warmup) 
## Chain 4 Iteration:  300 / 2000 [ 15%]  (Warmup) 
## Chain 1 Iteration:  300 / 2000 [ 15%]  (Warmup) 
## Chain 2 Iteration:  400 / 2000 [ 20%]  (Warmup) 
## Chain 3 Iteration:  300 / 2000 [ 15%]  (Warmup) 
## Chain 4 Iteration:  400 / 2000 [ 20%]  (Warmup) 
## Chain 1 Iteration:  400 / 2000 [ 20%]  (Warmup) 
## Chain 2 Iteration:  500 / 2000 [ 25%]  (Warmup) 
## Chain 3 Iteration:  400 / 2000 [ 20%]  (Warmup) 
## Chain 4 Iteration:  500 / 2000 [ 25%]  (Warmup) 
## Chain 2 Iteration:  600 / 2000 [ 30%]  (Warmup) 
## Chain 1 Iteration:  500 / 2000 [ 25%]  (Warmup) 
## Chain 3 Iteration:  500 / 2000 [ 25%]  (Warmup) 
## Chain 4 Iteration:  600 / 2000 [ 30%]  (Warmup) 
## Chain 2 Iteration:  700 / 2000 [ 35%]  (Warmup) 
## Chain 1 Iteration:  600 / 2000 [ 30%]  (Warmup) 
## Chain 3 Iteration:  600 / 2000 [ 30%]  (Warmup) 
## Chain 4 Iteration:  700 / 2000 [ 35%]  (Warmup) 
## Chain 2 Iteration:  800 / 2000 [ 40%]  (Warmup) 
## Chain 1 Iteration:  700 / 2000 [ 35%]  (Warmup) 
## Chain 3 Iteration:  700 / 2000 [ 35%]  (Warmup) 
## Chain 4 Iteration:  800 / 2000 [ 40%]  (Warmup) 
## Chain 2 Iteration:  900 / 2000 [ 45%]  (Warmup) 
## Chain 1 Iteration:  800 / 2000 [ 40%]  (Warmup) 
## Chain 3 Iteration:  800 / 2000 [ 40%]  (Warmup) 
## Chain 4 Iteration:  900 / 2000 [ 45%]  (Warmup) 
## Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
## Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
## Chain 1 Iteration:  900 / 2000 [ 45%]  (Warmup) 
## Chain 3 Iteration:  900 / 2000 [ 45%]  (Warmup) 
## Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
## Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
## Chain 2 Iteration: 1100 / 2000 [ 55%]  (Sampling) 
## Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
## Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
## Chain 4 Iteration: 1100 / 2000 [ 55%]  (Sampling) 
## Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
## Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
## Chain 2 Iteration: 1200 / 2000 [ 60%]  (Sampling) 
## Chain 1 Iteration: 1100 / 2000 [ 55%]  (Sampling) 
## Chain 4 Iteration: 1200 / 2000 [ 60%]  (Sampling) 
## Chain 2 Iteration: 1300 / 2000 [ 65%]  (Sampling) 
## Chain 3 Iteration: 1100 / 2000 [ 55%]  (Sampling) 
## Chain 1 Iteration: 1200 / 2000 [ 60%]  (Sampling) 
## Chain 4 Iteration: 1300 / 2000 [ 65%]  (Sampling) 
## Chain 2 Iteration: 1400 / 2000 [ 70%]  (Sampling) 
## Chain 1 Iteration: 1300 / 2000 [ 65%]  (Sampling) 
## Chain 3 Iteration: 1200 / 2000 [ 60%]  (Sampling) 
## Chain 4 Iteration: 1400 / 2000 [ 70%]  (Sampling) 
## Chain 2 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
## Chain 1 Iteration: 1400 / 2000 [ 70%]  (Sampling) 
## Chain 4 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
## Chain 2 Iteration: 1600 / 2000 [ 80%]  (Sampling) 
## Chain 3 Iteration: 1300 / 2000 [ 65%]  (Sampling) 
## Chain 1 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
## Chain 4 Iteration: 1600 / 2000 [ 80%]  (Sampling) 
## Chain 2 Iteration: 1700 / 2000 [ 85%]  (Sampling) 
## Chain 1 Iteration: 1600 / 2000 [ 80%]  (Sampling) 
## Chain 3 Iteration: 1400 / 2000 [ 70%]  (Sampling) 
## Chain 4 Iteration: 1700 / 2000 [ 85%]  (Sampling) 
## Chain 2 Iteration: 1800 / 2000 [ 90%]  (Sampling) 
## Chain 1 Iteration: 1700 / 2000 [ 85%]  (Sampling) 
## Chain 4 Iteration: 1800 / 2000 [ 90%]  (Sampling) 
## Chain 3 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
## Chain 2 Iteration: 1900 / 2000 [ 95%]  (Sampling) 
## Chain 1 Iteration: 1800 / 2000 [ 90%]  (Sampling) 
## Chain 4 Iteration: 1900 / 2000 [ 95%]  (Sampling) 
## Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling) 
## Chain 2 finished in 41.0 seconds.
## Chain 1 Iteration: 1900 / 2000 [ 95%]  (Sampling) 
## Chain 3 Iteration: 1600 / 2000 [ 80%]  (Sampling) 
## Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling) 
## Chain 4 finished in 41.9 seconds.
## Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
## Chain 1 finished in 42.7 seconds.
## Chain 3 Iteration: 1700 / 2000 [ 85%]  (Sampling) 
## Chain 3 Iteration: 1800 / 2000 [ 90%]  (Sampling) 
## Chain 3 Iteration: 1900 / 2000 [ 95%]  (Sampling) 
## Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling) 
## Chain 3 finished in 48.2 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 43.5 seconds.
## Total execution time: 48.7 seconds.
```

---
# Model summary

```r
summary(m2_brms)
```

```
##  Family: bernoulli 
##   Links: mu = logit 
## Formula: bush ~ age + female + black + (black | state) 
##    Data: polls (Number of observations: 11566) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Group-Level Effects: 
## ~state (Number of levels: 49) 
##                      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sd(Intercept)            0.46      0.06     0.36     0.59 1.00      949     2013
## sd(black)                0.96      0.20     0.61     1.41 1.01     1202     2403
## cor(Intercept,black)    -0.40      0.19    -0.71     0.02 1.00     1417     2354
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept     0.62      0.09     0.46     0.80 1.00      732     1254
## age          -0.08      0.02    -0.12    -0.05 1.00     5674     3257
## female       -0.11      0.04    -0.19    -0.03 1.00     5243     2793
## black        -1.67      0.22    -2.10    -1.24 1.00     1050     1688
## 
## Samples were drawn using sample(hmc). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
```

---
# Posterior predictive check

```r
pp_check(m2_brms, type = "bars")
```

![](w8p1_files/figure-html/unnamed-chunk-101-1.png)

---
# Posterior predictive check 2

```r
pp_check(m2_brms, type = "stat")
```

![](w8p1_files/figure-html/unnamed-chunk-102-1.png)

---
class: inverse-green middle
# Next time
* More Bayes for binomial logistic regression
* Plotting Bayes models
* Missing data 
* Piece-wise growth models